문제 출처: https://programmers.co.kr/learn/courses/30/lessons/42861
문제 설명
n개의 섬 사이에 다리를 건설하는 비용(costs)이 주어질 때, 최소의 비용으로 모든 섬이 서로 통행 가능하도록 만들 때 필요한 최소 비용을 return 하도록 solution을 완성하세요.
다리를 여러 번 건너더라도, 도달할 수만 있으면 통행 가능하다고 봅니다. 예를 들어 A 섬과 B 섬 사이에 다리가 있고, B 섬과 C 섬 사이에 다리가 있으면 A 섬과 C 섬은 서로 통행 가능합니다.
제한사항
-
섬의 개수 n은 1 이상 100 이하입니다.
-
costs의 길이는 ((n-1) * n) / 2이하입니다.
-
임의의 i에 대해, costs[i][0] 와 costs[i][1]에는 다리가 연결되는 두 섬의 번호가 들어있고, costs[i][2]에는 이 두 섬을 연결하는 다리를 건설할 때 드는 비용입니다.
-
같은 연결은 두 번 주어지지 않습니다. 또한 순서가 바뀌더라도 같은 연결로 봅니다. 즉 0과 1 사이를 연결하는 비용이 주어졌을 때, 1과 0의 비용이 주어지지 않습니다.
-
모든 섬 사이의 다리 건설 비용이 주어지지 않습니다. 이 경우, 두 섬 사이의 건설이 불가능한 것으로 봅니다.
연결할 수 없는 섬은 주어지지 않습니다.
예제 입력
n = 4, costs = [[0,1,1],[0,2,2],[1,2,5],[1,3,1],[2,3,8]]
예제 출력
4
입출력 예 설명
costs를 그림으로 표현하면 다음과 같으며, 이때 초록색 경로로 연결하는 것이 가장 적은 비용으로 모두를 통행할 수 있도록 만드는 방법입니다.
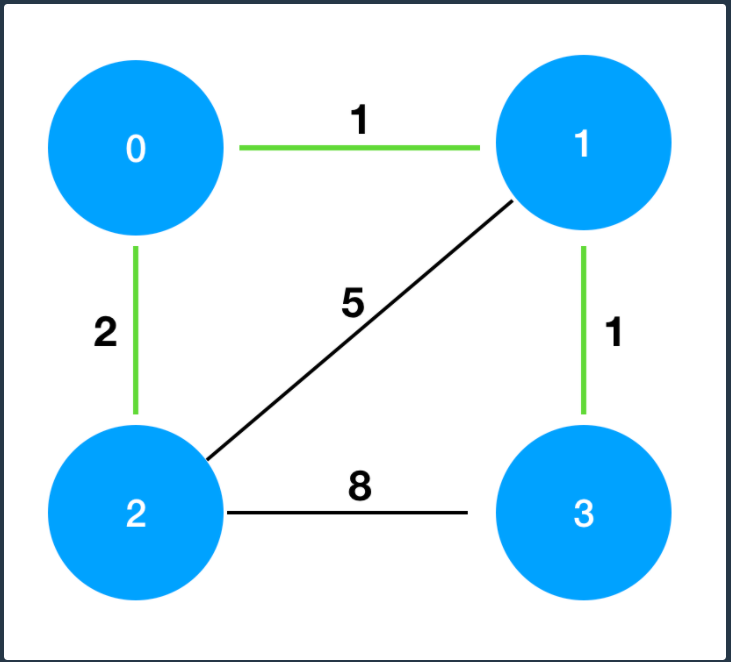
문제 풀이
import java.util.*;
class Solution {
static int[] parents;
public int solution(int n, int[][] costs) {
int answer = 0;
Arrays.sort(costs, (a, b) -> a[2] - b[2]);
parents = new int[n];
for(int i = 0; i < parents.length; i++)
parents[i] = i;
for(int[] set : costs) {
int from = set[0];
int to = set[1];
int weight = set[2];
if(unionFind(from) == unionFind(to)) continue;
answer += weight;
parents[unionFind(to)] = unionFind(from);
}
return answer;
}
public static int unionFind(int node) {
if(parents[node] == node)
return parents[node];
return unionFind(parents[node]);
}
}MST(minimum spaning tree)를 구하면 되는 문제이다. MST를 구하기 위해서는 Kruscal's Algorithm을 알아야 하고 그 안에서 unionFind라는 그래프 알고리즘에 대해서 알아야 한다.
MST - 최소 신장 트리란 뜻으로, 모든 정점들이 최소로 연결된 사이클을 포함하지 않는 spanning tree에서 연결된 간선에 가중치가 있을경우 가중치의 비용이 최소인 트리이다. 여기서 모든 정점이 최소로 연결된 사이클이 포함하지않는 spanning tree의 간선의 수는 정점을 n이라고 표현 했을때 언제나 n-1이다.
참고 자료: https://gmlwjd9405.github.io/2018/08/28/algorithm-mst.html
Union-Find - 여러개의 노드가 존재할 경우 두개의 노드를 선택하여, 현재 이 두 노드가 서로 같은 그래프에 속하는지 판별하는 알고리즘이다.
참고 자료: https://m.blog.naver.com/ndb796/221230967614
kruscal's algorithm - 가장 적은 비용으로 모든 노드를 연결하기 위한 알고리즘으로, 최소 신장 트리(MST)를 만들기 위한 대표적인 알고리즘이다.
참고 자료: https://m.blog.naver.com/ndb796/221230994142
풀이 방법
-
(출발 정점, 도착 정점, 비용)으로 이루어진 배열의 셋을 비용 기준 오름차순으로 정렬한다.
(비용이 가장 낮은 간선 부터 붙이기 시작하기 위해서) -
정점의 수 길이만큼의 배열을 만든 후 인덱스로 초기화 한다.
(모두 자기 자신으로 루트 노드를 설정하기위해) -
costs 배열을 돌면서 연결하고 이때 UnionFind 알고리즘으로 MST를 만든다.
ex) [1,2,1]일때 -> 노드 1에서 노드 2로 연결 되기 때문에 노드 1과 노드 2의 root를 확인 후 다르다면 노드 2의 root를 노드 1의 root로 업데이트한다. 만일 root가 같다면 같은 그래프에 속해 있기 때문에 연결시 cycle이 되므로 스킵한다.
