좋은 알고리즘을 선택하는데 있어서 여러 평가 기준이 있다. 그 중에 하나인 시간 복잡도에 대해 얘기하려고 한다.
먼저 알고리즘이란?
- 알고리즘이란 어떤 목적을 달성하거나 결과물을 만들어내기 위해 거쳐야 하는 일련의 과정을 의미한다.
- 알고리즘은 각기 다른 모양과 형태를 지니고 있기 때문에, 시간 복잡도를 설명하는데 자주 사용된다.
- 시간 복잡도를 분석하는 것은 input n에 대하여 알고리즘이 문제를 해결하는 데에 얼마나 오랜 시간이 걸리는 지를 분석하는 것과 같다.
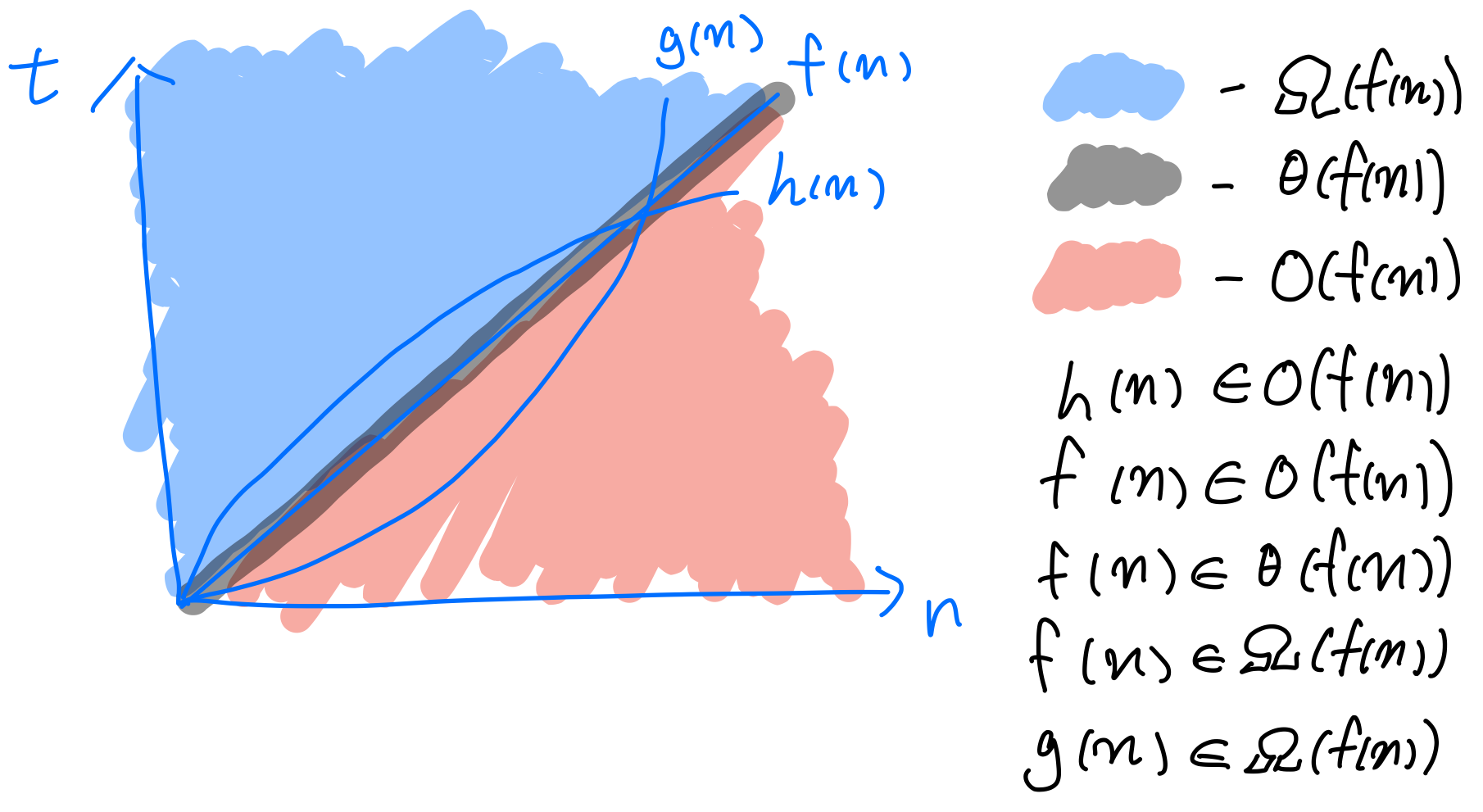
- 이를 표기하는 데에는 Big-O 표기법, Big-θ(theta) 표기법, Big-Ω(Omega) 표기법이 있다.
표기법
Big-O 표기법
-
입력 n을 받는 함수 f(n)이 있을 떄, n의 값 증가율보다 같거나 느리게 증가하는 함수의 집합을 O(f(n))이라고 한다.
-
위와 같이 어떤 알고리즘의 최악의 경우(worst case)가 f(n)일 때, 이 알고리즘의 시간이 얼마나 걸리느냐를 나타낼 때, 아무리 오래 걸려도 f(n)이 걸리므로 O(f(n))이라고 할 수 있다.
-
"f(n)의 big-oh"나 "f(n)의 O"라고 한다.
-
시간복잡도를 나타낼 때 가장 많이 쓰인다.
-
n의 값이 무한히 커졌을 때는 낮은 차항의 값은 큰 의미가 없으므로 최고차항만 신경쓰면 된다.
-
쉽게 구하는 법은 최고 차항의 계수를 땐 값을 구하면 된다.
-
Examples
- f(n) = 2 → O(1)
- f(n) = 3n + 14 → O(n)
- f(n) = 2n^2 - 3n + 123 → O(n^2)
-
O(1) - constant time (상수 시간)
-
값을 접근할 떄, 키를 알거나 인덱스를 알고 있으면 추가적인 시간 필요 없이 한 단계만 걸린다.
arr = [1, 2, 3, 4, 5] print(arr[2]) # 3
-
-
O(logN) - logarithmic time (로그 시간)
-
배열에서 값을 찾을 때, 어느 쪽에서 시작할지를 알고 시작하면 검색 시간이 줄어든다.
int bin_search(int list[], int search_value, int left, int right) { int middle; while (left <= right) { middle = (left + right) / 2; if (list[middle] < search_value) left = middle + 1; else if (list[middle] == search_value) return middle; else right = middle - 1; } return -1; }
-
-
O(n) - linear time(선형 시간)
-
순차적인 접근을 할 떄 사용된다.
int i = 0; int list[5] = {0, 1, 2, 3, 4}; while (i != 4) i++; printf("%d", i);
-
-
O(2^n) - exponential time (지수 시간)
- 지수 시간은 보통 문제를 풀기 위해 모든 조합과 방법을 시도할 떄 사용 된다.
-
속도는 1에 가까울 수록 빠르다
- O(1) : 상수형
- O(logN) : 로그형
- O(n) : 선형
- O(nlogN) : 선형로그형
- O(n^2) : 2차형
- O(n^3) : 3차형
- O(2^n) : 지수형
- O(n!) : 팩토리얼형
BIg-θ 표기법
- 입력 n을 받는 함수 f(n)이 있을 떄, n의 값 증가율과 같게 증가하는 함수의 집합을 θ(f(n))이라고 한다.
- "f(n)의 big-thetha"나 "f(n)의 theta"라고 한다.
- 구하는 법은 Big-O와 같다.
Big-Ω 표기법
- 입력 n을 받는 함수 f(n)이 있을 떄, n의 값 증가율에 비해 같거나 빠르게 증가하는 함수의 집합을 Ω(f(n))이라고 한다.
- "f(n)의 big-omega"나 "f(n)의 omega"라고 한다.
- 구하는 법은 Big-O와 같다.
