최소신장트리

신장 트리 (Spanning Tree)

• 조건 : 그래프 G는 connected graph이다.
• 정의 : 그래프 G의 spanning tree는 다음 성질을 만족하는 G의 부분 그래프이다.
  1. G의 모든 정점들이 포함되어야 한다.
  2. connected 그래프이어야 한다.
  3. 사이클을 포함하지 않아야 한다.
• 신장트리는 다음 두 가지 방식으로도 구할 수 있다.
  • DFS : DFS를 돌린 후 각 노드 v마다 (pred[v], v) 간선을 선택한다.
  • BFS : BFS를 돌린 후 각 노드 v마다 (pred[v], v) 간선을 선택한다.
• 그래프 G의 신장트리 G'는
  • V(G') = V(G)이고
  • G'는 연결 되어있는
  • 최소 부분 그래프(Minimal Subgraph)이다.
• 정점수 n인 그래프의 신장 트리는 n - 1개의 간선 가짐

최소비용 신장트리(Minimal-cost Spanning Tree)

• 최저 비용을 갖는 신장 트리
• Kruskal, Prim, Sollin 알고리즘
• 탐욕 알고리즘 (greedy method)
  • 최적해를 단계별로 구한다
  • 각 단계에서는 몇 개의 판단 기준에 따라 최상의 결정을 내린다
  • 한 번 내려진 결정은 뒤에 번복이 불가능하므로 각각의 결정이 가능한 해를 도출해낼 수 있는지 확인
• 신장트리를 만드는 제한 조건
  • 그래프 내에 있는 간선들만을 사용
  • 정확하게 n - 1개의 간선만을 사용
  • 사이클을 생성하는 간선을 사용 금지

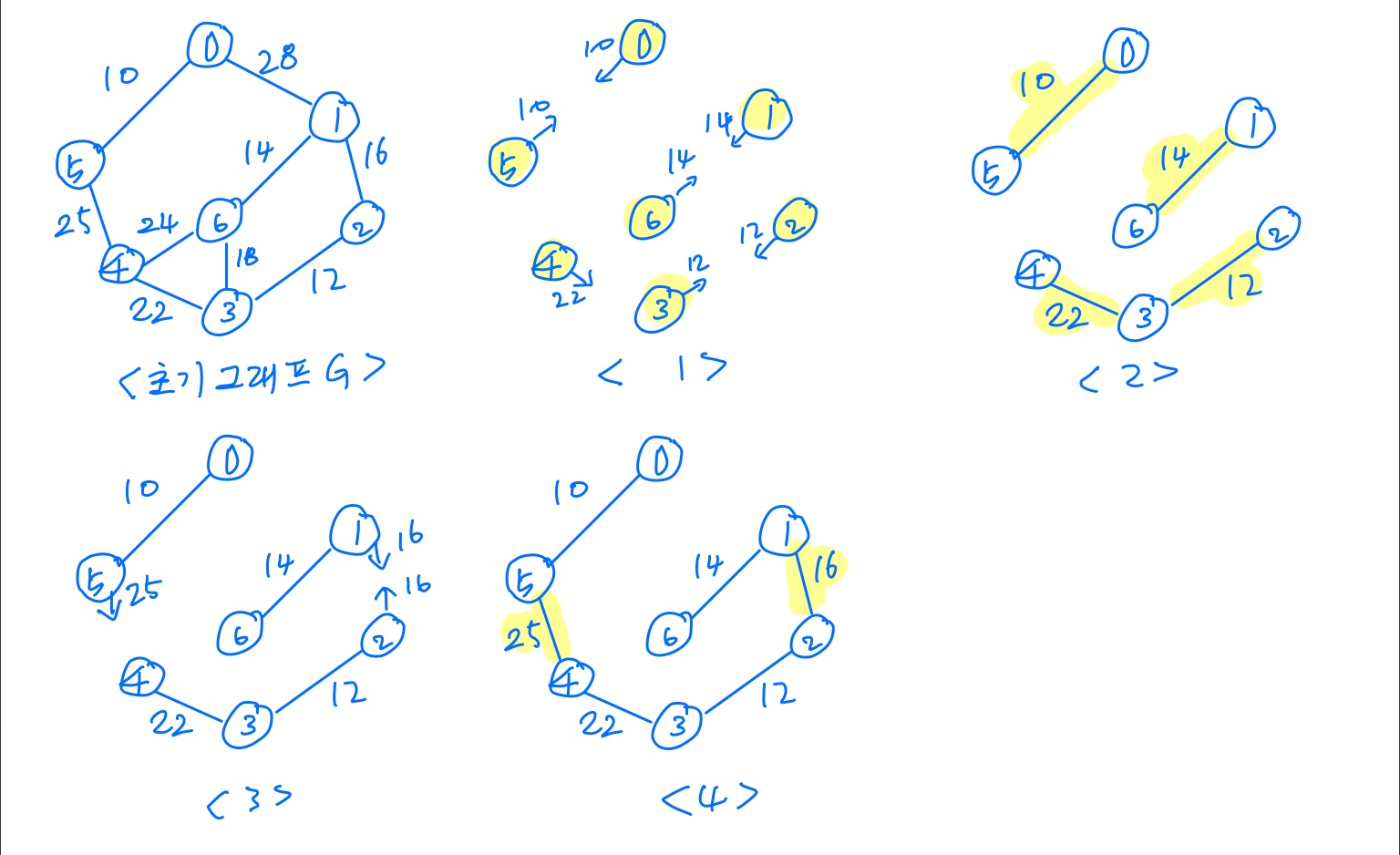
Kruskal 알고리즘

• 알고리즘

  1. 먼저 초기에 G로부터 부분그래프 T를 생성한다.
     • 처음에 T는 정점들만 가진 부분 그래프에서 시작한다.
  2. 다음과 같이 한 번에 하나씩 T에 간선을 추가해 간다.
     • 단, 추가할 경우 T에 사이클이 나타나지 않게 하는 간선을 선택해야 함
     • 종료 조건 : 총 선택된 간선의 수 = n - 1이면 종료함
     • T는 n개의 정점을 가지며 사이클 없이 n - 1개의 간선만이 T에 포함됨

• 매 단계에서 T는 여러 개의 트리를 가짐 (통틀어서 Forest라고 부른다)

• 과정 예시

  

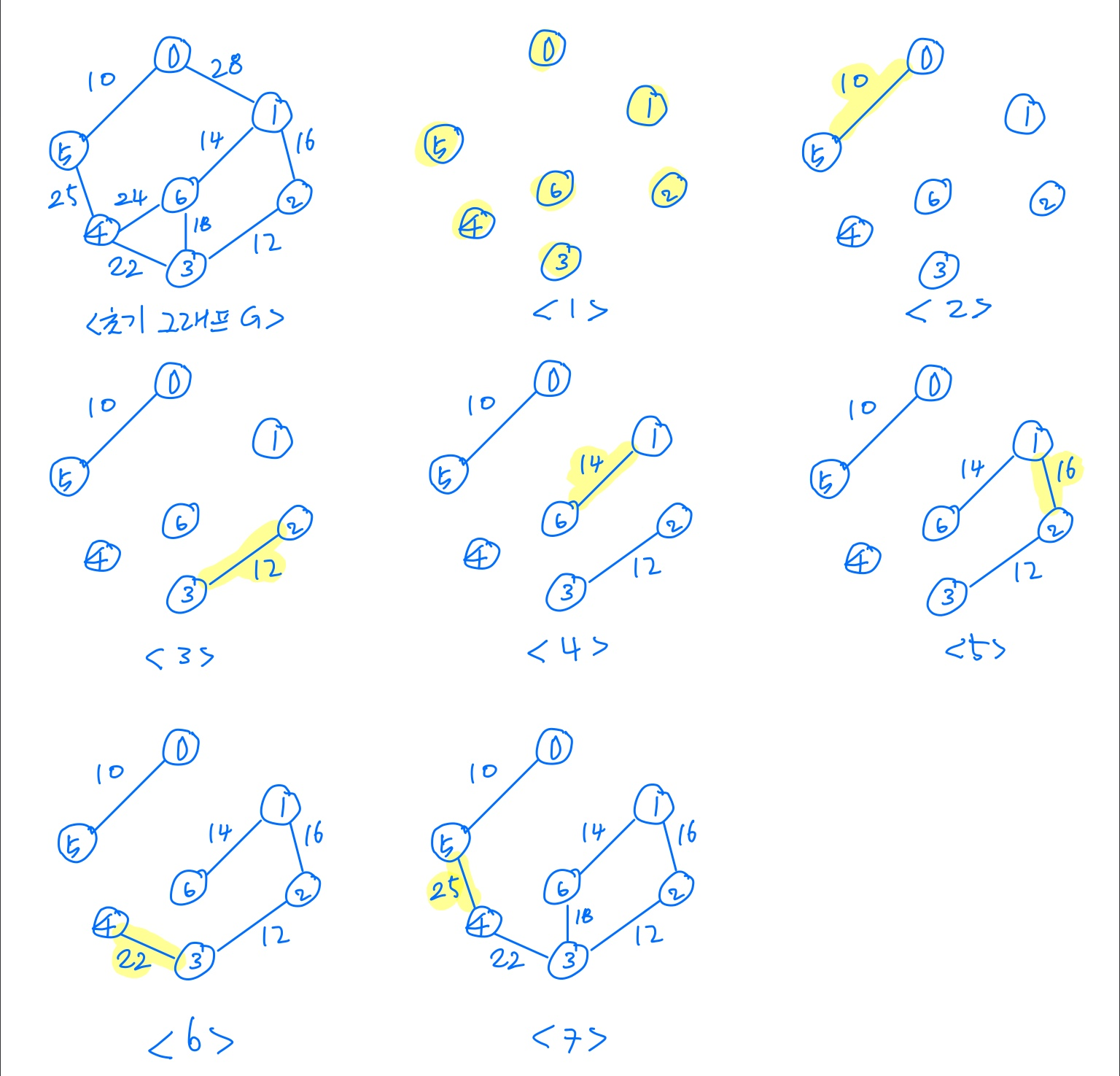
Prim 알고리즘

• Kruskal 방식과 달리 매 단계에서 T는 하나의 트리임

• 방법

  1. 하나의 정점으로 된 트리 T에서 시작
  2. T에는 없는 간선 중 한 정점이 T에 속하는 간선 하나를 선택
     • 이러한 간선을 찾을 수 없으면 알고리즘을 종료함 (실패로 종료)
     • 그런 것들 중에서 최소의 비용의 것을 선택
       -> 이 경우 사이클을 일으키지 않음. 한 노드가 T에 없으므로
     • 이 간선을 T에 추가함
       -> 이 결과로 커진 T는 트리 하나로 구성됨
  3. T에 n - 1개의 간선이 포함되어 있으면 성공으로 종료. 그렇지 않으면 다시 위의 작업을 반복

• 과정 예시

  

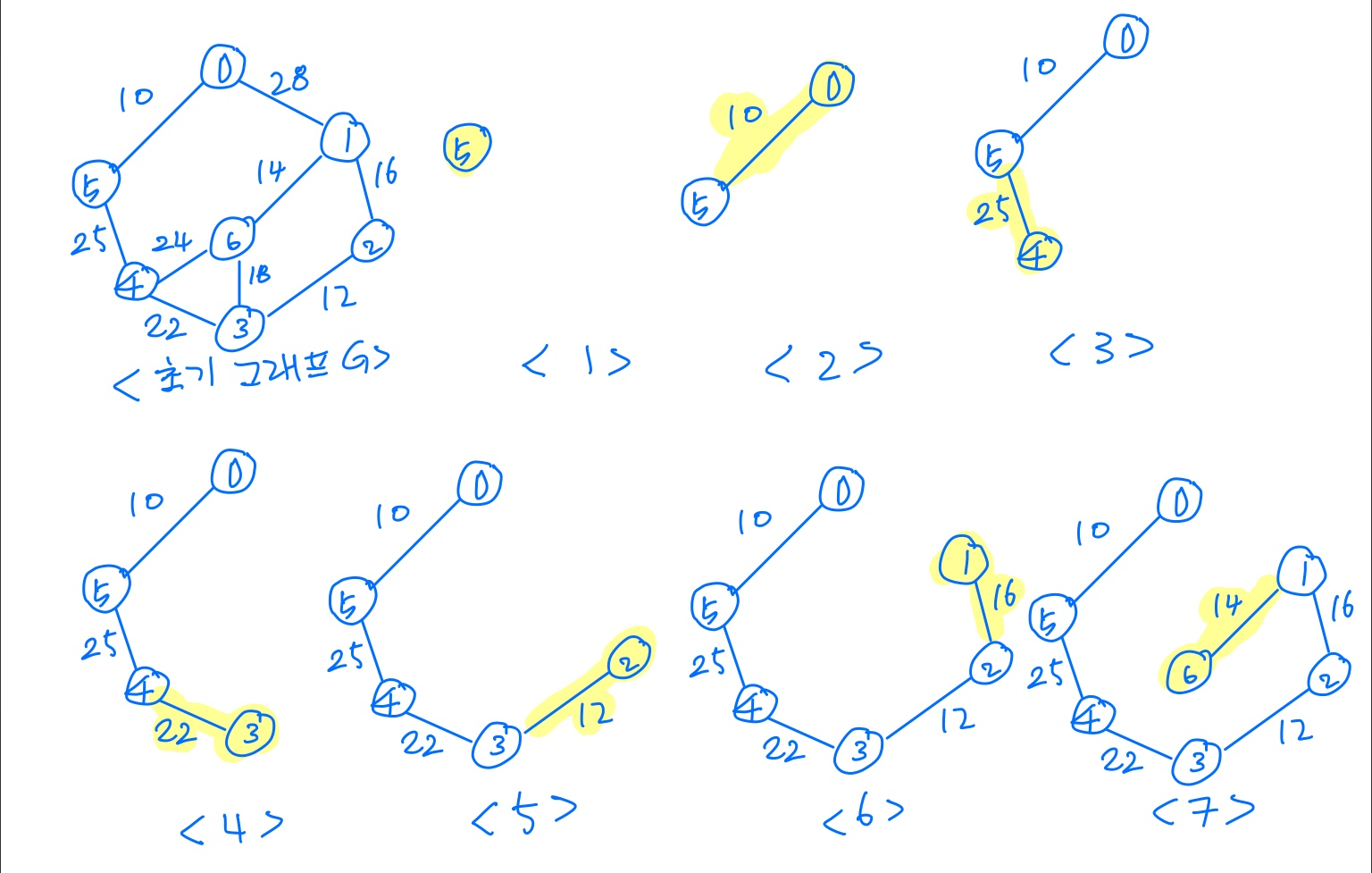
Sollin 알고리즘

• 알고리즘

  1. 각 단계에서 여러 개의 간선을 선택
  2. 각 단계에서는 포레스트에 있는 각 트리에 대해 하나의 간선을 선택
     • 이 간선은 오직 하나의 정점만 그 트리에 속한 최소 비용의 간선
  3. 선택된 간선을 구축중인 신장 트리에 추가
  4. 오직 하나의 트리만이 존재하거나 더 이상 선택할 간선이 없으면 종료

• 과정 예시