✏️ 2025. 01. 07 TIL

▶ 통계학 라이브세션 : 1회차

1. 통계학 수식

• $X$ : 확률 변수
• $x$ : 확률 변수의 실제 값
• $\sum$ : 데이터의 합
• $\mu$ : 모집단의 평균

2. 자료형의 종류

• 범주형 자료
  • 명목형 자료 : 순서가 의미없는 자료
  • 순서형 자료 : 순서가 의미있는 자료

• 수치형 자료
  • 이산형 자료: 두 데이터 구간이 유한한 자료
  • 연속형 자료: 두 데이터 구간이 무한한 자료

3. 중심 경향치

• 범주형 요약 : 최빈값(Mode) 사용
• 수치형 요약 : 평균(Mean), 중앙값(Median) 사용

4. 산포도: 데이터의 퍼짐 정도를 나타내는 방법

• IQR (Inter Quantile Range): 백분위 기준 75%(Q3)와 백분위 기준 25%(Q1)의 차이

• 분산 : 평균 기준으로 데이터가 퍼진 정도
  $Var = \sigma^2 = \frac{1}{n} \displaystyle\sum_{i=1}^{n}{(x_i-\mu)}^2$

• 표준 편차: 분산의 제곱근
  $\sigma = \sqrt{Var}$

• 변동계수: 값 스케일에 따라 분산이 달라지는 것을 보정하기 위한 방법
  $CV=\frac{표준편차}{평균}$

5. Numpy 자주 쓰는 함수

• 기본 통계 함수

  • mean() : 데이터의 평균값 계산
  • median() : 데이터의 중앙값 계산
  • std() : 데이터의 표준편차 계산
  • var() : 데이터의 분산 계산
  • sum() : 데이터의 합계 계산
  • prod() : 데이터의 곱 계산

• 퍼센타일 및 백분위 함수

  • percentile() : 데이터의 특정 퍼센타일 값 계산
  • quantile() : 데이터의 특정 분위 값 계산

• 최소값 / 최대값 관련 함수

  • min() : 데이터의 최소값 반환
  • max() : 데이터의 최대값 반환
  • argmin() : 최소값의 인덱스 반환
  • argmax() : 최대값의 인덱스 반환

• 데이터 생성 및 처리 함수

  • histogram() : 데이터에서 히스토그램 계산
  • unique() : 데이터에서 고유값 반환
  • bincount() : 정수 배열의 값의 빈도 계산

• 랜덤 데이터 생성

  • np.random.seed()
    • 난수 생성의 초기값 설정으로 재현 가능성 보장
    • 예시: np.seed(42)
  • np.random.rand()
    • 0~1 사이 균등분포에서 난수 생성
    • 예시: np.random.rand(3,2)
  • np.random.randn()
    • 표준정규분포에서 난수 생성
    • 예시: np.random.randn(4)
  • np.random.randint()
    • 정수 난수 생성
    • 예시: np.random.randint(1,10,size=5)
  • np.random.uniform()
    • 균등 분포에서 난수 생성
    • 예시: np.random.uniform(0,10, size=5)
  • np.random.normal()
    • 정해진 평균과 표준편차에서 난수 생성
    • 예시: np.random.normal(0,1,size=10
  • np.random.choice()
    • 주어진 배열에서 임의의 값을 샘플링
    • 예시: np.random.choice([1,2,3], sice=2, replace=False)

---

▶ 통계학 라이브세션 : 2회차

■ 추가 참고 자료 - https://wikidocs.net/198620

1. 모집단과 표본집단

• 모집단(Population)
  • 표본의 전체가 되는 집단 (궁극적으로 관심있는 집단)
  • 모수(Parameter) : 모집단의 특징
• 표본집단(Sample)
  • 모집단에서 특정한 방법(sampling method)를 이용하여 뽑아낸 임의의 집단
  • 특징들을 통계량(Statistic)이라고 함

2. 샘플링 편향

• 모집단의 특정 개인이나 그룹이 다른 개인이나 그룹보다 표본에 포함될 가능성이 높아 표본이 편향되거나 대표성을 갖지 못하는 상황

3. 기술통계 vs 추론통계

• 기술통계: 데이터의 특징을 이리저리 살펴보는 과정
• 추론통계: 표본으로부터 모집단을 추정(Estimation)하는 과정

4. 분포(Distribution)

• 데이터가 특정 값 중심으로 흩어진 형태를 나타내는 통계적 개념
• 이산형 vs 연속형
  • 이산형 - 데이터 사이에 끊어짐이 있는 경우. 즉, 소수점 형태로 표현되지 못하는 데이터.
  • 연속형 - 데이터와 데이터 사이에 끊어짐이 없이 연속적으로 이어진 경우. 즉, 소수점 형태로 표현할 수 있는 데이터
• 이산 확률 분포 vs 연속 확률 분포
  • 이산확률분포 - 확률질량함수(PMF)를 사용하여 각 값에 대한 확률 나타냄
  • 연속확률분포 - 확률밀도함수(PDF)를 사용하여 특정 구간에 대한 확률 계산
• 장점
  • 데이터의 요약(중앙값, 평균, 분산) 등에 대한 수식 표현 가능
  • 모집단을 추정하는 가설의 기반

5. 베르누이 분포 (Bernoulli Distribution)

• 확률 변수가 취할 수 있는 경우가 2가지인 경우 (예 - 동전 던지기, 클릭 등)

• 확률 질량 함수: 특정 값이 발생할 확률을 나타내는 함수

• 베르누이 확률 질량 함수 수식

  $P(X=x) = p^x(1-p)^{1-x},$ $x \in \{{0,1\}}$

  • $P$ : 확률
  • $X$ : 확률 변수
    → $X=1$은 성공, $X=0$은 실패를 나타냄
  • $x$ : 확률 변수의 실제 값
  • $p$ : 확률 실제값

6. 이항 분포(Bionomial Distribution)

• 베르누이 시행을 독립적으로 반복하여 결과를 관찰하는 경우 사용
• 이진(binary) 결과를 가지는 시행에서 성공 횟수의 확률분포를 나타내는데 사용

• 이항 분포의 조건
  • 각 시행은 두 가지 가능한 결과 중 하나인 '성공'과 '실패'로 나뉨
  • 각 시행은 독립적. 이전 시행의 결과는 현재 시행에 영향을 주지 않음.
  • 각 시행에서의 성공 확률은 고정. 동일한 성공 확률로 시행이 반복됨.

• 이항 분포 표현식
  $B(n,p)$
  • $n$ : 시행횟수
  • $p$ : 성공확률

• 이항 분포의 확률 질량 함수 수식

  $P=(X=k) = {n}C_{k}p^k(1-p)^{n-k}$

  • $P=(X=k)$ : 확률 변수 $X$가 $k$라는 값을 가질 확률
  • $n$ : 독립 시행의 총 횟수
  • $k$ : 성공한 횟수 (예: 동전을 10번 던져 3번 앞면이 나온다면 $k=3$
  • ${n}C_{k}$ : 조합, 즉, $n$번 시행 중에서 $k$번 성공하는 경우의 수
    • 계산식
      $nC_k = \binom{n}{k} = \frac{n!}{k!(n-k)!}$
  • $p$ : 성공 확률 (각각의 시행에서 성공할 확률)
    • 예를 들어, 동전을 던질 때 앞면이 나올 확률은 $p=0.5$
  • $p^k$: 성공 확률 $p$가 $k$번 발생할 확률
    • 예: $p=0.5$, $k=3$이라면 $p^k = (0.5)^3 =0.125$
  • $(1-p)$ : 실패 확률 (각각의 시행에서 실패할 확률)
    • 예: 성공 확률이 $p=0.3$이라면 실패 확률은 $1-p=0.7$
  • $(1-p)^{n-k}$
    • 실패 확률 $(1-p)$가 $n-k$번 발생할 확률을 나타냄
    • 예: $n=5$, $k=2$, $1-p=0.7$이라면 $(1-p)^{n-k}=(0.7)^{5-2}=(0.7)^3=0.343$

• 이항 분포의 정규 근사

  $B(n, p) \approx N\left(np, \sqrt{np(1-p)}\right)$

  • 좌변 : $B(n, p)$

    • 이항 분포 : $n$번의 독립적인 시행에서 성공 확률이 $p$인 분포

  • 우변 : $N(\mu, \sigma^2)$

    • 정규 분포로 근사된 표현
      • $\mu = np$ : 평균적으로 성공할 횟수
      • $\sigma = \sqrt{np(1-p)}$: 이항 분포의 표준편차

  • 정규 근사 조건

    • $n$이 충분히 크고 $p$가 0이나 1에 너무 치우치지 않은 경우, 해당 데이터를 정규분포로 간주할 수 있음
    • $n\cdot p\geq5$
    • $n\cdot (1-p) \geq5$

7. 균등 분포(Uniform Distribution)

• 모든 값이나 구간이 동일한 확률을 가지는 분포
  • 이산 균등 분포: 특정한 정수 값들이 동일한 확률을 가짐
  • 연속 균등 분포: 특정 구간 내에서 모든 값이 동일한 확률 밀도를 가짐

8. 정규분포(Normal Distribution)

• 평균을 기준으로 좌우대칭
• 종모양으로 봉우리가 1개인 연속 확률 분포
• 자연 현상의 경우, 대부분 이 분포를 따름
  
  

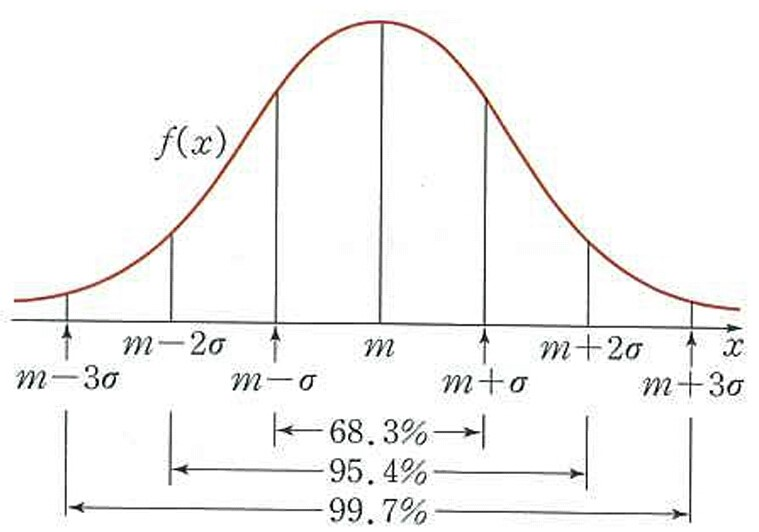
• 정규 분포의 장점

  • 평균과 표준편차를 알고 있으면 전체 데이터의 몇 %에 포함되는지 알 수 있음

• 정규 분포 표현식

  $N\sim(\mu, \sigma^2)$

  • 확률 변수 $N$이 평균 $\mu$, 분산 $\sigma^2$를 가지는 정규분포를 따른다는 의미

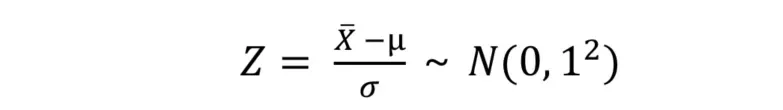
9. 왜도와 첨도

• 왜도(skewness): 확률의 비대칭 정도를 나타내는 측도
  • 긴꼬리 분포라고도 하며 보통 결제 금액, 월급과 같은 수치가 right skewness 특성을 띈다.
• 첨도(kurtosis) : 종모양의 뾰족한 정도를 나타내는 측도
  • 첨도가 정규분포보다 낮으면 뭉툭한 모양으로 이상치가 적음
  • 첨도가 정규분포보다 높으면 꼬리(tail)가 길고 이상치가 많음

10. 표준정규분포

• $\mu = 0,\sigma = 1$인 정규 분포
  ( 평균이 0이고 표준편차가 1인 정규 분포)
• 달성하기 위하여 모든 데이터에 대해 '정규화' 수행
  • 정규화(Nomalization) : 어떤 대상을 규칙이나 기준에 따른 상태로 만드는 방법
  • 추론 통계에서는 '모든 데이터에서 평균을 빼고 표준편차를 나누는 방법'을 말함
  • 또한 모든 Z값에 대해서 계산해 놓은 표가 있는데 이를 표준정규분포표라고 함
  • 아래의 표는 Z값의 왼쪽 끝부터 해당하는 X값 까지 누적된 확률값을 제공
    

11. Scipy 모듈

• 공학, 사회과학 등에 자주 사용하는 기초통계 모듈과 함수를 모아놓은 라이브러리

• Scipy 자주 쓰는 라이브러리

  • stats : 통계 분석과 확률 분포 관련 함수 제공
  • norm : 정규 분포 관련 함수 (PDF, CDF, 랜덤 샘플링 등)
  • uniform : 균등 분포
  • bernoulli : 베르누이 분포
  • binom : 이항분포
  • ttest_ind : 독립 두 표본에 대한 t-검정
  • ttest_rel : 대응표본 t-검정
  • mannwhiteneyu : Mann-Whitney U 비모수 검정
  • chi2_contingency : 카이제곱 독립성 검정
  • shapiro : Shapiro-Wilk 정규성 검정
  • kstest : Kolmogorov-Smirnov 검정 (분포 적합성 검정)
  • probplot : Q-Q plot 생성 (정규성 시각화)
  • pearsonr : Pearson 상관계수 계산
  • spearmanr : Spearman 순위 상관계수 계산
  • describe : 기술 통계량 제공 (평균, 표준편차 등)

• scipy.stats 메소드
  ▶ scipy.stats 메뉴얼

  • rvs : 난수 생성

    • Numpy의 Random 모듈에 대응
    • scipy.stats.norm.rvs(loc= 1150, scale = 150, size = 1, random_state= None)
    • loc : 평균
    • scale : 표준편차
    • size : 생성할 데이터 갯수
    • random_state : 시드 설정

  • pdf : 특정 위치의 확률 구하기

    • pdf ⇒ Probability density function(확률밀도함수)
    • scipy.stats.norm.pdf(x = 1380, loc = 1150, scale = 150)
    • x : 구할 x축 값
    • loc : 평균
    • scale : 표준편차

  • cdf : 누적확률 분포 구하기

    • cdf ⇒ cumulative density function(누적밀도함수, pdf의 적분값)
    • pdf와 전달인자는 같으나 누적된 확률(밑변 넓이)를 구함
    • scipy.stats.norm.cdf(x = 1380, loc = 1150, scale = 150)
    • x : 구할 x축 값
    • loc : 평균
    • scale : 표준편차

  • ppf : 백분율을 알때 거꾸로 x 값 구하기

    • ppf: percent point function
    • cdf의 역함수
    • scipy.stats.norm.ppf(q = 0.937, loc = 1150, scale = 150)
      • q : 백분율
      • loc : 평균
      • scale : 표준편차

---

▶ 통계학 기초 1주차

1. 기술 통계

• 데이터를 요약하고 설명하는 통계 방법
  • 주로 평균, 중앙값, 분산, 표준편차 등을 사용 → 데이터를 특정 대표 값으로 요약

2. 추론 통계

• 표본 데이터를 통해 모집단의 특성을 추정하고 가설을 검정하는 통계 방법
  • 주로 신뢰구간, 가설검정 등을 사용

• 신뢰 구간 (Confidence Interval)
  • 모집단의 평균이 특정 범위 내에 있을 것이라는 확률을 나타냄
  • 일반적으로 95%의 신뢰 구간 사용

• 가설 검정 (Hypothesis Testing)
  • 가설검정은 모집단에 대한 가설을 검증하기 위해 사용
  • 귀무가설(H0) : 검증하고자 하는 가설이 틀렸음을 나타내는 기본 가설
  • 대립가설(H1) : 그 반대 가설로 주장하는 바를 나타냄
  • p-value를 통해 귀무가설을 기각할지 여부를 결정

3. 다양한 분석 방법

• 위치 추정: 데이터의 중심을 확인하는 방법
  → 대표적으로 평균, 중앙값 확인

• 변이추정: 데이터들이 서로 얼마나 다른지 확인하는 방법
  → 분산, 표준편차, 범위(range) 등을 사용

• 데이터 분포 탐색: 데이터의 값들이 어떻게 이루어져 있는지 확인
  → 히스토그램, 박스 플롯: 데이터의 분포를 시각적으로 표현하는 대표적인 방식

• 이진 데이터와 범주 데이터 탐색: 데이터들이 서로 얼마나 다른지 확인
  → 최빈값(개수가 가장 많은 값)을 주로 사용
  → 파이 차트, 바 그래프: 이진 데이터와 범주 데이터의 분포를 표현하는 대표적인 방법

• 상관관계: 데이터끼리 서로 관련이 있는지 확인하는 방법
  → 상관계수 : 두 변수 간의 관계 측정

• 인과관계와 상관관계의 차이

  • 상관관계: 두 변수 간의 관계를 나타냄
  • 인과관계: 한 변수가 다른 변수에 미치는 영향을 나타냄

• 두 개 이상의 변수 탐색 : 여러 데이터들끼리 서로 관련이 있는지 확인
  → 다변량 분석 : 여러 변수 간의 관계를 분석하는 방법