11장 : 기계 학습

11.1 모델링

• 개념 : 다양한 변수 간의 수학적 (혹은 확률적) 관계를 표현한 것
• 예시
  • SNS 상에서 사용자수, 사용자당 광고수익 → 차후 몇년 간의 연간 수익
  • 요리책에서 먹는 사람의 수, 배고픈 정도 → 재료의 양
  • 미국 경기지표, 미국 주식 지표 → 한국 주가 지수

11.2 기계 학습

• 정의 : 데이터를 통해 모델을 만들고 사용하는 것

• 예측 모델링, 데이터 마이닝이라고도 불린다.

• 보통 주어진 데이터로 모델을 구축하고, 새로운 데이터에 만들어진 모델을 적용하면 다음과 같이 다양한 것을 예측해볼수 있다

  • 이메일이 스팸 메일인지 아닌지 예측
  • 신용카드 사기 예측
  • 쇼핑 고객이 클릭할 확률이 높은 광고 예측
  • 슈퍼볼에서 우승할 미국 축구팀 예측

<종류>

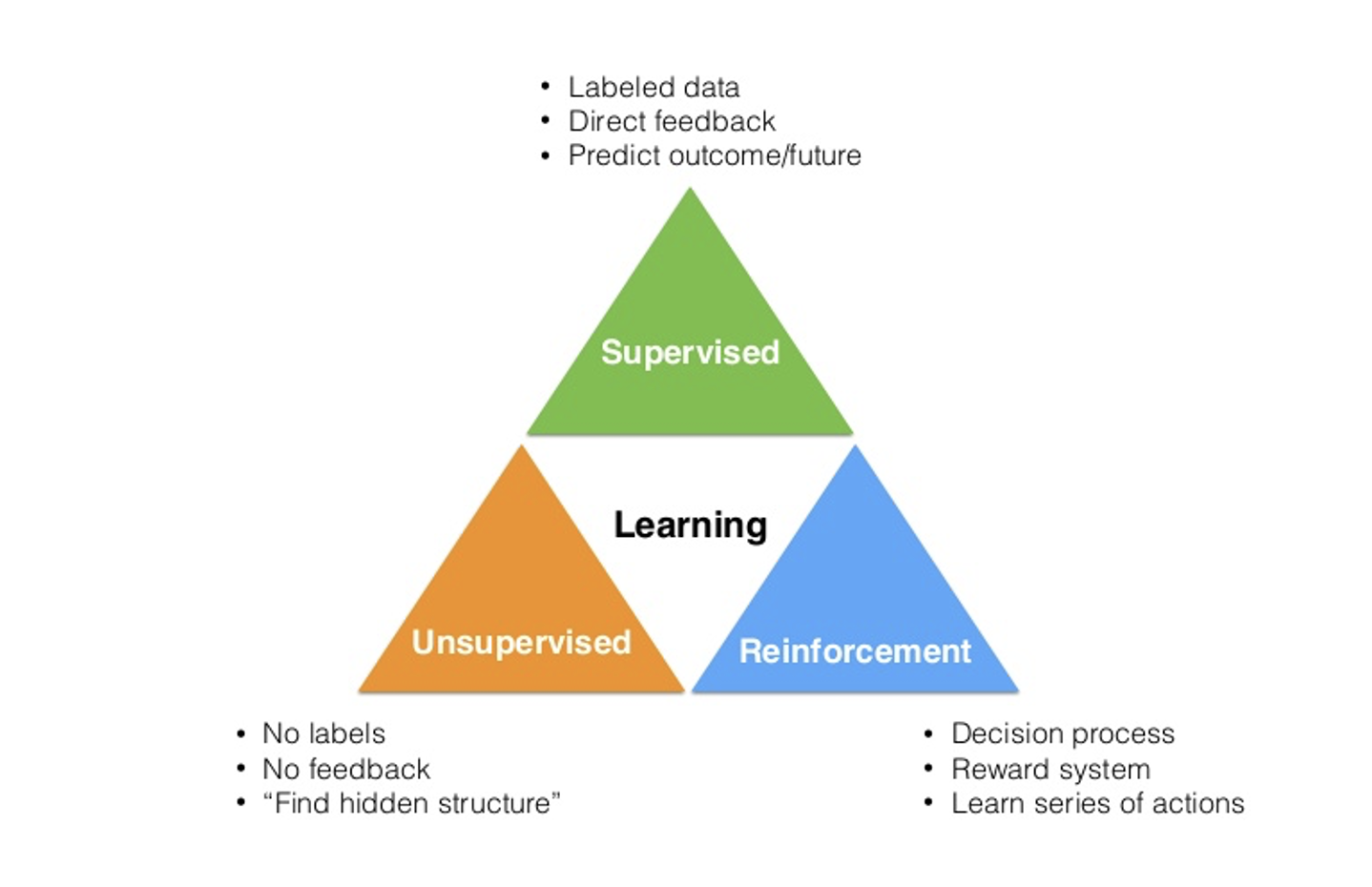
• 지도 학습 : 학습에 사용될 데이터에 답(종속 변수 값)이 포함되어있는 학습
• 비지도 학습 : 답(종속 변수값) 이 없는 데이터를 활용해 학습
• 준지도 학습 : 답(종속 변수값) 이 일부에만 있는 데이터를 활용
• 온라인 학습 : 새로 들어오는 데이터를 통해 모델을 끊임 없이 조정
• 강화 학습 : 연속된 예측 뒤 모델이 얼마나 잘 예측 했는지 파악 후 모델을 조정

11.3 Overfitting 과 Underfitting

• Overfitting (오버피팅)
  • 기계 학습의 일반적인 문제점
  • 만들어진 데이터모델이 학습데이터에서는 좋지만 새로운 데이터에서는 좋지 않은 경우
  • 원인 : 학습 데이터의 잡음이나 불필요한 데이터를 모델에 학습 반영
  • 문제점 : 새로운 데이터에 대한 예측의 부적확성
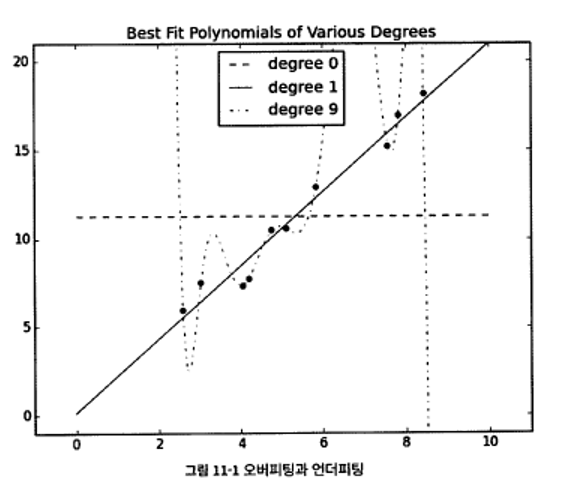
  • 예시 : 옆 그림의 9차 함수 (점선)
• Underfitting (언더피팅)
  • 만들어진 데이터 모델의 성능이 학습 데이터에서도 좋지 않은 경우
  • 원인 : 부적합한 모델 선택, 모델을 변경해야 함
  • 문제점 : 학습 데이터도 부정확한 예측
  • 예시 : 아래 그림의 상수 함수 (가로 점선)

적합 모델을 찾기 위한 실험 설계

• 적합 모델 찾기 : 학습과 평가 (테스팅) → 학습 데이터와 테스트 데이터의 분할
• 모델 실험 설계

  • hold-out 기법

    전체 데이터에서 7:3 또는 8:2 등 비율로 훈련 데이터와 테스트 데이터로 나눈다

    훈련 데이터(training set)는 모델을 개발하기 위해, 테스트 데이터(test set)는 모델을 평가하기 위해 사용
    

  • k-묶음 교차검증

    전체 데이터를 k-묶음으로 나눈 후 (k-1)개 묶음
    

  • hold-out + validation 기법

    검증 데이터 셋을 추가하여, 훈련 데이터에 다시 hold-out 기법을 적용한 방법 
    
    검증 데이터셋은 훈련 데이터로 개발된 여러 모델의 성능을 비교하는데 사용되며, 선정된 최선의 모델의 성능은 테스트 데이터셋을 이용하여 평가 

    hold-out 방식으로 데이터 분할

    import random
    from typing import TypeVar, List, Tuple
    
    X = TypeVar('X')
    
    def split_data(data: List[X], prob: float) -> Tuple[List[X], List[X]]:
        # 데이터를 섞지 않고 나누는 함수
        idx = int(len(data) * prob)  # 데이터를 나누는 인덱스 계산
        return data[:idx], data[idx:]  # 데이터를 나누어 반환
    
    data = [n for n in range(1000)]  # 0부터 999까지의 숫자로 이루어진 데이터 생성
    train, test = split_data(data, 0.75)  # 데이터를 나눔
    
    # 반환된 데이터의 길이가 올바른지 확인
    assert len(train) == 750
    assert len(test) == 250
    
    # 반환된 데이터가 원본 데이터를 포함하고 있는지 확인
    assert sorted(train + test) == data

    독립(x), 종속(y) 형태의 데이터 분할

    학습 데이터, 평가 데이터에 x와 y가 제대로 쌍을 이뤄서 들어갈수 있도록 한다.

    Y = TypeVar('Y')    # 출력 변수를 표현하기 위한 일반적인 타입 
    
    def train_test_split(xs: List[X],                     
    					ys: List[Y],                     
                        test_pct: float) -> Tuple[List[X], List[X], List[Y], List[Y]]:    
        
        # Generate the indices and split them.    
        idxs = [i for i in range(len(xs))]    
        train_idxs, test_idxs = split_data(idxs, 1 - test_pct)    
        
        return ([xs[i] for i in train_idxs],  # x_train            
                [xs[i] for i in test_idxs],   # x_test            
                [ys[i] for i in train_idxs],  # y_train            
                [ys[i] for i in test_idxs])   # y_test
    
    xs = [x for x in range(20)]    # xs are 1 ... 1000
    ys = [2 * x for x in xs]       # each y_i is twice 
    x_train, x_test, y_train, y_test = train_test_split(xs, ys, 0.25)
    
    print(xs, ys)
    print(x_train, x_test)
    print(y_train, y_test)
    
    # 비율이 맞는지 확인
    assert len(x_train) == len(y_train) == 750
    assert len(x_train) == len(y_test) == 250
    
    # 대응되는 데이터들이 잘 짝지어졌는지 확인
    assert all(y == 2 * x for x, y in zip(x_train, y_train))
    assert all(y == 2 * x for x, y in zip(x_test, y_test))
    
    # 모델 학습 하고, 성능 평가 
    model = SomeKindOfModel()
    x_train, x_test, y_train, y_test = train_test_split(xs, ys, 0.33)
    model.train(x_train, y_train)
    performance = model.test(x_test, y_test)

    sklearn.model_selection.train_test_split(*arrays, test_size=None, train_size=None, random_state=None, shuffle=True, stratify=None)

  • Split arrays or matrices into random train and test subsets

  • Param

    test_size, train_size: *float (0.0~1.) or int, default=None*
    

  • Returns

    splitting*list, length=2 * len(arrays)*
    

11.4 정확도

모델의 분류와 정답

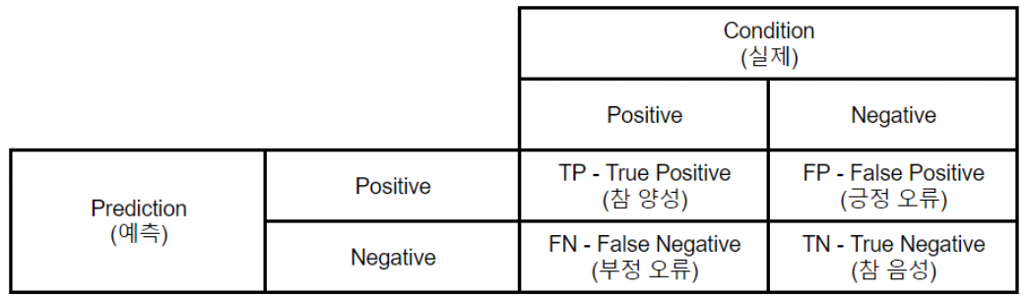
• True Positive(TP) : 실제 Positive인 정답을 Positive라고 예측 (정답)
• False Positive(FP) : 실제 Negative인 정답을 Positive라고 예측 (오답)
• False Negative(FN) : 실제 Positive인 정답을 Negative라고 예측 (오답)
• True Negative(TN) : 실제 Negative인 정답을 Negative라고 예측 (정답)

정확도 (accuracy)

• accuracy = (tp + tn) / (tp + fp + fn + tn)

• 높게 나와도 의미가 없을 수 있음

• 정밀도(Precision) : Positive 라고 분류한 것 중에서 실제 Positive 인 것의 비율

• 재현율(Recall) : 실제 Positive 인 것 중에서 모델이 Positive라고 예측한 것의 비율

• 특이도(Specificity) : 실제 Negative 중 맞춘 Negative(TN)의 비율

• 위양성율(FRP : False Positive Rate) : 실제 Negative 중 틀린 Positive(FP)의 비율

• 위음성율(FNR : False Negative Rate) : 실제 Positive 중 틀린 Negative(FN)의 비율

• 환자 적용

  • 실제 확자를 환자로 판단하는 비율 : Recall, Sensitvity, HitRate
  • 실제 환자를 비환자로 판단하는 비율 : FNR
  • 비환자(건강한 사람)을 환자로 판단하는 비율 : FPR
  • 비환자(건강한 사람)을 비환자로 판단하는 비율 : Specifity

• 정밀도와 재현율의 트레이드 오프 관계

  • 정밀도를 높이려면 가급적 FP가 작아야 한다 → 가급적 negative로 예측해야 함
  • 재현율을 높이려면 가급적 FN이 작아야한다 → 가급적 positive로 예측해야 함

• 조화 평균

  • 주어진 수들의 역수와 산술평균의 역수
  • 정밀도와 재현율의 조화 평균