📡 해싱 (hashing)
해시, 해시 테이블 , 해시 함수
데이터를 효율적으로 관리하기 위해, 임의의 길이 데이터를 고정된 길이의 데이터로 매핑하는 것을 해시라 한다
해시함수(hash function)란 데이터의 효율적 관리를 목적으로 임의의 길이의 데이터를 고정된 길이의 데이터로 매핑하는 함수입니다. 이 때 매핑 전 원래 데이터의 값을 키(key), 매핑 후 데이터의 값을 해시값(hash value)
, 매핑하는 과정 자체를 해싱(hashing)라고 한다
해싱은 key에 산술적인 연산을 적용하여 항목이 저장되어 있는 테이블의 주소를 계산하여 항목에 접근한다. 키에 대한 연산에 의해 직접 접근이 가능한 구조를 해시 테이블이라 부르며, 해시 테이블을 이용한 탐색을 해싱이라 한다.
이상적인 해싱
add(key, value) :
index <- hash_function(key)
ht[index] = value
search(key):
index <- hash_function(key)
return ht[index]하지만 하나의 키당 해시테이블에서 하나의 공간을 할당 할 수가 없다.
보통의 경우 키는 매우 많고, 해시 테이블의 크기는 상당한 제약을 받는다.
🕰️ 해시 함수
해싱에서 키 값을 해시 테이블의 주소로 변환하는 해시 함수가 잘 설계되어야만 탐색의 효율이 증대된다.
좋은 해시 함수의 조건
- 충돌이 적어야한다
- 해시함수 값이 해시테이블의 주소 영역 내에서 고르게 분포되어야 한다
- 계산이 빨라야 한다.
제산 함수
나머지 연산자 mod 를 사용하여 키를 해시 테이블의 크기로 나눈 나머지를 해시 주소로 사용하는 방법
가장 일반적인 해시 함수로 해시 테이블의 크기 M은 주로 소수(primary number)로 선택된다.
M이 짝수나 홀수라면 k가 짝수나 홀수만 될 가능성이 높고, 한쪽으로 편향된다면 해시 테이블을 골고루 사용하지 않는 것이 되서 M이 소수라면 0 ~ (M-1) 까지 골고루 사용되는 값이 나온다.
폴딩 함수
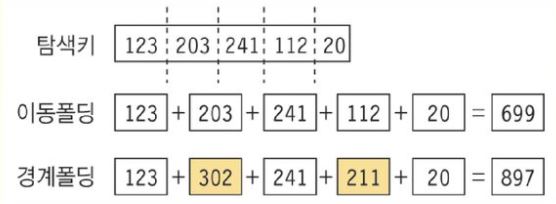
폴딩이란 탐색 키를 몇개의 부분으로 나누어 이를 더하거나 비트별로 XOR 같은 부울 연산을 하는 것을 말한다.
키를 여러부분으로 나누어 모두 더한 값을 해시 주소로 사용한다. 키를 나누고 더하는 방법에는 이동폴딩과 경계 폴딩이 대표적이다.
주로 탐색 키가 해시 테이블의 크기보다 더 큰 정수일 경우에 사용된다.
이동폴딩 : 키를 여러부분으로 나눈 값들을 더하여 해시 주소로 사용
경계폴딩 : 키의 이웃한 부분을 거꾸로 더하여 해시 주소로 사용
중간 제곱 함수
키를 제곱한 다음, 중간의 몇 비트를 취해서 해시 주소를 생성한다. 제곱한 값의 중간 비트들은 대개 키의 모든 문자와 관련이 있기 때문에 서로 다른 키는 몇개의 문자가 같을지라도 서로 다른 해싱 주소를 갖게 된다.
비교적 고르게 분산
비트 추출 방법
해시 테이블의 크기가 M = 2^k 일때 키를 이진수로 간주하여 임의의 위치 k개의 비트를 해시 주소로 사용
간단한 방법이지만, 키의 일부 정보만 사용해 해시 주소의 집중 현상이 일어날 가능성 높음
숫자 분석 방법
숫자로 구성된 키에서 각각의 위치에 있는 수의 특징을 미리 알고 있을 때 유용하다. 키의 각각의 위치에 있는 숫자 중에서 편중되지 않는 수들을 해시테이블의 크기에 적합한 만큼 조합하여 해시 주소로 사용하는 방법
🔗 참조한 사이트
⌜C언어로 쉽게 풀어쓴 자료구조⌟ 개정3판, 천인국, 생능출판
https://ratsgo.github.io/data structure&algorithm/2017/10/25/hash/
🌱 추가로 공부하면 좋은 부분
개방 주소법 - 선형조사법, 이차 조사법, 이중 해싱법, 체이닝
해싱의 성능 분석