힙(Heap)

Dayon·2023년 2월 18일

CS 자료구조

자료구조

목록 보기

4/10

🤡 힙의 개념

일반적인 배열은 크기가 고정되어있다. 이 고정된 크기로 처음에 결정된 크기 보다 더 큰 입력이 들어온다면 처리하지 못할것이고, 작은 입력이 들어온다면 남은 메모리 공간은 낭비되게 된다.

동적 메모리 할당

동적 메모리 할당(dynamic memory allocation) 은 프로그램 실행 중에 프로그램이 필요한 만큼의 메모리를 할당하는 것을 말한다. 메모리 사용량을 정확히 예측할 수 없거나 메모리 사용량이 변화하는 경우, 동적 메모리 할당은 프로그램이 필요한 시점에 필요한 만큼의 메모리를 할당할 수 있도록 해준다. 이를 통해 프로그램은 메모리 부족 없이 실행될 수 있다.

동적메모리 할당 코드

int *p;
p = (int *)malloc(sizeof(int));   // 1️⃣ 동적 메모리 할당
*p = 1000;       // 2️⃣ 동적 메모리 사용
free(p);         // 3️⃣ 동적 메모리 반납

1️⃣ 동적 메모리 할당 : malloc() 함수는 size byte 만큼 메모리 블록 할당 , 블록의 시작 주소 반환
2️⃣ 동적 메모리 사용 : 포인터 p가 가르키는 장소에 1000이 저장된다.
3️⃣ 동적 메모리 반납 : free() 함수는 할당된 메모리 블록을 운영체제에 반환. 이때 malloc()의 반환값한 포인터 값을 잊어버리면 동적 메모리 반환을 할 수 없다.

우선 순위 큐

우선순위 개념을 큐에 도입한 자료구조

보통의 큐는 선입선출(FIFO)의 원칙에 의해 먼저 들어온 데이터가 먼저 나가게 된다. 하지만 우선순위 큐(priority queue)에서는 데이터들이 우선 순위를 가지고 있고, 우선순위가 높은 데이터가 먼저 나가게 된다.

우선순위 큐는 배열, 연결리스트 등의 여러가지 방법으로 구현이 가능한데, 가장 효율적인 구조가 heap 이다.

우선순위 큐의 구현 방법

정렬이 되어 있지 않은 배열 = 배열의 맨 끝에 새로운 요소 추가 (삽입 : 시간복잡도 $O(1)$ )
정렬이 되어 있는 배열 = 새로운 요소 삽입시 다른 요소 와 값을 비교해 삽입 위치 결정 (순차 탐색, 이진탐색등 방법 이용, 삽입 : 시간복잡도 $O(n)$ )

자료구조 → 완전 이진 트리의 일종 , 힙

힙

힙(heap)은 동적 메모리가 할당되는 공간이다. 힙은 프로그램의 동적 메모리 사용을 효율적으로 관리하여 메모리 부족 오류를 방지하고 메모리 낭비를 줄인다.

힙은 여러개의 값들 중에서 가장 큰 값이나 가장 작은 값을 빠르게 찾아내도록 만들어진 자료구조
부모노드의 키 값이 자식 노드의 키 값보다 항상 큰 이진 트리 함수
중복된 값 허용함 , 이진 탐색 트리는 중복 된 값을 허용하지 않는다. (느슨한 정렬상태)

힙 종류

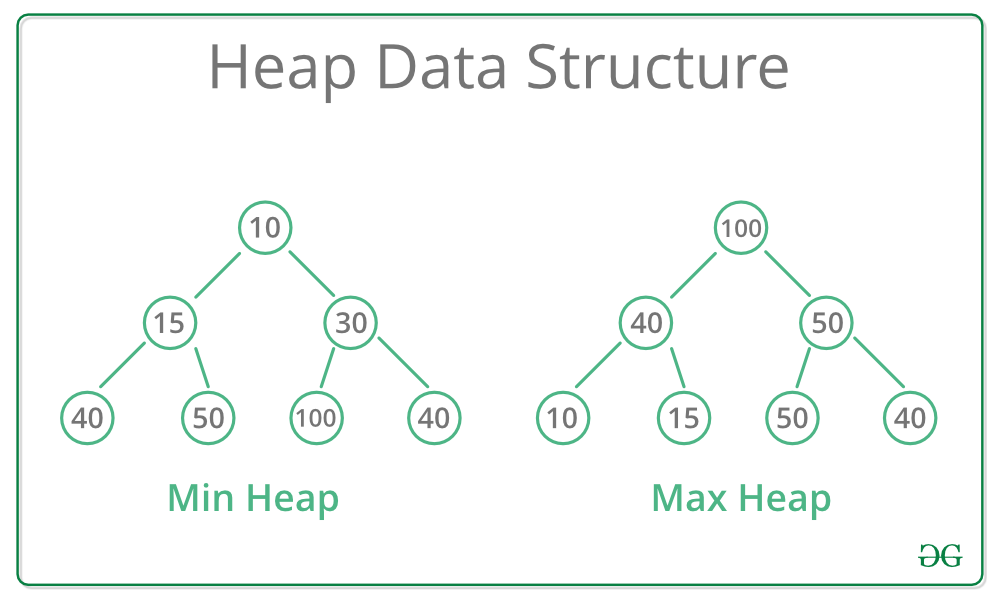
최대 힙 (Max Heap) : 부모 노드의 키 값이 자신 노드의 키값보다 크거나 같은 완전 이진 트리

$key(부모노드) ≥ key(자식 노드)$

최소 힙 (Min Heap) : 부모 노드의 키값이 자식 노드의 키값보다 작거나 같은 완전 이진 트리

$key(부모노드) ≤ key(자식 노드)$

🕰️ 힙의 구현

힙은 완전 이진 트리이기 때문에 각가의 노드에 차례대로 번호를 붙일 수 있고, 이 번호를 배열의 인덱스로 생각하면 배열에 히프의 노드들을 저장할 수 있다.

프로그램의 구현을 쉽게 하기 위해 배열의 첫번째 인덱스인 0은 사용되지 않는다.

특정 위치의 노드 번호는 새로 노드가 추가되어도 변하지 않는다.

어떤 노드의 왼쪽이나 오른쪽 자식의 인덱스를 알고 싶으면 다음 식을 이용할 수 있다.

왼쪽 자식의 인덱스 = (부모의 인덱스) * 2

오른쪽 자식의 인덱스 = (부모의 인덱스) * 2 + 1

반대로 부모의 인덱스는 다음과 같다

부모의 인덱스 = (자식의 인덱스) / 2

힙 삽입 연산

새로운 노드를 힙의 마지막 노드에 삽입 후 새로운 노드를 부모 노드들과 교환해 힙 성질 만족시켜 재구성한다.

heap 크기 하나 증가 시킨다.
증가된 heap 크기 위치에 새로운 노드를 삽입한다.
i 가 루트 노드가 아니고 i 번째 노드가 i의 부모 노드보다 크면 i 번째 노드와 부모 노드를 교환한다.
한 레벨 위로 올라간다.

// 현재 요소의 개수가 heap_size인 히프 h에 item을 삽입한다. 

void insert_max_heap (HeapType* h, element item)
{
		int i ;
		i = ++(h->heap_size);
		
		// 트리를 거슬러 올라가면서 부모 노드와 비교하는 과정 
		while ((i != 1 ) && (item.key > h -> heap[i / 2].key)) {
				h -> heap[i] = h -> heap[i / 2];
				i /= 2 ; 
    }
		h -> heap[i] = item; // 새로운 노드 삽입 
}

힙 삭제 연산

최대 힙에서 삭제 연산은 최대값을 가진 요소(루트 노드)를 삭제하는 것이다. 루트 노드 삭제 후 히프를 재구성 하는 것이 필요하여 위, 아래 노드를 교환하는 작업이 필요하다.

루트 노드 값을 반환을 위해 item 변수로 옮긴다.
말단 노드를 루트 노드로 옮긴다.
heap 크기를 하나 줄인다.
루트의 왼쪽 자식부터 비교를 시작한다.
i가 히프트리의 크기보다 작다면, 두개의 자식 노드 중에서 큰 값의 인덱스를 largest로 옮긴다
largest이 부모 노드가 largest보다 크면 중지한다
그렇지않으면 largest와 largest의 부모 노드를 교환한 후 한 레벨 밑으로 내려간다.
최대값을 반환한다.

element delete_max_heap(HeapType *h)
{
		int parent, child;
		element item, temp;
		
		item = h -> heap[1];
		temp = h -> heap[(h -> heap_size)--];
		parent = 1;
		child = 2;
		while (child <= h-> heap_size) {
		// 현재 노드의 자식 중에서 더 큰 자식 노드를 찾는다.
		if ((child < h-> heap_size) &&
				(h-> heap[child].key) < h-> heap_size[child + 1].key)
				child++;
			// 한 단계 아래로 이동
			h -> heap[parent] = h -> heap[child];
			parent = child;
			child *= 2;
		}
		h-> heap[parent] = temp;
		return item;
}