추천시스템 입문하기 (1)

1. 컨텐츠 기반 모델

컨테츠 기반 추천시스템은 사용자가 이전에 구매한 상품 중 좋아하는 상품들과 유사한 상품들을 추천하는 방법이다.
➡️ 유사한 상품을 찾는 방법? :
1.1 (텍스트나 형태의)아이템들을 벡터 형태로 표현해서 찾은 후
1.2 벡터들간의 유사도를 계산해 유사한 벡터를 추출.

1.1 자연어처리 알고리즘

➡️ 텍스트나 형태의 아이템들을 벡터 형태로 표현하는 방법?
▶️ 자연어처리 알고리즘을 사용하여 벡터 형태로 표현한다.

1) TF-IDF

• TF-IDF는 특정 문서 내에 특정 단어가 얼마나 자주 등장하는 지를 의미하는 단어 빈도(TF)와 전체 문서에서 특정 단어가 얼마나 자주 등장하는 지를 의미하는 역문서 빈도(DF)를 통해 "다른 문서에서는 등장하지 않지만 특정 문서에서만 자주 등장하는 단어"를 찾아 문서 내 단어의 가중치를 계산하는 방법이다.

  $TF-IDF = TF * IDF$

• TF(term frequency) : 특정 문서 d에서 특정 단어 t의 출현빈도

• DF(document frequency) : 전체 문서 D에서 특정 단어 t가 등장한 문서 개수

• IDF(inverse document frequency) : DF값의 역수

• 빈도수를 기반으로 많이 나오는 중요한 단어들을 잡아주는 방법이 counter vectorizer인데 counter는 관사나 조사처럼 의미는 없지만 문장에 많이 등장하는 단어들도 높게 쳐주는 한계가 있다. 그러한 단어들에 패널티를 줘서 적절하게 중요 단어만을 잡아내는 기법이 TF-IDF 기법이다.

• TF-IDF는 전체 문서에서 빈출되는 단어의 중요도는 낮다고 판단하고, 특정 문서에서만 빈출되는 단어는 중요도가 높다고 판단한다.

➡️ TF-IDF 계산

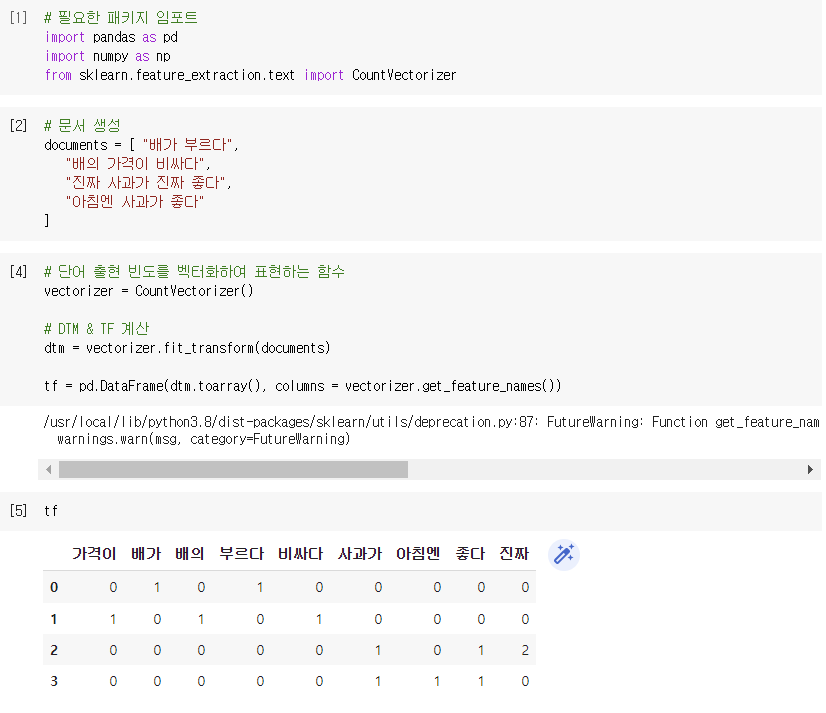
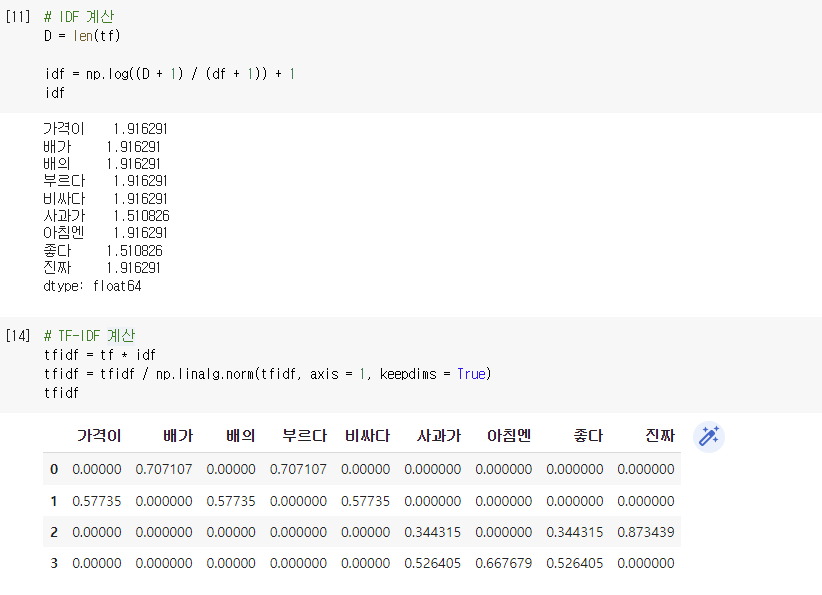
• 장점 : 직관적인 해석이 가능하다.
• 단점 : 대규모 말뭉치를 다룰 때 메모리상의 문제가 발생한다.

1.2 유사도 함수

➡️ 벡터들간의 유사도를 계산하는 방법?
▶️ 유사도 함수를 사용해서 벡터들간의 유사도를 (문서간의 유사도를) 계산한다.

1) 유클리디안 유사도

• 유클리디안 거리에 역을 취한 값으로 n차원 공간에서 두 점 사이의 최단 거리를 구하는 방법이다.
  
• 장점 : 계산하기 쉽다. (단순 거리만 구하면 됨)
• 단점 : P와 q의 분포나 범위가 다른 경우에 상관성을 놓치며 코사인 유사도에 비해 비교하는 문서 간 길이에 영향을 받는다.

2) 코사인 유사도

• 두 개의 벡터값에서 코사인 각도를 구하는 방법. -1 ~ 1 사이의 값을 가지며 1에 가까울수록 유사하다는 것을 의미한다.

  $cosine(X_r, X_s) = \frac{X_r \cdot X_s}{\parallel X_r \parallel \parallel X_s \parallel} = \frac{\sum_{i=1}^n X_{ri}X_{si}}{\sqrt{\sum_{i=1}^n X_{ri}^2}\sqrt{\sum_{i=1}^n X_{si}^2}}$

• 장점 : 코사인 유사도는 벡터 간 방향에 초점을 두기 때문에 문서의 길이가 다른 상황에서도 비교적 공정하게 유사도를 측정한다. (벡터의 크기가 중요하지 않은 경우에 거리를 측정하기 위한 메트릭이다.)

• 단점 : 벡터의 크기가 중요한 경우에 대해선 잘 작동하지 않는다.

3) 피어슨 유사도

• 두 벡터가 주어졌을 때의 상관관계를 계산하는 경우 많이 사용.

  $r_{rs} = \frac{\sum_{i=1}^n (X_{ri} - \overline{X_r}) (X_{si} - \overline{X_s})}{\sqrt{\sum_{i=1}^n (X_{ri} - \overline{X_r})^2}\sqrt{\sum_{i=1}^n (X_{si} - \overline{X_s})^2}}$

• 계산된 피어슨 유사도가 1이면 양의 상관관계, -1이면 음의 상관관계, 0이면 독립임을 의미한다.

4) 자카드 유사도

• 2개의 집합 A, B가 있을 때 두 집합의 합집합 중 교집합의 비율로 두 집합이 완전 같을 땐 자카드 유사도가 1이며 아예 다른 경우 0이다.

  $J(A, B) = \frac{|A \cap  B|}{|A \cup B|} = \frac{|A \cap B|}{|A| + |B| - |A \cap B|}$

• 다시말해 자카드 유사도는 하나의 집합을 문서로 보고 문서 간 단어 합집합의 원소 개수와 교집합의 원소 개수의 비율로 계산한다.

  $J(doc1, doc2) = \frac{doc1 \cap  doc2}{doc1 \cup doc2}$

• 즉 자카드 유사도는 특정 단어가 여러번 겹치는지는 고려하지 않고 얼마나 다른 종류의 단어가 겹쳤는지를 고려한다.