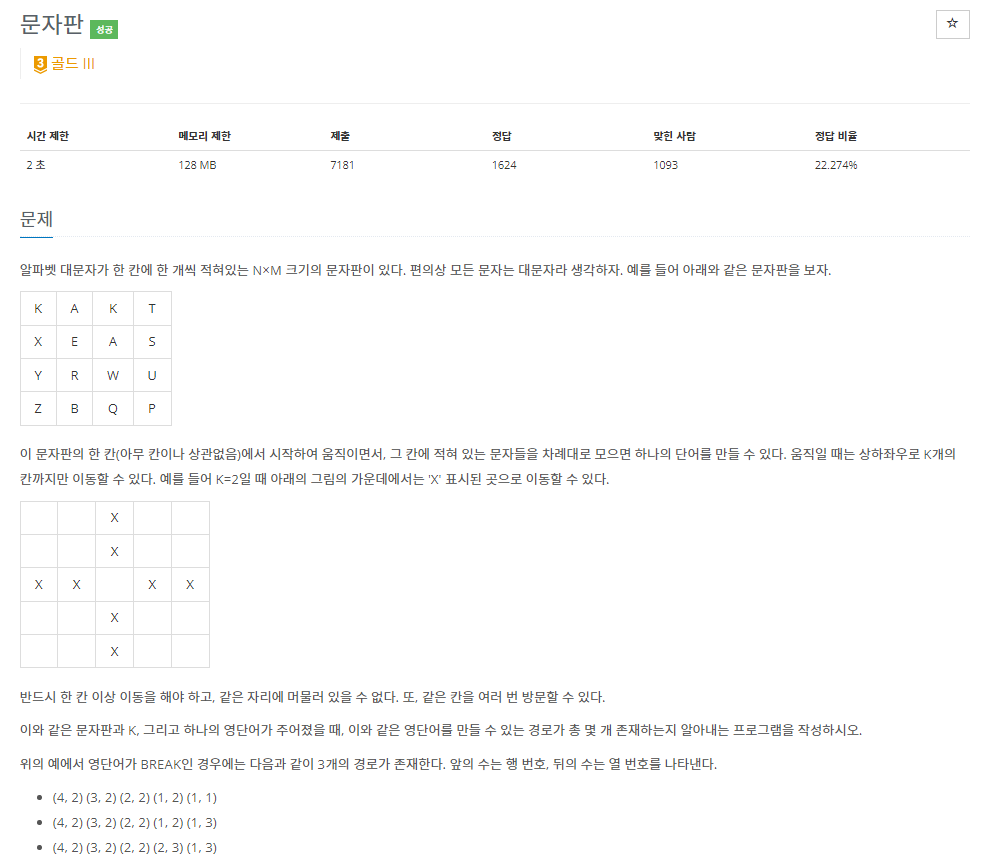
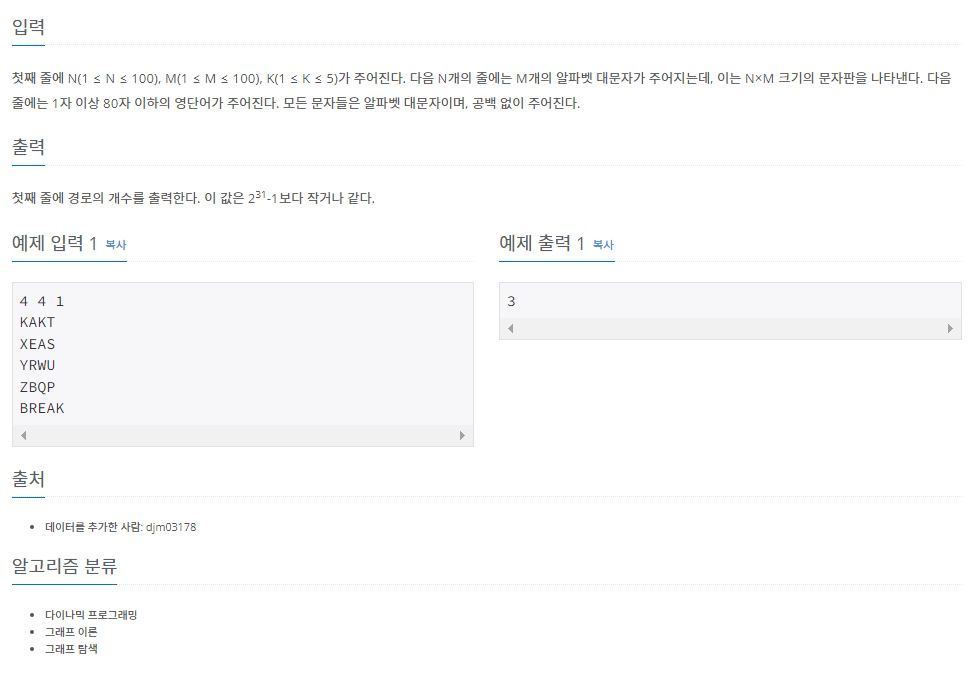
백준 2186번: 문자판

---

문제 접근법

문제를 읽어보고 미로 찾기와 비슷한 유형의 문제라고 생각하며 풀이를 진행했다.

처음 문제를 풀며 신경 쓴 부분은 다음과 같다.

1. 방향 배열 dx, dy를 만들어 {12시, 3시, 6시, 9시} 네 방향으로 향할 수 있도록 초기화하자.
   • 이때, 입력으로 주어지는 k를 통해 각 방향으로 k칸까지 갈 수 있도록 한다.
2. 일반적인 미로 찾기 문제와 다르게 최단경로를 찾는 문제가 아니니까 BFS가 아닌 DFS를 이용해서 해결해보자.
3. 방문했던 칸에 다시 한 번 더 방문할 수 있음을 인지하자! -> 중복 방지할 필요 없다.

실패..?

그렇게 DFS로 문제를 풀고 제출하였더니 시간 초과가 발생하여 실패했다..

생각해보니 주어지는 입력의 범위가 1 <= N,M <= 100 이고, 만들어야 되는 문자열의 길이가 80자까지 가능하므로 단순한 DFS로 해결하면 시간초과가 날 수 밖에 없다는 것을 깨달았다.

역시나 골드3 문제는 나에게 그렇게 호락호락하지 않았다.

시간초과를 해결하기 위한 시도

시간초과를 해결하기 위해, 한 방향으로 한 칸부터 시작해서 k칸까지 이동하는데 문자가 담겨있는 2차원 배열의 범윌을 벗어나게 되면 해당 방향으로 이동하는 반복문을 break하도록 코드를 짜봤다.

결과는 여전히 실패였다.

물론 약간의 반복 횟수를 줄일 수는 있겠지만 k의 범위가 1 <= k <= 5로, 애초에 작은 범위였다. 시간복잡도에 큰 영향을 미치는 요소는 위에서 언급한 입력 범위가 큰 N,M, 그리고 만들어야 되는 문자열이었다.

메모이제이션

이렇다 할만한 해결책을 찾지 못 하고 2시간정도를 고민하다가 accept 받은 코드를 참고하였다.

다른 개발자 분들은 모두 메모이제이션을 사용하여 이미 방문한 칸에 대해서 중복으로 방문하는 것을 방지하고 있는 것을 확인할 수 있었다.

내 '중복 방문을 방지할 필요가 없다'는 접근법 자체가 잘못됐다는 것을 깨달았다.

이 문제는 특정 문자열을 만들어갈 때, 그 문자열의 다른 인덱스에 대한 중복 방문을 허용하는 것이고, 같은 인덱스에 대한 중복 방문을 허용하지 않는다.

• 생각해보면 특정 조건이 있지 않은 이상, 같은 인덱스에 대한 중복 방문을 허용하면 무한 루프에 빠지게 되기 때문에 어떤 문제라도 이를 방지하며 문제를 해결하는 것이 당연하다.

결론은, 하나의 인덱스에 대해서 중복 방문이 일어나지 않도록 처리해줘야 된다!

코드

public class Main {
   static int n, m, k;
   static long cnt = 0;
   static char[][] board;
   static int[] dx = {-1, 0, 1, 0};
   static int[] dy = {0, 1, 0, -1};
   static int[][][] dp;
   static String answer;
   
   public static void main(String[] args) throws IOException {
      BufferedReader br = new BufferedReader(new InputStreamReader(System.in));

      StringTokenizer st = new StringTokenizer(br.readLine(), " ");

      n = Integer.parseInt(st.nextToken());
      m = Integer.parseInt(st.nextToken());
      k = Integer.parseInt(st.nextToken());

      board = new char[n][m];

      for (int i = 0; i < n; i++) {
         String input = br.readLine();
         for (int j = 0; j < m; j++) {
            board[i][j] = input.charAt(j);
         }
      }

      answer = br.readLine();
   }
}

BOJ에 올라온 예시를 그대로 활용해서 설명하도록 하겠다.

BufferedReader를 이용해서 변수를 입력받았다.
DFS 함수에서도 자유롭게 접근하기 위해서 static 변수로 선언했다. 문자를 하나씩 모으며 만들어야 되는 문자열을 answer라고 하자.

2차원 char 배열 board에 N x M 크기의 문자판을 저장했다.

문자판에서의 이동 방향을 가리키는 dx, dy 배열 또한 생성하였다. 4개의 인덱스는 0부터 3까지 각각 12시, 3시, 6시, 9시 방향을 가리킨다.

• 원리 : 기존의 좌표가 (x,y)일 때, x와 y에 각각 dx와 dy의 0번째 인덱스를 더하면 (x-1, y)가 되고, 이를 문자판에서 보면 위(12시 방향)로 한 칸 이동한 것과 같다.

그리고, 메모이제이션을 위한 dp 배열을 생성했다.
dp[x][y][L]이 가지는 의미는 다음과 같다.

dp 배열이 가지는 의미

: 문자판의 (x,y) 좌표에서부터 이동해서 answer의 L번 인덱스부터 끝까지 완성할 수 경우의 수

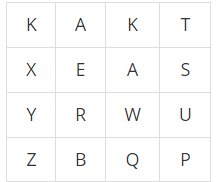
문자열 "BREAK"를 만들어야 되는 상황이다. 배열의 인덱스는 0부터 시작하고, k는 1이다. (백준 예시로 주어지는 입력과 완전히 같다.)

예시 1 (이동 가능한 좌표 중에 찾는 문자(L+1번 인덱스 문자)가 있는 경우)

dp[1][2][3]이 의미하는 것은, 문자판의 (1,2) 좌표에서부터 이동해서 "BREAK"의 3번 인덱스부터 끝까지 완성할 수 있는 경우의 수이다.

"BREAK" 문자열의 3번 인덱스~끝은 "AK"이다.
즉, (1,2) 좌표에서 이동해가며 "AK"를 만들 수 있는 경우의 수이다.

문자판의 (1,2) 좌표가 'A'를 가리키고 있으므로, 해당 좌표에서 'K'를 갈 수 있는 경우의 수가 dp[1][2][3]에 대입될 것이다.

(1,2) 좌표를 기준으로 {12시, 3시, 6시, 9시} 방향으로 한 칸씩 이동했을 때 'K'를 가리키는 좌표로 갈 수 있는 경우의 수는 12시 방향으로 이동했을 때 뿐이다.

결과적으로, dp[1][2][3] = 1 이 된다.

예시 2 (이동 가능한 좌표 중에 찾는 문자가 없는 경우)

dp[1][1][3]의 경우, 예시 1과 마찬가지로 "BREAK" 문자열의 3번 인덱스부터 끝, "AK"를 갈 수 있는 경우의 수를 찾아야 된다.

이제 좌표 (1,1)을 보자. 'E'를 가리키고 있다. "AK"를 완성해야 되기 때문에 L=3일 때, 'E'는 유효하지 않은 칸이 된다.

즉, dp[x][y][L]를 생각할 때, 좌표 (x,y)가 문자열 answer의 L번 인덱스 문자를 가리키고 있지 않다면, 유효하지 않은 칸이 되는 것이다.

이제, 이를 코드로 구현해보자.

dp = new int[n][m][answer.length()];

for (int i = 0; i < n; i++) {
   for (int j = 0; j < m; j++) {
       Arrays.fill(dp[i][j], -1);
   }
}

문자판(n x m)을 문자열의 인덱스 별로 체크할 것이기 때문에, dp 배열의 크기는 [n][m][answer.length()]가 된다.

위 예시에서 두 가지 경우를 봤다.
1. 문자열을 완성하는 것이 가능하다고 판단되는 경우(유효한 경우)
2. 문자열을 완성하지 못하는 경우(유효하지 않은 경우)

여기에 한 가지 경우가 더 있다. 아직 방문하지 않은 경우이다.

이렇게 총 3가지 경우를 dp 배열에 표현하기 위해 -1, 0, 1로 나눈다.

• -1 : 방문하지 않은 경우
• 0 : 유효하지 않은 경우
• 1 : 유효한 경우

기본은 방문하지 않은 경우이기 때문에 dp 배열을 -1로 채운다.

이제 dp 배열을 채워가며 DFS를 실행해보자.

public static int DFS(int x, int y, int L) {
    if (dp[x][y][L] != -1) return dp[x][y][L];
    if (L == answer.length()-1) return dp[x][y][L] = 1;

    dp[x][y][L] = 0;

    for (int i = 1; i <= k; i++) {
        for (int j = 0; j < 4; j++) {
            int nx = x + dx[j] * i;
            int ny = y + dy[j] * i;

            if (nx < 0 || ny < 0 || nx >= n || ny >= m) continue;

            if (board[nx][ny] == answer.charAt(L+1)) dp[x][y][L] += DFS(nx, ny, L + 1);
        }
    }
    return dp[x][y][L];
}

1. 이미 방문했던 칸에 대해서는 기록하기 위해 기본으로 -1로 채워놨던 dp 배열의 값을 0으로 바꾼다.

기본적으로 DFS 함수에서 방문한 좌표에 대해 dp 배열의 값을 0으로 세팅하기 때문에, dp[x][y][L] != -1 이라는 것은 이미 방문했던 칸이라는 것이다. 이 경우에는 그대로 return 하며 같은 인덱스에 대해 이미 방문했던 칸을 방문하지 않도록 한다.

L == answer.length() -1 의 경우, 마지막에 설명하도록 하겠다.

2. 반복문을 통해 dx와 dy 배열을 돌면서 4가지 방향을 각각 1~k칸씩 이동했을 떄의 좌표인 (nx, ny)가 유효한 칸인지 검사한다.

   • 첫 번째로, (nx, ny)가 2차원 배열 board의 범위를 벗어나지 않는지 확인한다.
   • 두 번째로, (nx, ny)가 L+1번째, 즉 다음 인덱스의 문자인지 검사한다. 이는 현재 좌표인 (x,y)에서 다음 문자를 찾아갈 수 있는지 확인하는 것이다.
     • 위 예시 1을 보면, 'A'에서 네 방향을 돌며 다음 문자인 'K'가 있는 칸에 갈 수 있는지 확인하는 과정과 같다.

3. 확인 결과, 다음 인덱스 문자에 도달할 수 있다면, 인덱스(L)를 증가시키며 (nx,ny) 좌표로 이동하며 위 과정을 반복한다.

4. 인덱스(L)를 증가시키면서 재귀 호출을 진행하다가, L == answer.length() -1 즉, 문자열의 길이만큼 인덱스를 구하면 문자열을 완성한 것이다. 문자열을 완성했으므로, 1을 return 하여 지금까지 거쳐온 좌표들의 dp 값에 1씩 더해주도록 한다.

dp 배열을 완벽히 이해해보자

위 과정을 반복하면, dp[x][y][0]에는 (x,y) 좌표에서 시작해서 문자열을 완성할 수 있는 경우의 수가 쌓이게 된다.
dp[x][y][0]에 값이 들어오는 과정은 뒤 인덱스에서부터 확인하면 알기 쉽다.

dp[x][y][3]

• board[x][y] == 'A'(유효) : (x,y)에서 'K'로 갈 수 있는 경우의 수 -> dp[nx][ny][4] = 1
  • board[nx][ny] == 'K'인 (nx,ny) 쌍의 수만큼 경우의 수가 증가하는 것이다.
• board[x][y] != 'A' : 0

dp[x][y][2]

• board[x][y] == 'E' : (x,y) 에서 "AK"로 갈 수 있는 경우의 수 -> dp[nx][ny][3] + dp[nnx][nny][4];
  • 이때, board[nx][ny] == 'A' , board[nnx][nny] == 'K'
• board[x][y] != 'E' : 0

dp[x][y][1]

• board[x][y] == 'R' : (x,y) 에서 "EAK"로 갈 수 있는 경우의 수 -> dp[nx][ny][2] + dp[nnx][nny][3] + dp[nnnx][nnny][4];
  • 이때, board[nx][ny] == 'E' , board[nnx][nny] == 'A', board[nnnx][nnny] == 'K'
• board[x][y] != 'R' : 0

dp[x][y][0]

• board[x][y] == 'B' : (x,y) 에서 "REAK"로 갈 수 있는 경우의 수 -> dp[nx][ny][1] + dp[nnx][nny][2] + dp[nnnx][nnny][3] + dp[nnnnx][nnnny][4];
  • 이때, board[nx][ny] == 'R' , board[nnx][nny] == 'E', board[nnnx][nnny] == 'A', board[nnnnx][nnnny] == 'K'
• board[x][y] != 'B' : 0

이렇게 뒤 인덱스에서부터 다음 인덱스에 도달할 수 있는 경우의 수가 쌓이고, dp[x][y][0]에 쌓인 경우의 수가 들어오게 되는 것이다.

그리고, 우리는 (x,y)에서 갈 수 있는 유효한 좌표인 (nx,ny)를 DFS를 통해 모든 경우의 수를 검사하며 찾게 되는 것이다.

위 설명에서의 (nx, ny)는 (x,y)에서 DFS를 통해 찾은 다음 인덱스의 유효한 좌표이고, (nnx, nny)는 (nx, ny)에서 DFS를 통해 찾은 다음 인덱스의 유효한 좌표이다.

for (int i = 0; i < n; i++) {
    for (int j = 0; j < m; j++) {
        if(board[i][j] == answer.charAt(0)) cnt += DFS(i, j, 0);
    }
}

System.out.println(cnt);

DFS(x,y,L)에서, (x,y) 좌표가 가리키는 문자가 "BREAK"의 시작 문자인 'B'가 아니라면 어차피 유효하지 않은 칸이기 때문에 dp 배열에 0만 할당하고 바로 종료될 것이다.

그렇기 때문에, 'B'를 가리키는 좌표를 모두 찾아 그 좌표에서부터 DFS 함수를 실행한다.

'B'를 가리키는 좌표 (a,b)에서의 DFS 재귀 호출이 모두 종료되면, 위에서 설명한 것처럼 dp[a][b][0]에는 (a,b)에서 이동하며 모든 인덱스를 채우는 경우의 수가 할당될 것이다.

'B'를 가리키는 모든 좌표의 dp 값을 합치면 우리가 구하고자 했던 값, 전체 문자판에서 "BREAK"를 완성할 수 있는 경우의 수가 구해진다.

완성 코드

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Arrays;
import java.util.StringTokenizer;

public class Main {
    static int n, m, k;
    static long cnt = 0;
    static char[][] board;
    static int[] dx = {-1, 0, 1, 0};
    static int[] dy = {0, 1, 0, -1};
    static int[][][] dp;
    static String answer;

    public static int DFS(int x, int y, int L) {
        if (dp[x][y][L] != -1) return dp[x][y][L];
        if (L == answer.length()-1) return dp[x][y][L] = 1;

        dp[x][y][L] = 0;

        for (int i = 1; i <= k; i++) {
            for (int j = 0; j < 4; j++) {
                int nx = x + dx[j] * i;
                int ny = y + dy[j] * i;

                if (nx < 0 || ny < 0 || nx >= n || ny >= m) continue;

                if (board[nx][ny] == answer.charAt(L+1)) dp[x][y][L] += DFS(nx, ny, L + 1);
            }
        }
        return dp[x][y][L];
    }

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));

        StringTokenizer st = new StringTokenizer(br.readLine(), " ");

        n = Integer.parseInt(st.nextToken());
        m = Integer.parseInt(st.nextToken());
        k = Integer.parseInt(st.nextToken());

        board = new char[n][m];

        for (int i = 0; i < n; i++) {
            String input = br.readLine();
            for (int j = 0; j < m; j++) {
                board[i][j] = input.charAt(j);
            }
        }

        answer = br.readLine();
        dp = new int[n][m][answer.length()];

        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++) {
                Arrays.fill(dp[i][j], -1);
            }
        }

        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++) {
                if(board[i][j] == answer.charAt(0)) cnt += DFS(i, j, 0);
            }
        }

        System.out.println(cnt);
    }
}

---

회고

고작 알고리즘 한 문제에 대해 이렇게 열심히 작성하고, 회고를 하게 될 줄은 몰랐지만, 이 문제는 날 너무나도 괴롭혀서 남다르게 느껴진다.

혼자 해결하기 위해 고민을 하다가 도저히 모르겠어서 accept 받은 코드를 보게 됐는데, 코드를 보고도 이해가 되지 않아서 너무 답답했고, 어떻게든 이해하고 말겠다는 생각을 했다.

여러명의 정답 코드를 봐도 메모이제이션이 이해가 되지 않았고, DFS 함수가 재귀호출되며 스택에 쌓이는 과정, 3차원인 dp 배열이 채워지는 과정을 직접 손으로 그려가며 겨우겨우 '왜 작동하는지'는 이해하게 되었다.

앞으로 이와 비슷한 문제에 대해서 효율적인 방법으로 접근하기 위해서는 완벽한 이해가 필요하다고 느꼈고, 코드의 모든 과정에 대해 최대한 자세히 설명하며 부족한 이해도를 채워야겠다고 생각하며 이 글을 작성하게 되었다.

결국엔 문제의 핵심을 관통하는 깔끔하고 명쾌한 문제풀이 포스팅이 아니라, 불필요한 부분까지도 설명했다고 생각이 들 정도로 주저리주저리 써놓은 글이 되었다.(설명충)

하지만, 글을 쓰며 계속해서 문제에 대해 생각하고 더욱 깊게 이해하게 되어서 1차 목표는 달성했다.

알고리즘 공부를 열심히 해야겠다는 생각은 자주 하지만, 그 어느때보다 자극을 준 문제였다. 열심히 공부해야겠다.