최소 공통 조상(LCA, Lowest Common Ancestor)

yujamint·2025년 4월 7일
ps
0

PS

목록 보기
11/11
post-thumbnail

개념

트리가 주어졌을 때, u와 v 두 노드의 조상이면서 가장 깊은 노드를 찾는 알고리즘이다.

예를 들어, 아래와 같은 트리가 존재한다고 가정하자. 4번 노드와 6번 노드의 공통 조상은 1번 노드, 2번 노드가 존재한다. 1번 노드는 루트 노드로, 깊이가 0이고 2번 노드는 깊이가 1이다. 따라서 가장 깊은 2번 노드가 최소 공통 조상이다.

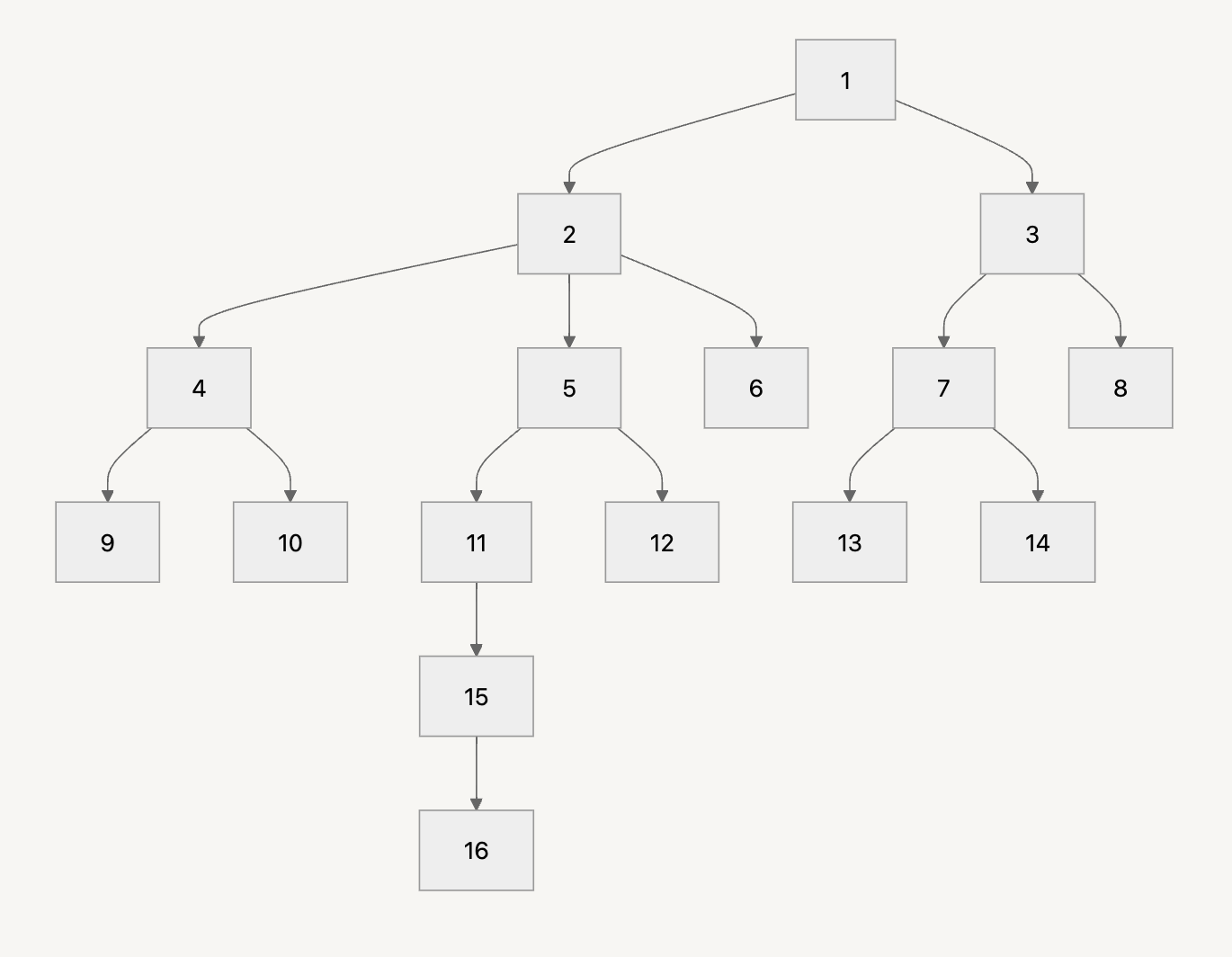
어떻게 찾을까?

기본적인 아이디어는 다음과 같다.

  1. 높이 맞추기: 낮은 깊이를 기준으로, u와 v의 깊이가 같아지도록 한다.
  2. 최소 공통 조상 찾기: u와 v가 같아질 때까지 각각의 부모 노드로 이동한다. (= 높이를 올린다.)
  3. u와 v가 같아지는 첫 노드가 최소 공통 조상이다.

위에서 사용한 트리를 기준으로 8번 노드와 15번 노드의 최소 공통 조상을 찾아보자.

  1. 15 → 11 → 5
    • 8번 노드의 깊이는 2, 15번 노드의 깊이는 4이다. 따라서 15번 노드의의 깊이를 2가 되도록 맞춰야 한다.
    • 따라서 부모 노드로 2번 이동한다.
  2. 5 → 2 → 1 / 8 → 3 → 1
    1. 5 ≠ 8 → 각각의 부모 노드로 이동 u = 2 / v = 3
    2. 2 ≠ 3 → 각각의 부모 노드로 이동 u = 1 / v = 1
    3. 1 = 1
  3. u와 v가 1로 같아졌다. 8번 노드와 15번 노드의 최소 공통 조상은 1이다.

시간복잡도 문제

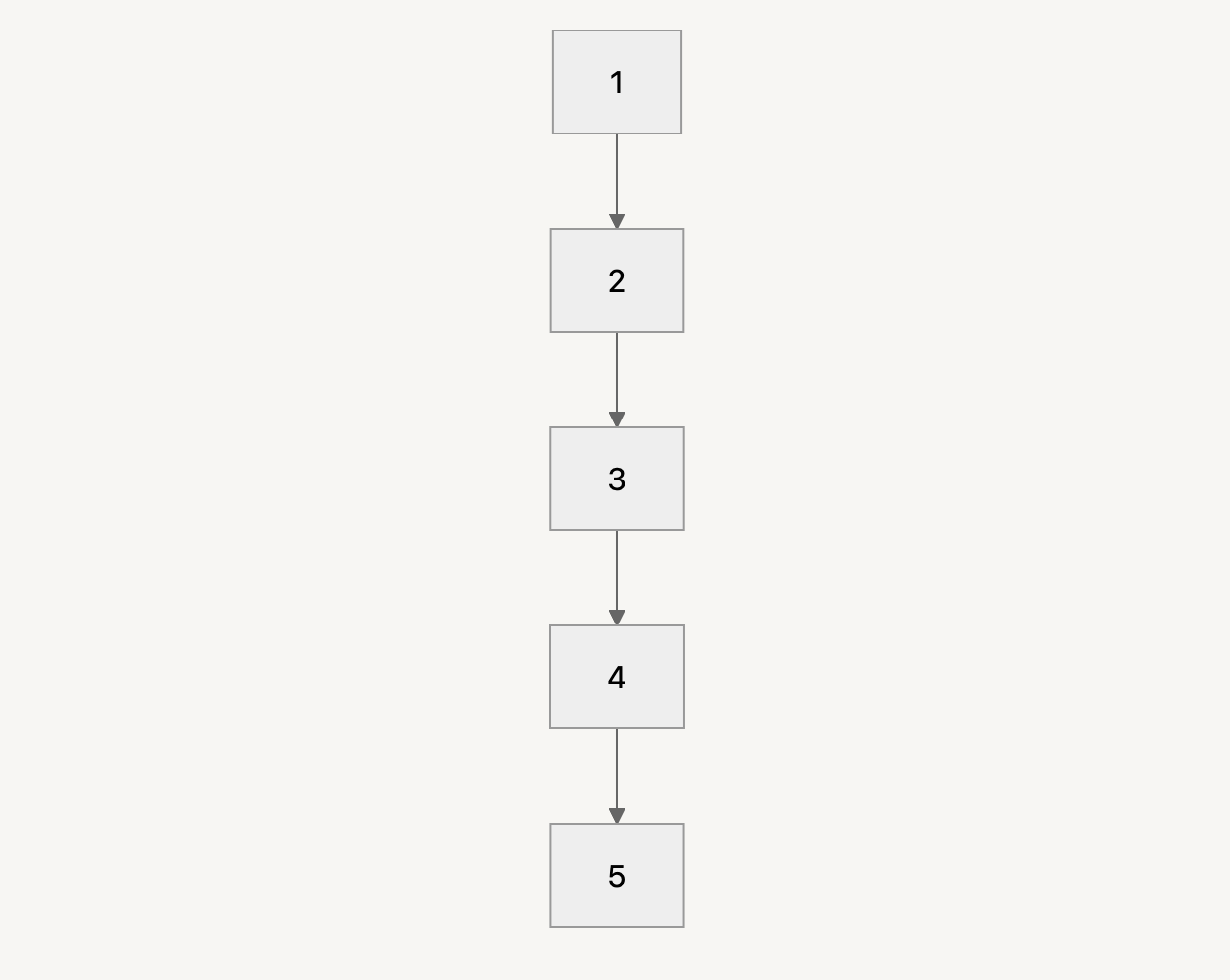
위 방식에서는 1번과 2번 과정에서 모두 부모 노드로 한 번씩 이동한다. 이는 O(n)의 시간복잡도를 갖게 된다. 아래의 트리에서 1번 노드와 5번 노드의 최소 공통 조상을 찾는 것을 예로 생각해보자.

1번 노드와 5번 노드의 깊이를 맞추기 위해 5번 노드를 부모 노드로 4번 이동해야 한다. 이는 n-1번의 연산이 필요함을 의미한다. 따라서 한 번씩 부모 노드로 이동하는 것은 상당히 느리다.

최적화

희소 테이블의 개념을 사용해서 이를 O(log n)의 시간복잡도로 최적화할 수 있다.

다시 위의 트리를 가져와서 8번 노드와 16번 노드의 최소 공통 조상을 찾아보자.

높이 맞추기

8번 노드와 16번 노드의 깊이 차이는 3이다. 차이를 이진수로 나타내면 11(2)이다. 우리는 이진수로 표현한 깊이 차이를 통해 한 번에 한 칸씩 이동하는 게 아니라, 2^k칸씩 이동할 것이다.

11(2)라는 깊이 차이가 주어졌을 때, 하나의 비트씩 확인하며 이동하는 것이다. 높은 자리의 비트부터 확인한다고 하면 2^1칸 이동, 2^0칸 이동하여 총 2번의 이동으로 3칸을 이동한다.

이렇게 O(n)의 시간복잡도로 높이를 맞추던 과정을 O(log n)으로 최적화했다.

최소 공통 조상 찾기

이제 16은 높이를 맞추며 5가 되었고, 5와 8이 같아질 때까지 부모 노드로 이동해야 한다. 이때도 우리는 비트를 통해 O(log n)의 시간복잡도로 최소 공통 조상을 찾을 수 있다.

최소 공통 조상이 1이라는 결과를 먼저 알고 있는 상태에서 보면 두 노드와 최소 공통 조상의 높이 차이는 2이므로, 2번 이동해야 한다. 이를 이진수로 나타내면 10(2)이다. 따라서 1칸씩 2번이 아니라 2칸씩 1번 이동하면 된다. 이는 높이 맞추기에서 최적화한 희소 테이블의 원리와 같다.

  • 최소 공통 조상까지의 높이 차이가 10이라면 1010(2)이다. 따라서 8칸 1번, 2칸 1번 이동한다.
  • 최소 공통 조상까지의 높이 차이가 512라면 1000000000(2)이다. 따라서 512칸 1번 이동한다.

즉, 최소 공통 조상과의 높이 차이만큼 2^k 꼴로 이동하며 O(log n)의 시간복잡도로 이동할 수 있다. 다만 우리는 최소 공통 조상과의 높이 차이를 모른다. 따라서 가능한 최대 자리의 비트부터 확인하며 최소 공통 조상을 찾는다.

예를 들어, 노드가 총 50,000개 있다고 가정하자. 이떄 가능한 트리의 최대 높이 또한 50,000이다. 이는 16개의 비트를 사용해서 표현할 수 있다. (50,000 ≤ 2^k - 1을 만족하는 가장 작은 수가 16이다.)
그러면 우리는 2^15 자리부터 2^0자리까지 확인하며 최소 공통 조상을 찾을 것이다. 과정은 다음과 같다.

  1. k = 15 ; k ≥ 0; k—

  2. u와 v에서 2^k번째 부모로 이동할 수 있는지 확인한다.

    만약 u와 v의 깊이가 2라면 4,8,16,…,2^15번째 부모는 존재하지 않기 때문에 이동할 수 없다.

  3. u와 v의 2^k번째 부모가 같지 않은지 확인한다.

    부모가 같다는 것은 공통 조상임을 의미하지만, 최소 공통 조상은 아닐 수 있다. 우리는 높은 자리의 비트부터 확인하기 때문에 깊이가 낮은 조상으로 이동하게 되는 문제가 생길 수 있다.
    u와 v의 1023번째 조상이 최소 공통 조상이라면, 2^10 자리 이상의 비트를 사용하는 순간 1023보다 커지기 때문에 최소 공통 조상을 넘어가게 된다.

  4. 1번, 2번 조건을 만족한다면 각각 2^k번째 부모로 이동한다.

  5. 2~4번 과정을 반복한다.

이 과정을 반복하면 u와 v의 부모는 각각 같은 노드를 가리키고 있으며, 그 노드가 곧 최소 공통 조상이 된다.

노드가 총 50,000개 있다고 가정했을 때 16개의 비트를 사용해서 표현할 수 있다고 했다. 이는 곧, 최대 16번의 연산으로 최소 공통 조상을 찾을 수 있음을 의미한다.

희소 테이블?

높이를 맞추는 과정과 최소 공통 조상을 찾는 과정에서 모두 O(n)의 시간복잡도를 갖는 과정을 희소 테이블의 개념을 사용하여 O(log n)의 시간복잡도로 최적화했다. 다시 정리하자면, 한 번씩 이동하는 게 아니라 2^k번 꼴로 이동함으로써 연산 횟수를 줄인 것이다.

하지만 문제에서 u의 2^k번째 부모가 무엇인지 알려줄 리는 없기 때문에 특정 노드의 2^k번째 부모가 무엇인지 미리 찾아 놓는 전처리 과정이 필요하다. 이 과정이 희소 테이블을 만드는 것이다. 전처리 과정은 바텀업 DP를 통해 가능하다.

parent[i][j] = i 노드의 2^j번째 부모

  1. 문제에서 주어진 간선과 루트 노드 번호를 통해 각 노드의 첫 번째 부모를 알 수 있다. (= parent[i][0])

  2. 노드 u의 두 번째 부모는 곧 u의 첫 번째 부모의 첫 번째 부모이다.

    → parent[u][1] = parent[parent[u]][0]

  3. 노드 u의 네 번째 부모는 곧 u의 두 번째 부모의 두 번째 부모이다.

    → parent[u][2] = parent[parent[u]][1]

  4. 노드 u의 2^k번째 부모는 곧 u의 2^(k-1)번째 부모의 2^(k-1)번째 부모이다.

    → parent[u][k] = parent[parent[u]][k - 1]

일반화하는 과정을 보면 알 수 있듯이 2^k = 2^(k-1) * 2^(k-1)임을 활용한 전처리 과정이다.

노드의 개수가 n이고 n의 범위를 커버할 수 있는 가장 작은 비트 수가 k개라고 할 때, 전처리 과정 시간복잡도는 O(nk)이다. 이때 k는 n을 이진수로 나타냈을 때의 비트 수와 같기 때문에 log n으로 치환이 가능하다. 따라서 O(n logn)의 시간복잡도를 갖는다.

위에서 언급한 희소테이블은 2^k번째 부모를 저장하는 방식이다. 만약 2^k 꼴이 아니라 첫 번째 부모, 두 번째 부모, …, n번째 부모를 모두 저장하는 방식으로 전처리를 구성한다면 최소 공통 조상을 찾는 과정이 O(1)으로 해결될 것이다. 하지만 이는 전처리 과정의 시간복잡도가 O(n^2)이 될 뿐 아니라 메모리까지 그만큼 많이 사용하게 된다.

관련 문제 (BOJ 11438)

백준 온라인 저지의 11438번 문제(LCA 2)를 예제로 풀었다.

#include <iostream>
#include <vector>
#include <memory.h>

using namespace std;

const int MAX = 100000;
const int MAX_D = 17;

int n, m;
vector< vector<int> > graph;
int depth[MAX];
int parent[MAX][MAX_D];

void makeTreeByDFS(int cur) {
    for (int next : graph[cur]) {
        if (depth[next] == -1) {
            parent[next][0] = cur;
            depth[next] = depth[cur] + 1;
            makeTreeByDFS(next);
        }
    }
}

int main() {
    ios::sync_with_stdio(false);
    cout.tie(nullptr);
    cin.tie(nullptr);

    cin >> n;

    graph = vector< vector<int> >(n, vector<int>());
    for (int i = 0; i < n - 1; ++i) {
        int a, b;
        cin >> a >> b;
        a--; b--;
        graph[a].push_back(b);
        graph[b].push_back(a);
    }

    memset(parent, -1, sizeof(parent));
    memset(depth, -1, sizeof(depth));
    depth[0] = 0;
    // 트리 생성
    makeTreeByDFS(0);

    // parent 배열 채우기
    for (int j = 0; j < MAX_D - 1; ++j) {
        for (int i = 1; i < n; ++i) {
            if (parent[i][j] != -1)
                parent[i][j + 1] = parent[parent[i][j]][j];
        }
    }

    cin >> m;
    for (int i = 0; i < m; ++i) {
        int a, b;
        cin >> a >> b;
        a--; b--;
        if (depth[a] < depth[b]) swap(a, b);
        int diff = depth[a] - depth[b];

        for (int j = 0; diff; ++j) {
            if (diff % 2) a = parent[a][j];
            diff /= 2;
        }

        if (a != b) {
            for (int j = MAX_D - 1; j >= 0; --j) {
                if (parent[a][j] != -1 && parent[a][j] != parent[b][j]) {
                    a = parent[a][j];
                    b = parent[b][j];
                }
            }
            a = parent[a][0];
        }

        cout << a + 1 << '\n';
    }

    return 0;
}

References

https://blog.naver.com/PostView.naver?blogId=kks227&logNo=220820773477&categoryNo=299&parentCategoryNo=0&viewDate=¤tPage=2&postListTopCurrentPage=1&from=postList&userTopListOpen=true&userTopListCount=15&userTopListManageOpen=false&userTopListCurrentPage=2

profile
yujamint
개발 기록
이전 포스트

분할 상환 분석이란 (Amortized Analysis)

0개의 댓글