BinarySearch 이진탐색

유정현·2024년 4월 5일

개요

오늘 완전 탈탈 털렸다. 이진탐색 내가 제일 싫어한다. 인덱싱하는게 정말 귀찮고 예민하다. 그냥 틀만 짜면 잘 굴러가는 DFS가 훨씬 사랑스럽고, 적당히 괜찮아 보이는 방법 쓰면 정답 나오는 그리디가 행복하다. 근데 오늘 털렸는데 어떡해 공부해야지 이번엔 털어줘야겠다.

이진탐색

소주병 뚜껑, 맥주병 뚜껑, 배스킨라빈스31 업다운 게임같은 거다. 정렬된 배열에서 중간 지점을 계속해서 내가 원하는 것이 나올 때까지 탐색해나가는 방법이다.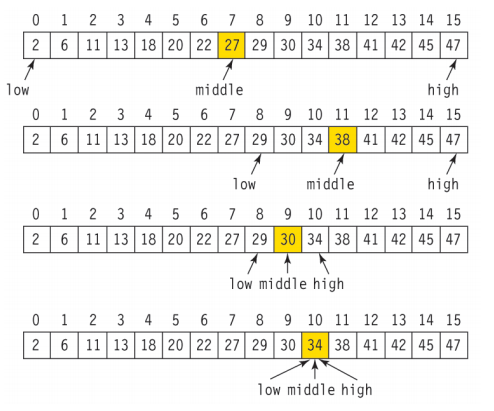
이런 문제다. 그래서 코드로 쓰면 아래와 같다. 시작지점과 끝지점을 정하고, 그 중간을 계속해서 탐색해나간다. 나는 사실 이 while문 보다는 재귀풀이가 좀 더 익숙하다... 처음에 배운게 그래서 그런가. 암튼 그래서 이 다음 코드는 재귀로 작성한 코드다.
while

long left = 0;
long right = maxTreeHeight;
long result = 0;

while (left <= right) {
     long mid = (left + right) / 2;
     long totalLength = 0;

     for (long tree : trees) {
          if (tree > mid) {
              totalLength += tree - mid;
          }
     }

     if (totalLength >= M) {
          result = mid;
          left = mid + 1;
     } else {
          right = mid - 1;
     }
 }

재귀풀이

 static long result = 0;
    public static long biSearch(long lt, long rt, long mid, long goal) {
        long treeLen = treeLen(mid);

        if(lt > rt){
            return result;
        }
        if(treeLen >= goal){
            result = mid;
        }

        if(treeLen < goal){
            return biSearch(lt, mid-1, (mid - 1 + lt)/2, goal);
        } else {
            return biSearch(mid + 1, rt, (mid + 1 + rt)/2, goal);
        }
    }

재귀와 while문의 차이

사실 그렇게 큰 차이는 없는 것 같다. DFS도 사실 재귀 써도 되고 안 써도 풀 수 있는데 재귀 써도 다 잘 풀리는거 보면 성능상 그렇게 엄청 큰 차이는 없는 것 같다. 다만 경우에 따라서 코드의 길이가 훨씬 짧아지기도 길어지기도 하는데 위 문제와 같은 경우에는 while문이 더 깔끔했다. 보통 조건이 저렇게 여러가지가 아닌 상황에서는 재귀풀이가 조금 더 깔끔한 느낌이 든다.

재귀풀이의 오버헤드

스택 프레임을 가상머신에서 사용하는 언어들은 재귀풀이에 오버플로우가 날수도 있다. 요즘 쓰는 거의 모든 언어가 스택프레임 기반이므로, 코테에서나 쓰고 다른데서는 쓰지말자. 난 그냥 사고가 이게 익숙해져서 이걸 좀 고집해서 쓰고있다.

시간복잡도

시간 복잡도는 O(logN)이다. 항상 반으로 나눠서 탐색하기 때문에 일반적인 선형탐색보다 훨씬 빠르다. 대신에 메모리는 더 많이 든다.

빅오 표기법

빅오 표기법은 주어진 문제에서 나오는 연산 대상의 갯수와 해당 연산과 관련이 있다. 일반적으로 100000개의 원소를 정렬하는데 버블정렬이나 삽입 정렬 같은 경우 최악의 경우 O(N^2)이 되는 것이다. 이게 사실 겉으로 보면 크게 중요해보이지 않은데 문제가 점점 어려워질 수록 생각하는게 좋다.
왜냐하면 문제가 어려워진다는 건 코드가 길어진다는 것이고, 코드가 길어진다는 것은 그 문제를 풀기 위해 설계가 필요하다는 것이다. 내가 생각하는 전략을 빅오표기법으로 생각했을 때 조건에 맞는지 확인하면서 진행하는게 좋다.