S-DES(Simplified Data Encryption Standard)

박유란·2023년 10월 5일

컴퓨터보안

목록 보기

1/1

<알고리즘>

Input: 8-bit 평문(Plaintext), 10-bit Key
Output: 8-bit 암호문(Ciphertext)
Round: 2

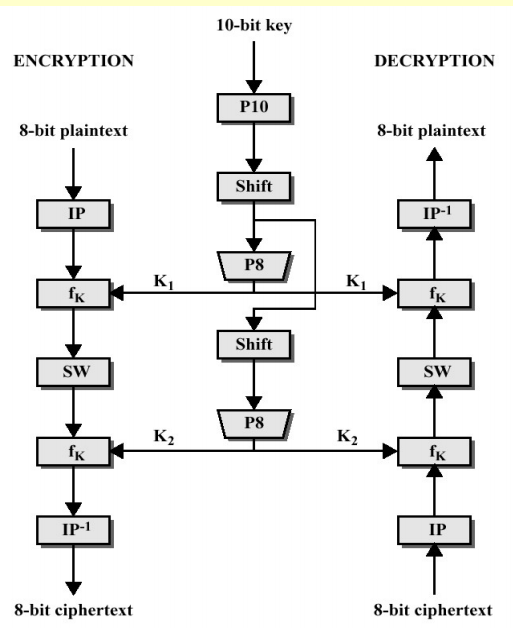
Encrytion 수식
$E = IP^{-1}(f_{k2}(SW(f_{k1}(IP(M)))))$
Decrytion 수식
$M = IP^{-1}(f_{k1}(SW(f_{k2}(IP(E)))))$

<예제>

Input

평문(8-bit)

0	1	1	1	0	1	1	0

Key(10-bit)

1	1	1	0	0	0	1	0	0	1

1) Key(10-bit)값으로 (K1, K2) 생성

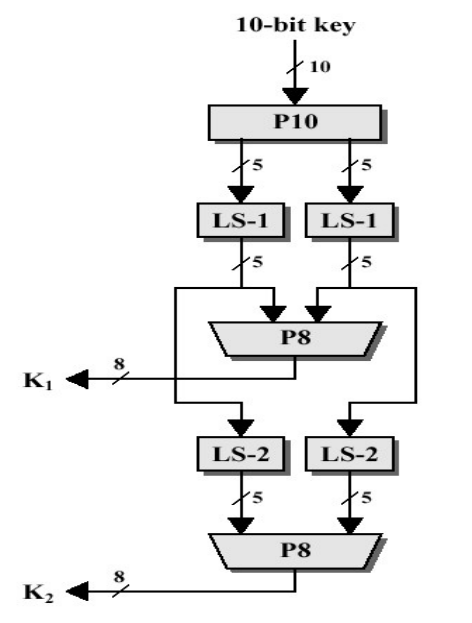
① 순열(P10)

P10
3 5 2 7 4 10 1 9 8 6

☑️ Input(10-bit) :

1	1	1	0	0	0	1	0	0	1
1	2	3	4	5	6	7	8	9	10

☑️ Output(10-bit) :

비트열을 P10에 적용하여 순열 변환

1	0	1	1	0	1	1	0	0	0
3	5	2	7	4	10	1	9	8	6

②-(1) 5-bit 단위로 Shift연산(LS-1)

☑️ Input(10-bit) :

1	0	1	1	0	1	1	0	0	0

☑️ Output(10-bit) :

1~5비트 -> 1-bit 좌순환 연산(Left-Shift)

0	1	1	0	1

6~10비트 -> 1-bit 좌순환 연산(Left-Shift)

1	0	0	0	1

②-(2) 순열(P8): k1 생성

P8
6 3 7 4 8 5 10 9

☑️ Input(10-bit) :

입력된 비트열 중 8-bit를 선택하여 P8 순열 변환

0	1	1	0	1	1	0	0	0	1
1	2	3	4	5	6	7	8	9	10

☑️ Output(8-bit) :

k1 생성 결과

1	1	0	0	0	1	1	0
6	3	7	4	8	5	10	9

③-(1) Shift연산(LS-2)

☑️ Input(10-bit) :
*LS-1한 후 output을 입력으로 함

0	1	1	0	1	1	0	0	0	1

☑️ Output(10-bit) :

1~5비트 -> 2-bit 좌순환 연산(Left-Shift)

1	0	1	0	1

6~10비트 -> 2-bit 좌순환 연산(Left-Shift)

0	0	1	1	0

③-(2) 순열(P8): k2 생성

P8
6 3 7 4 8 5 10 9

☑️ Input(10-bit) :

1	0	1	0	1	0	0	1	1	0
1	2	3	4	5	6	7	8	9	10

☑️ Output(8-bit) :

k2 생성 결과

0	1	0	0	1	1	0	1
6	3	7	4	8	5	10	9

2) 암호화 과정

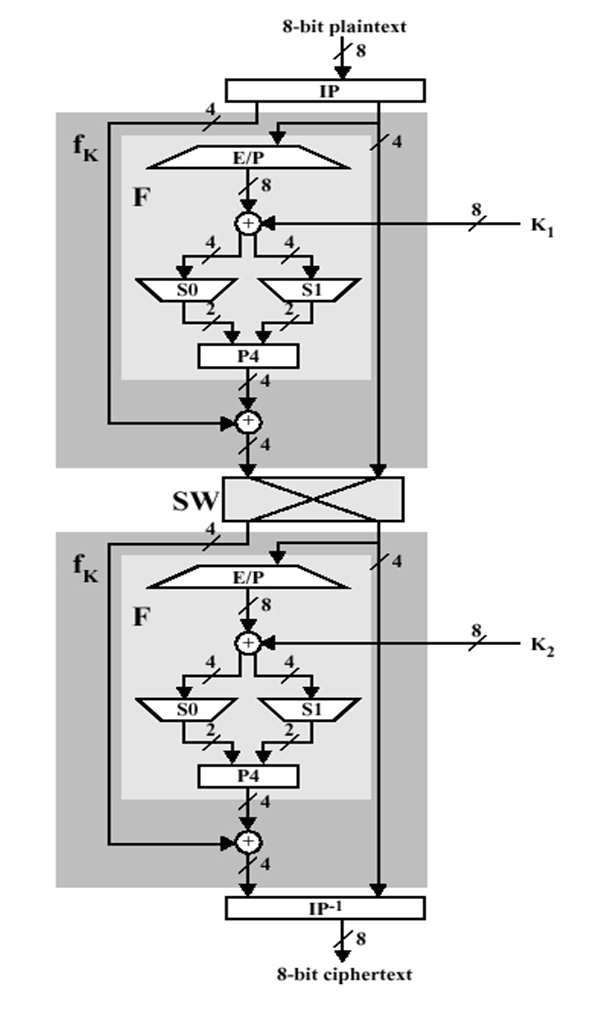
▶️ ROUND 1

평문 :

0	1	1	1	0	1	1	0

k1 :

1	1	0	0	0	1	1	0

① 초기순열(IP)

$IP$
2 6 3 1 4 8 5 7

☑️ Input(8-bit) :

0	1	1	1	0	1	1	0

☑️ Output(8-bit) :

1	1	1	0	1	0	0	1
2	6	3	1	4	8	5	7

② 4-bit 단위로 $L_{0}$ 블록과 $R_{0}$ 블록으로 나눔

☑️ $L_{0}$ (4-bit) :

1	1	1	0

☑️ $R_{0}$ (4-bit) :

1	0	0	1

③ $R_{0}$ 블록(4-bit) 확장순열(E/P)

$E/P$
4 1 2 3 2 3 4 1

☑️ Input(4-bit) :

1	0	0	1

☑️ Output(8-bit) :

1	1	0	0	0	0	1	1
4	1	2	3	2	3	4	1

④ k1(8-bit)와 XOR연산

☑️ Input(8-bit) :

1	1	0	0	0	0	1	1

☑️ k1(8-bit) :

1	1	0	0	0	1	1	0

☑️ Output(8-bit) :

Result	0	0	0	0	0	1	0	1
Input	1	1	0	0	0	1	1	0	⊕
k1	1	1	0	0	0	0	1	1

⑤ 4-bit 단위로 L블록과 R블록을 나눠 S-Box에 치환

☑️ L블록을 $S_{0}$ 치환 :

L블록(4-bit)에서 1, 4비트는 행 ⇒ 00

1	2	3	4
0	0	0	0

L블록(4-bit)에서 2, 3비트는 열 ⇒ 00

1	2	3	4
0	0	0	0

S_{0} = \begin{bmatrix} 1 & 0 & 3 & 2 \\ 3 & 2 & 1 & 0 \\ 0 & 2 & 1 & 3 \\ 3 & 1 & 3 & 2 \end{bmatrix}

⇒ 0행 0열의 '1'

0	1

R블록(4-bit)에서 1, 4비트는 행 ⇒ 01

1	2	3	4
0	1	0	1

R블록(4-bit)에서 2, 3비트는 열 ⇒ 10

1	2	3	4
0	1	0	1

S_{1} = \begin{bmatrix}0 & 1 & 2 & 3 \\ 2 & 0 & 1 & 3 \\ 3 & 0 & 1 & 0 \\ 2 & 1 & 0 & 3 \end{bmatrix}

⇒ 1행 2열의 '1'

0	1

☑️ Output(4-bit) :

0	1	0	1

⑥ 순열(P4)

P4
2 4 3 1

☑️ Input(4-bit) :

0	1	0	1

☑️ Output(4-bit) :

비트열을 P4에 적용하여 순열 변환

1	1	0	0
2	4	3	1

⑦ $L_{0}$ 블록과 XOR연산

☑️ Input(4-bit) :

1	1	0	0

☑️ $L_{0}$ (4-bit) :

1	1	1	0

☑️ Output(4-bit) :

Result	0	0	1	0
Input	1	1	0	0	⊕
$L_{0}$	1	1	1	0

⑧ 연산 출력 블록과 $R_{0}$ 블록을 스왑(SW)

☑️ Input :

0	0	1	0

☑️ Input || $R_{0}$ (8-bit):

맨 처음 $R_{0}$ 블록과 접하여 8-bit 블록 구성

input	$R_{0}$
0 0 1 0	1 0 0 1

☑️ Output(8-bit) :

양쪽 블록을 SWAP하여 비트열 재정렬

1	0	0	1	0	0	1	0

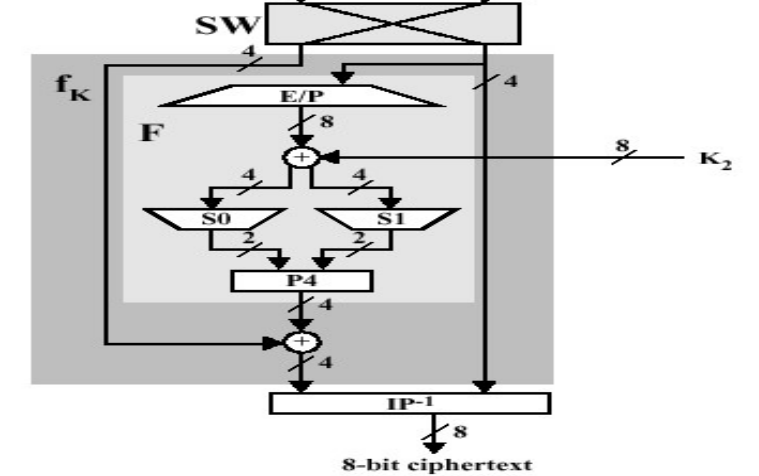
▶️ ROUND 2

Input :

1	0	0	1	0	0	1	0

k2 :

0	1	0	0	1	1	0	1

① 4-bit 단위로 $L_{1}$ 블록과 $R_{1}$ 블록으로 나눔

☑️ $L_{1}$ (4-bit) :

1	0	0	1

☑️ $R_{1}$ (4-bit) :

0	0	1	0

② $R_{1}$ 블록(4-bit) 확장순열(E/P)

$E/P$
4 1 2 3 2 3 4 1

☑️ Input(4-bit) :

0	0	1	0

☑️ Output(8-bit) :

0	0	0	1	0	1	0	0
4	1	2	3	2	3	4	1

③ k2(8-bit)와 XOR연산

☑️ Input(8-bit) :

0	0	0	1	0	1	0	0

☑️ k2(8-bit) :

0	1	0	0	1	1	0	1

☑️ Output(8-bit) :

Result	0	1	0	1	1	0	0	1
Input	0	0	0	1	0	1	0	0	⊕
k1	0	1	0	0	1	1	0	1

④ 4-bit 단위로 L블록과 R블록을 나눠 S-Box에 치환

☑️ L블록을 $S_{0}$ 치환 :

L블록(4-bit)에서 1, 4비트는 행 ⇒ 01

1	2	3	4
0	1	0	1

L블록(4-bit)에서 2, 3비트는 열 ⇒ 10

1	2	3	4
0	1	0	1

S_{0} = \begin{bmatrix} 1 & 0 & 3 & 2 \\ 3 & 2 & 1 & 0 \\ 0 & 2 & 1 & 3 \\ 3 & 1 & 3 & 2 \end{bmatrix}

⇒ 1행 2열의 '1'

0	1

R블록(4-bit)에서 1, 4비트는 행 ⇒ 11

1	2	3	4
1	0	0	1

R블록(4-bit)에서 2, 3비트는 열 ⇒ 00

1	2	3	4
1	0	0	1

S_{1} = \begin{bmatrix}0 & 1 & 2 & 3 \\ 2 & 0 & 1 & 3 \\ 3 & 0 & 1 & 0 \\ 2 & 1 & 0 & 3 \end{bmatrix}

⇒ 3행 0열의 '2'

1	0

☑️ Output(4-bit) :

0	1	1	0

⑤ 순열(P4)

P4
2 4 3 1

☑️ Input(4-bit) :

0	1	1	0

☑️ Output(4-bit) :

비트열을 P4에 적용하여 순열 변환

1	0	1	0
2	4	3	1

⑥ $L_{1}$ 블록과 XOR연산

☑️ Input(4-bit) :

1	0	1	0

☑️ $L_{1}$ (4-bit) :

1	0	0	1

☑️ Output(4-bit) :

Result	0	0	1	1
Input	1	0	1	0	⊕
$L_{1}$	1	0	0	1

⑦ $R_{1}$ 블록과 $f_{k2}$ 함수 출력 블록을 접하고 역순열( $IP^{-1}$ )

$IP^{-1}$
4 1 3 5 7 2 8 6

☑️ Input || $R_{1}$ (8-bit) :

맨 처음 $R_{1}$ 블록과 접하여 8-bit 블록 구성

input	$R_{1}$
0 0 1 1	0 0 1 0

☑️ Output(8-bit) :

1	0	1	0	1	0	0	0
4	1	3	5	7	2	8	6

Output

8-bit 암호문(Ciphertext)

1	0	1	0	1	0	0	0

박유란

doby is freeeeee

2개의 댓글

shun_1403

2024년 11월 12일

잘보고갑니다

답글 달기

장완중

2025년 3월 25일

암호학 수업들으면서 도움됐어요 감사합니다!

답글 달기

S-DES(Simplified Data Encryption Standard)

컴퓨터보안

<알고리즘>

<예제>

Input

1) Key(10-bit)값으로 (K1, K2) 생성

① 순열(P10)

②-(1) 5-bit 단위로 Shift연산(LS-1)

②-(2) 순열(P8): k1 생성

③-(1) Shift연산(LS-2)

③-(2) 순열(P8): k2 생성

2) 암호화 과정

▶️ ROUND 1

① 초기순열(IP)

② 4-bit 단위로 L0L_{0}L0​블록과 R0R_{0}R0​블록으로 나눔

③ R0R_{0}R0​블록(4-bit) 확장순열(E/P)

④ k1(8-bit)와 XOR연산

⑤ 4-bit 단위로 L블록과 R블록을 나눠 S-Box에 치환

⑥ 순열(P4)

⑦ L0L_{0}L0​블록과 XOR연산

⑧ 연산 출력 블록과 R0R_{0}R0​블록을 스왑(SW)

▶️ ROUND 2

① 4-bit 단위로 L1L_{1}L1​블록과 R1R_{1}R1​블록으로 나눔

② R1R_{1}R1​블록(4-bit) 확장순열(E/P)

③ k2(8-bit)와 XOR연산

④ 4-bit 단위로 L블록과 R블록을 나눠 S-Box에 치환

⑤ 순열(P4)

⑥ L1L_{1}L1​블록과 XOR연산

⑦ R1R_{1}R1​블록과 fk2f_{k2}fk2​함수 출력 블록을 접하고 역순열(IP−1IP^{-1}IP−1)

Output

2개의 댓글

② 4-bit 단위로 $L_{0}$ 블록과 $R_{0}$ 블록으로 나눔

③ $R_{0}$ 블록(4-bit) 확장순열(E/P)

⑦ $L_{0}$ 블록과 XOR연산

⑧ 연산 출력 블록과 $R_{0}$ 블록을 스왑(SW)

① 4-bit 단위로 $L_{1}$ 블록과 $R_{1}$ 블록으로 나눔

② $R_{1}$ 블록(4-bit) 확장순열(E/P)

⑥ $L_{1}$ 블록과 XOR연산

⑦ $R_{1}$ 블록과 $f_{k2}$ 함수 출력 블록을 접하고 역순열( $IP^{-1}$ )