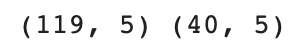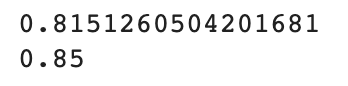❓ 문제 정의
데이터가 한번에 들어오는 것이 아니라 데이터가 조금씩 계속 추가된다!
해결 방법 1️⃣: 데이터가 들어올 때마다 훈련을 다시 시키자!
-> 데이터가 계속 늘어날텐데 저장공간도 만만치 않고 훈련 시키는데 점점 더 많은 시간이 소요될 듯!
해결 방법 2️⃣: 그러면 이전에 가지고 있던 데이터를 좀 버려서 데이터 크기를 유지시키자!
-> 버려진 데이터 중에 중요한 데이터가 포함되어 있다면 모델 성능에 영향을 미칠 듯!
해결 방법 3️⃣: 훈련시켜 둔 기존 모델을 버리지 말고 새로운 데이터만 추가로 학습 시키자!
-> 점진적 학습(Incremental Learning)/온라인 학습(Online Learning)이라고 함
📑 확률적 경사 하강법(Stochastic Gradient Descent)
확률적 경사 하강법(Stochastic Gradient Descent)은 점진적 학습 알고리즘 중에 하나로 손실(Loss)이 가장 작은 지점을 찾는 것이다.
손실(Loss)
예측 값과 실제값 간의 차이를 의미한다.
비용(Cost), 오차(Error)로도 불린다.
오차의 종류는 다음과 같다.
1️⃣ 평균 절대 오차(Mean Absolute Error, MAE)

2️⃣ 평균 제곱 오차(Mean Square Error, MSE)
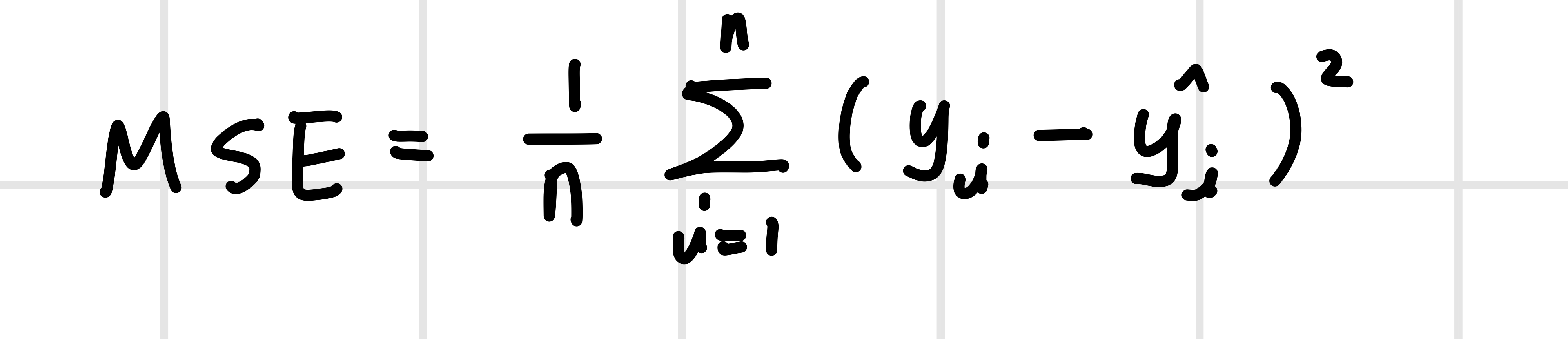
3️⃣ 평균 제곱근 오차(Root Mean Square Error, RMSE)
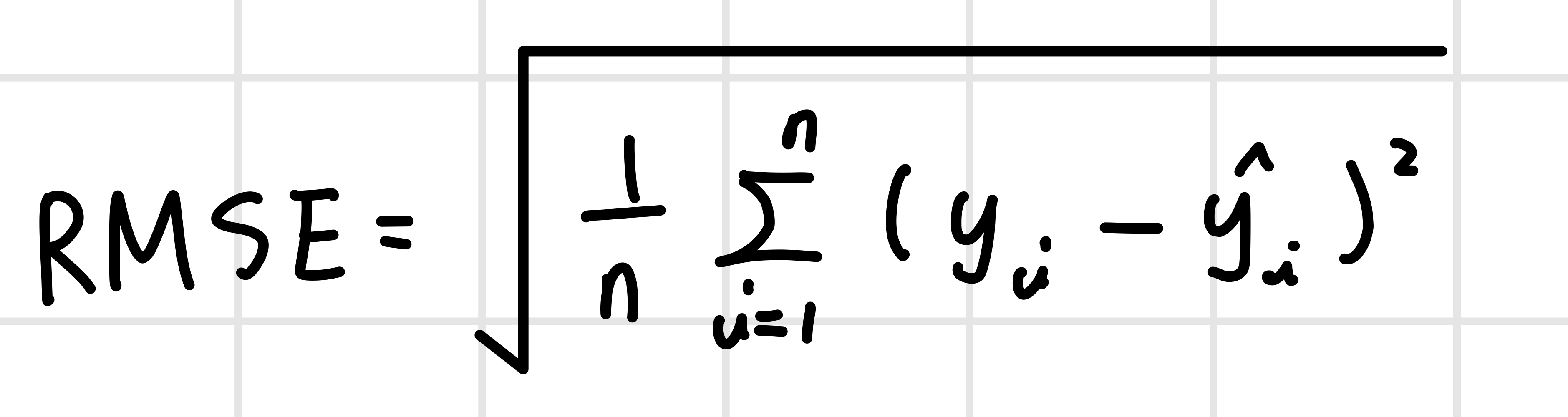
4️⃣ 이진 교차 엔트로피(Binary Cross-entropy)
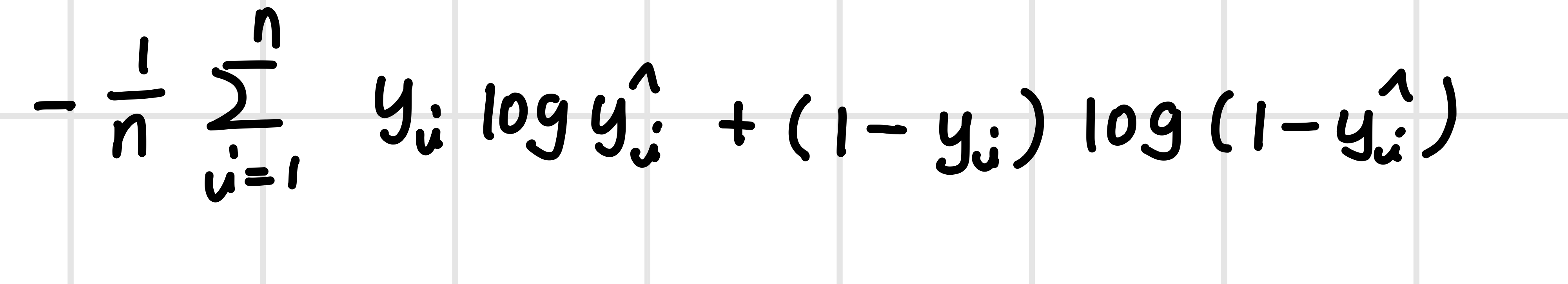
5️⃣ 카테고리컬 교차 엔트로피(Categorical Cross-entropy)
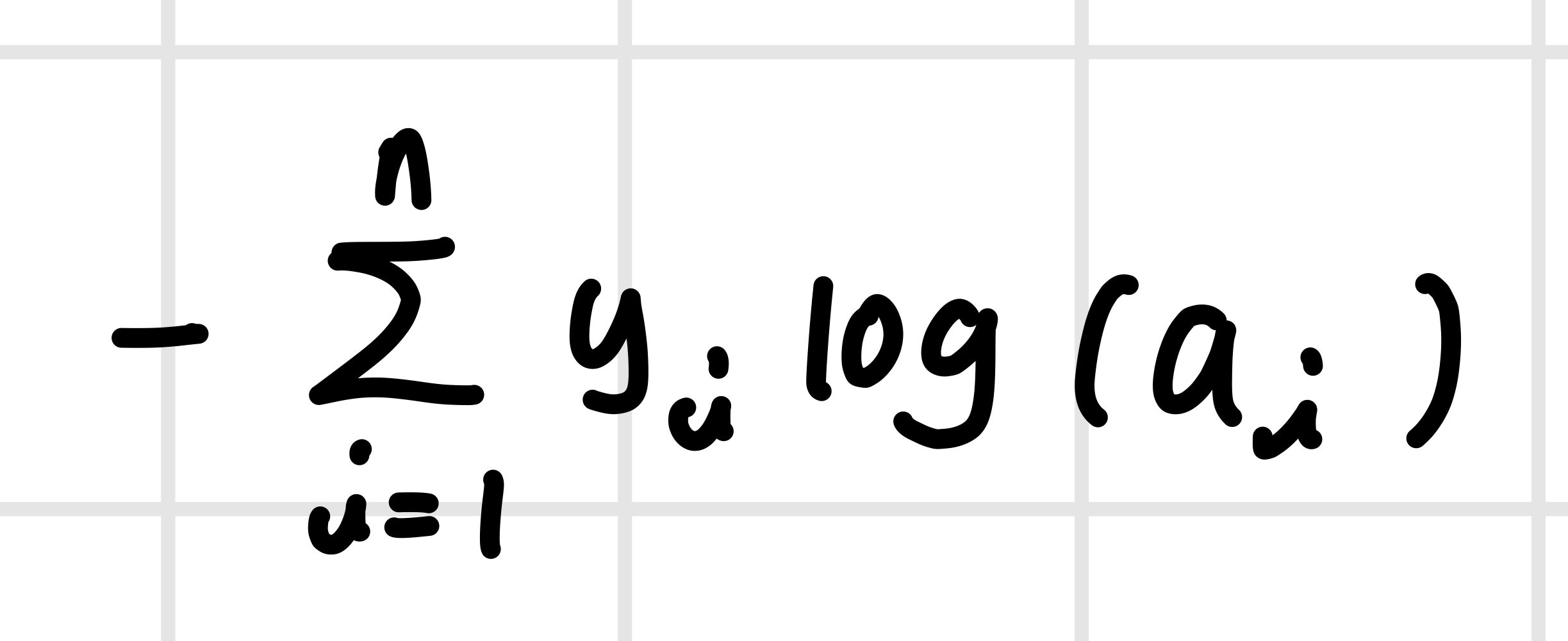
손실 함수(Loss Function)
위의 손실을 정의한 함수를 손실함수라고 한다.
손실 함수는 비용 함수(Cost Function), 오차 함수(Error Function)라고도 한다.
로지스틱 손실 함수
책에서는 여러개의 손실함수 중 로지스틱 손실함수에 대해 설명하고 있다.
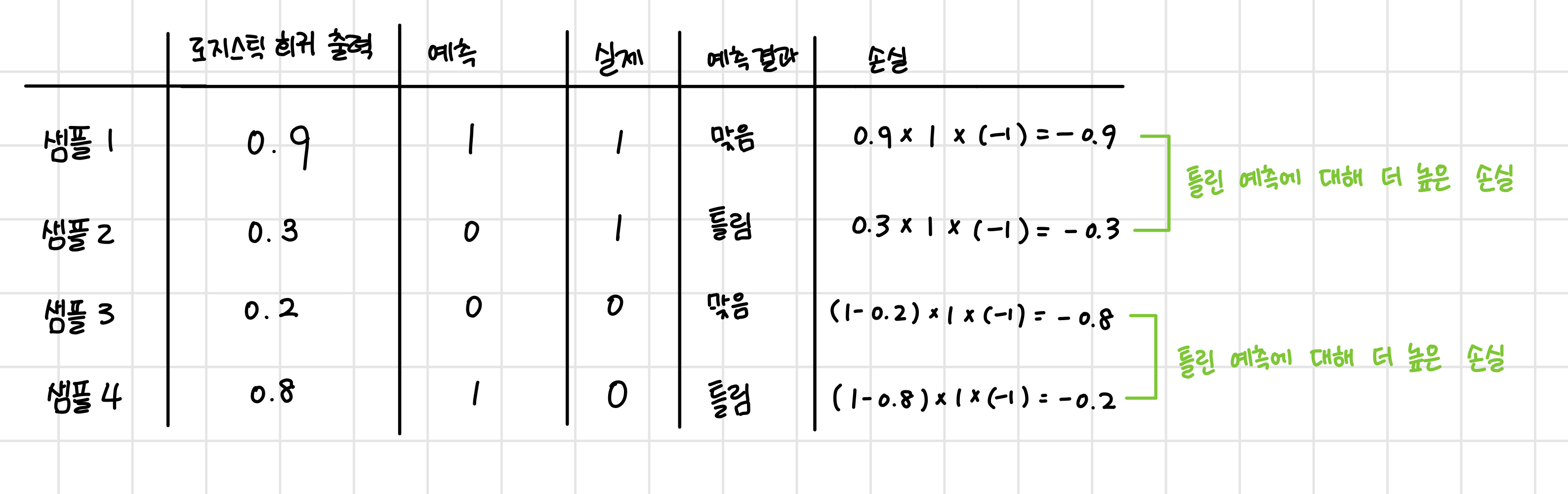
손실함수는 맞춘 예측에 대한 손실은 작게, 틀린 예측에 대한 손실은 크게 만들어 주는게 포인트다.
로지스틱 회귀에서는 출력값이 양성 클래스(1)일 확률을 출력한다.
1️⃣ 실제 샘플이 양성 클래스라면
1에 가까운 값을 내는 것이 좋은 예측이다.
그렇다면 예측값에 -1을 곱해 음수를 취해 주면 1에 가까울수록 작은 손실을 만들어줄 수 있다.
2️⃣ 실제 샘플이 음성 클래스라면
예측값이 0에 가까워져야 좋은 예측이므로 단순히 음수를 취해주는 방법은 이용할 수 없다.
따라서 1에서 예측값을 뺀 후 음수를 취해주면 작은 손실을 만들어줄 수 있다.
보통 이 값을 그대로 사용하는 것이 아니고 마이너스 로그()를 취해서 손실로 사용한다.
로그함수는 예측 확률 또는 (1-예측확률) 범위인 0~1 사이에서 매우 큰 음수값을 가지므로 함수를 취해주면 오차값을 크게 만들어줄 수 있다.
경사 하강법(Gradient Descent)
모델의 가중치(계수)를 변경하면서 손실함수가 최소인 지점을 찾자
예를 들어 다음과 같은 손실함수가 있다고 가정했을 때
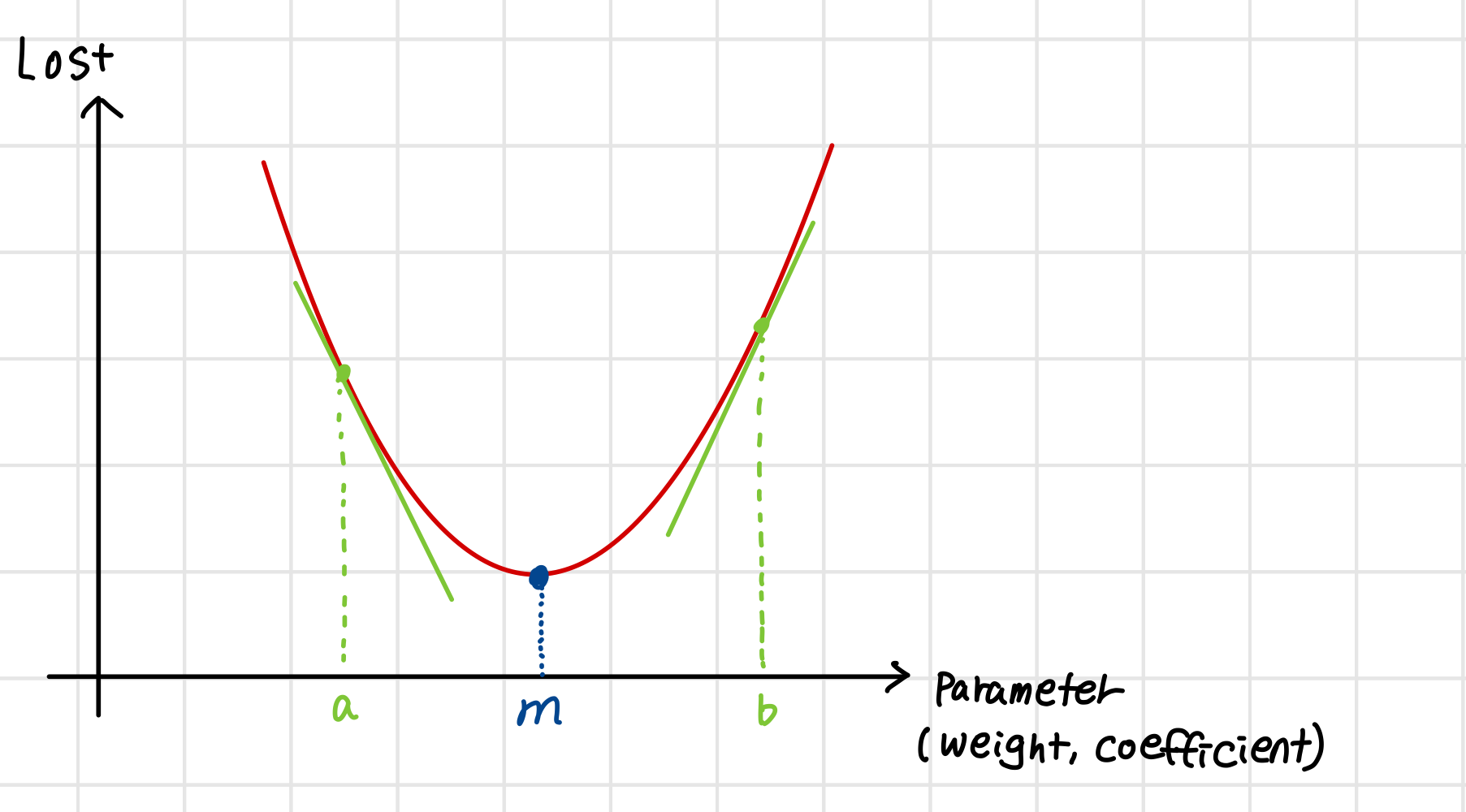
목적은 m(미분계수가 0인 지점)을 찾는 것이다!

그러면 이쯤에서 "그냥 미분 방정식을 풀어서 해를 찾으면 되는거 아니냐!"라고 할 수도 있다.
그런데 일반적으로 손실함수는 일차함수나 이차함수처럼 간단한 함수가 아니기 때문에 미분방정식을 푸는게 더 오래 걸린다!
그런데 미분계수가 0인 지점만 찾으면 되는게 아니다...!
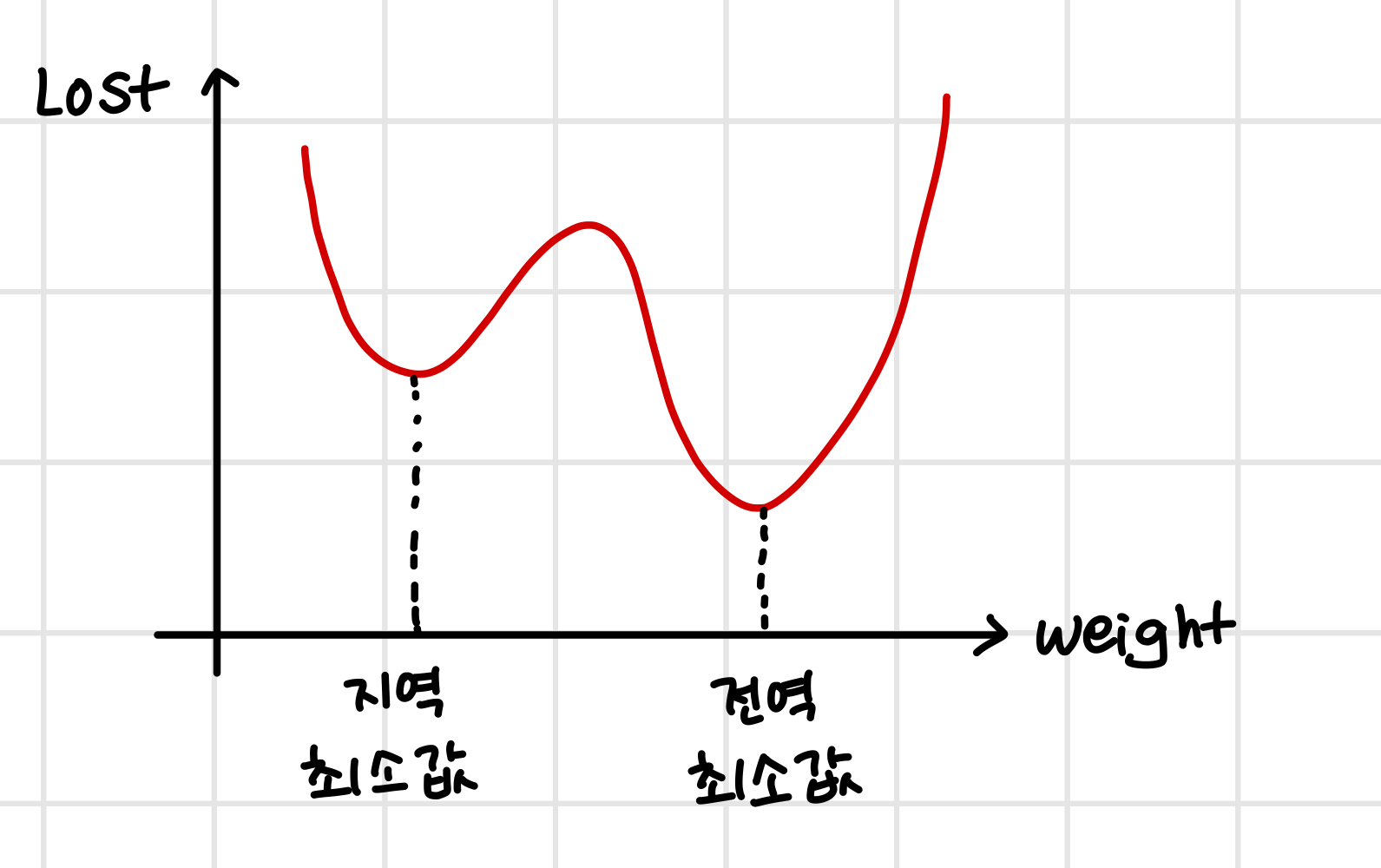
만약 손실함수가 위처럼 생겼으면 미분 계수가 0이지만 그 값이 최소가 아닐 수도 있다.
우리의 목적은 지역 최소값들 중 전역 최소값을 찾는 것이 목표이다!
그러나 전역 최소값을 찾는 것은 매우 어려운 일이기 때문에 어느정도 지역 최소값들을 찾으면 그 값들 중 최소값을 전역 최소값으로 간주한다.
배치 경사 하강법(Batch gradient descent)
파라미터가 바뀔 때마다 손실함수 변화량(그래디언트 벡터, gradient vector) 측정
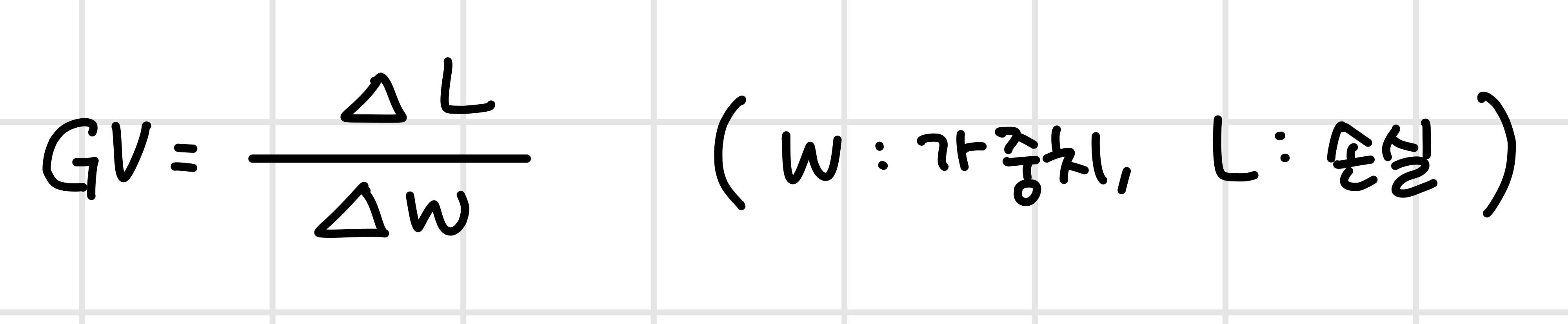
기울기가 커지면 반대방향, 작아지면 그 방향으로 이동한다.
벡터가 아주 작아지면 그 지점의 미분계수가 0인 지점으로 판단한다.
매 스텝에서 모든 데이터의 편도함수(기울기) 계산
확률적 경사 하강법(Stochastic gradient descent)
매 스텝에서 무작위로 한 개의 데이터를 선택하여 그래디언트 벡터를 계산한다.
초반 학습률을 크게 설정하고 점점 학습률을 줄여가면서 지역 최소값을 피하면서 전역 최소값을 찾도록 학습률을 조정하기도 한다.(learning rate annealing)
⭐️ 미니 배치 경사 하강법(Mini-batch gradient descent)
배치 경사 하강법과 확률적 경사 하강법의 장점만 이용하는 방법이다.
전체 훈련 세트를 등분한 미니배치에 대해 그래디언트 벡터를 계산한다.
보통 배치 사이즈는 8로 지정하는데, 이는 한개의 미니 배치에서 8개의 그래디언트 벡터를 계산하는 것을 말한다.
💽 데이터 준비
import pandas as pd
fish = pd.read_csv('https://bit.ly/fish_csv_data')
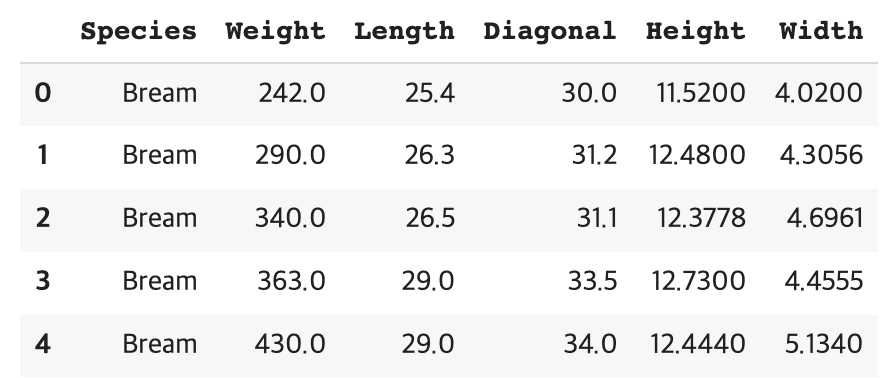
fish.head(5)# input, target 데이터 나누기
fish_input = fish[['Weight', 'Length', 'Diagonal', 'Height', 'Width']].to_numpy()
fish_target = fish['Species'].to_numpy()
print(fish_input[:5], fish_target[:5])# train set, test set 나누기
from sklearn.model_selection import train_test_split
train_input, test_input, train_target, test_target = train_test_split(fish_input, fish_target, random_state=42)
print(train_input.shape, test_input.shape)# 표준화 전처리
from sklearn.preprocessing import StandardScaler
ss = StandardScaler()
ss.fit(train_input)
train_scaled = ss.transform(train_input)
test_scaled = ss.transform(test_input)
print(train_scaled[:5])🤖 모델 학습: SGDClassifier
지금 예제에서는 확률적 경사 하강법을 이용하여 가장 최적화된 모델을 만들 예정이다.
사이킷런에서 확률적 경사 하강법을 제공하는 모델은 SGDClassifier이다.
SGDClassifier는 sklearn의 linear_model 아래에 있다.
객체에 loss 매개변수로 손실함수의 종류를 지정할 수 있다. 여기서는 위에서 설명한 로지스틱 손실 함수를 사용하기 위해 'log'로 지정했다.
max_iter는 에포크 횟수를 지정하는 매개변수이다. 우선 10으로 지정했다.
from sklearn.linear_model import SGDClassifier
sc = SGDClassifier(loss='log', max_iter=10, random_state=42)
sc.fit(train_scaled, train_target)
print(sc.score(train_scaled, train_target))
print(sc.score(test_scaled, test_target))
- 데이터는 다중 클래스였지먄 로지스틱 손실 함수를 사용하면서 도미만을 양성 클래스로 간주하고 나머지 클래스는 음성 클래스로 간주하게 되었다.
- ConvergenceWarning은 모델이 충분하게 수렴하지 않았다는 경고로 즉 에포크 횟수가 부족함을 의미한다.
해결 방법은 max_iter 값을 충분히 늘려 주면 된다.
partial_fit(): 모델을 이어서 추가로 훈련시킬 때
점진적인 학습을 시킬 때에는 새로운 모델을 만들어 주는 것이 아닌 기존 모델에 partial_fit() 메서드를 이용하여 추가로 훈련을 시켜준다.
한 번 호출할 때마다 1 에포크씩 추가로 훈련을 수행한다.
sc.partial_fit(train_scaled, train_target) # 11에포크
print(sc.score(train_scaled, train_target))
print(sc.score(test_scaled, test_target))
이전에 10 에포크를 훈련 시켰던 점수에 비해 훈련 세트와 테스트 세트 모두 점수가 올랐다.
적절한 에포크 수로 훈련하여 과소적합, 과대적합 피하기
너무 적은 에포크 수로 학습을 하게 되면 모델이 훈련 세트를 다 학습하기 전에 훈련이 끝나므로 과소적합 될 확률이 크다.
반대로 너무 큰 에포크 수로 학습을 하게 되면 모델이 훈련 세트를 너무 학습하여 과대적합될 가능성이 커진다.
따라서 에포크 수가 충분히 크되 과대적합 되기 전에 훈련을 멈춰주어야 하는데, 이를 조기종료(early stopping)라고 한다.
for 루프를 이용하여 적절한 에포크 수를 찾아야 한다.
따라서 아래 예제에서는 partial_fit() 메소드만 사용하여 에포크 수에 따른 훈련 세트와 테스트 세트의 정확도 변화를 살펴보도록 하자.
partial_fit() 메소드만 사용하려면 target에 어떤 클래스가 있는지 전달해 주어야 한다.
# 에포크 수에 따른 점수 기록
import numpy as np
sc = SGDClassifier(loss='log', random_state=42)
train_score = []
test_score = []
classes = np.unique(train_target)np.unique() 메서드를 통해 생선 목록 리스트를 만들어서 전달해 주려고 한다.
for _ in range(0, 300):
sc.partial_fit(train_scaled, train_target, classes=classes)
train_score.append(sc.score(train_scaled, train_target))
test_score.append(sc.score(test_scaled, test_target))1 에포크마다 점수를 train_score, test_score 리스트에 기록해 주었다.
import matplotlib.pyplot as plt
plt.plot(train_score)
plt.plot(test_score)
plt.xlabel('epoch')
plt.ylabel('accuracy')
plt.show()
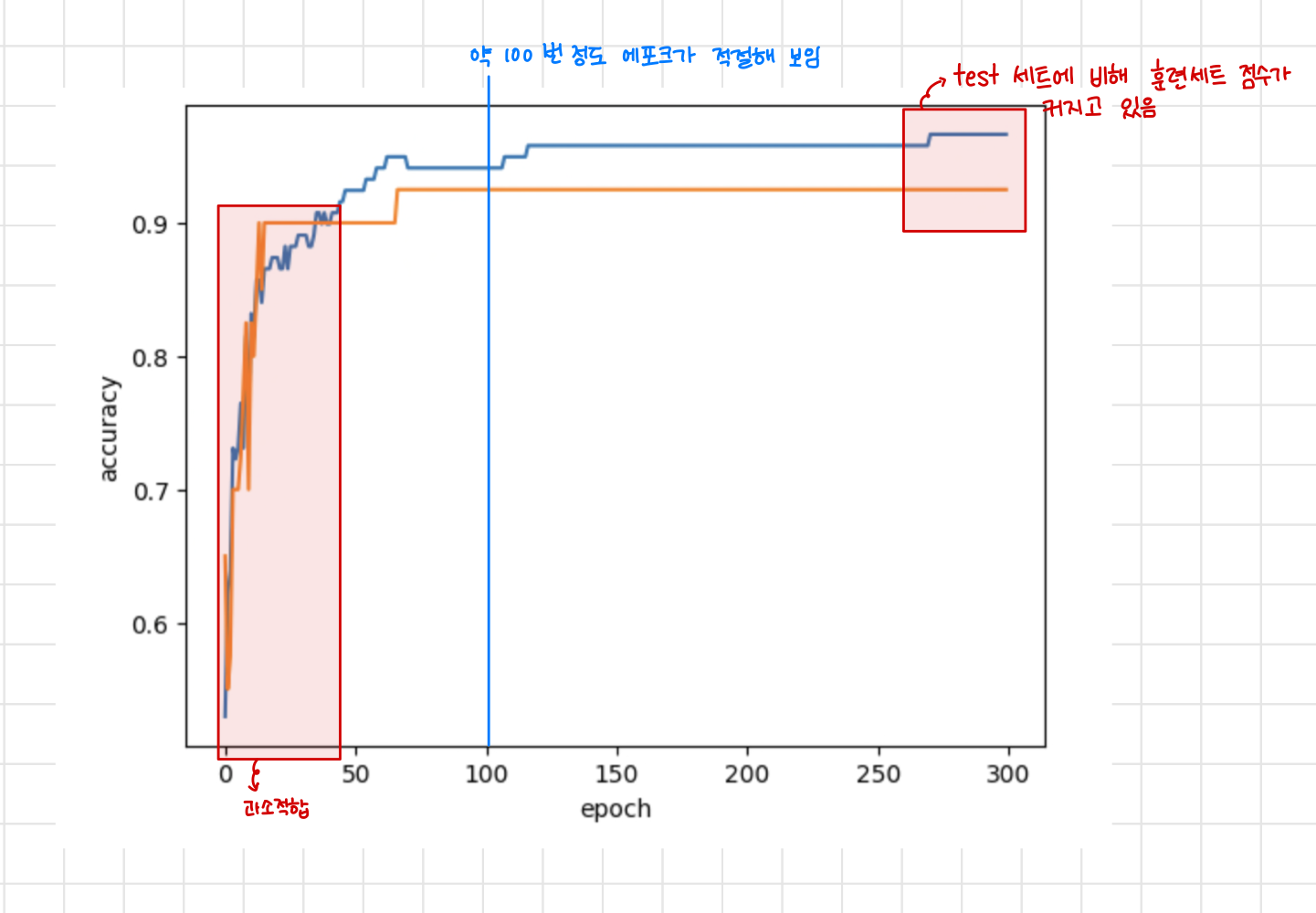
파란색 그래프가 훈련 세트 점수이고 주황색이 테스트 세트 점수이다.
너무 적은 에포크 수라면 훈련 세트, 테스트 세트 모두 정확성이 낮은 과소적합이다.
테스트세트 점수는 어느 순간 거의 증가하지 않는데, 훈련세트는 계속해서 조금씩 증가하여 어느 시점이 지나면 그 차이가 커지는 것을 확인할 수 있다.(과대적합 경향)
약 100 에포크 정도라면 테스트세트 점수도 충분히 높고 과대 적합 경향도 일어나지 않는 적절한 수준으로 볼 수 있다.
적절한 에포크 수를 찾았으니 max_iter 매개변수를 바꿔서 모델을 다시 만들어보자.
SGDClassifier는 n 에포크 동안 성능이 향상되지 않으면 조기종료 시키는데, tol 매개변수로 향상될 최솟값을 지정한다.
아래 코드에서는 None으로 지정하여 조기종료가 없도록 한다.
sc = SGDClassifier(loss='log', max_iter=100, tol=None, random_state=42)
sc.fit(train_scaled, train_target)
print(sc.score(train_scaled, train_target))
print(sc.score(test_scaled, test_target))
모델이 과소적합이나 과대적합 되지 않고 훈련세트와 테스트 세트에서 점수가 잘 나온 것을 확인할 수 있다.
로지스틱 손실 함수 말고 다른 손실함수를 사용하여 손실을 다른 방식으로 계산할 수 있다.
위에서 설명한 것처럼 loss 매개변수를 바꿔주면 되는데 SGDClassifier의 loss 매개변수 기본값은 힌지 손실(hinge loss)이다.
힌지 손실은 서포트 벡터 머신(support vector machine, SVM)에서 주로 사용하는 손실함수이다.
sc = SGDClassifier(loss='hinge', max_iter=100, tol=None, random_state=42)
sc.fit(train_scaled, train_target)
print(sc.score(train_scaled, train_target))
print(sc.score(test_scaled, test_target))
📚 Reference
혼자 공부하는 머신러닝+딥러닝, 박해선, 한빛미디어