[알고리즘] 소수 찾기 - JS

문제 바로가기

문제 설명

1부터 입력받은 숫자 n 사이에 있는 소수의 개수를 반환하는 함수, solution을 만들어 보세요.

소수는 1과 자기 자신으로만 나누어지는 수를 의미합니다.
(1은 소수가 아닙니다.)

제한 조건

n은 2이상 1000000이하의 자연수입니다.

입출력 예

n result
10 4
5 3

입출력 예 설명

입출력 예 #1
1부터 10 사이의 소수는 [2,3,5,7] 4개가 존재하므로 4를 반환

입출력 예 #2
1부터 5 사이의 소수는 [2,3,5] 3개가 존재하므로 3를 반환

Solution

처음 코드

function isPrime(num) {
    if(num==1) return false
    for (let i = 2; i <= parseInt(Math.sqrt(num)); i++) {
        if (num % i === 0) {
            return false
        }
       }
    return true
}

function solution(n) {
    let answer=0;
    for (let i = 1 ; i <= n; i++) {
      if (isPrime(i)) {
        answer++
    }
}
    return answer
}

처음에는 isPrime 소수판별하는 함수를 만들어 판별을 했다.
테스트 케이스는 통과했지만, 효율성에서 통과되지 못했다.

해결방법 ) '에라토스테네스의 체'라는 알고리즘이 있었고 이를 이용해서 효율성을 통과시켰다.

'에라토스테네스의 체'

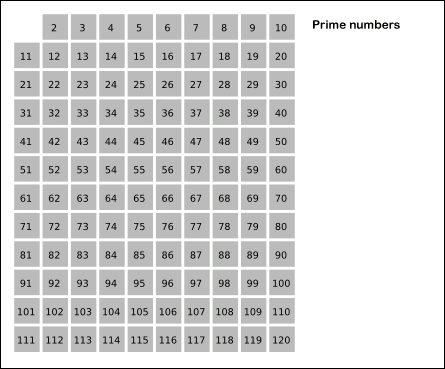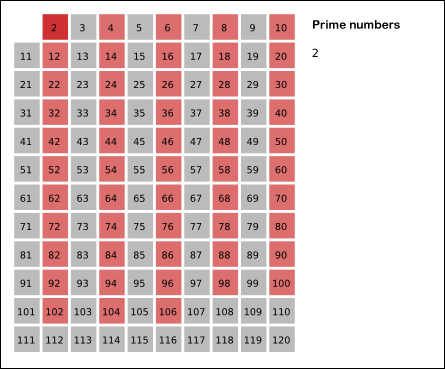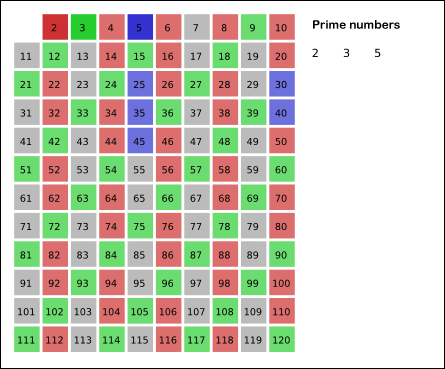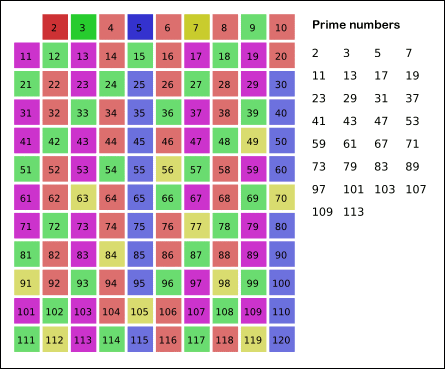
1을 제외하고 2부터 순차적으로 N까지 자신을 제외하고 자신의 배수들을 차례대로 지워가면 결국에는 소수들만 남는다는 원리이다.
여기서 N까지가 아니라 √N까지만 검사해도 결과는 같다.

에라토스테네스 체는 먼저 소수를 먼저 판별할 범위만큼 배열할당에 그 인덱스에 해당하는 값을 넣어준다.

function solution(n) {
    let count=0;
    let ch=Array.from({length:n}, ()=>1); //배열 값들을 모두 1로 만들어줌
    for (let i = 2 ; i <= n; i++){
        if(ch[i]!==0){
          //값이 0이 아닐경우 count++
            count++;
            for(let j=i; j<=n; j+=i){
              //배수들을 0으로 만들어줌
                ch[j]=0;
            }
        }
    }
    return count;
}

let PrimeArray = [];

function Eratos(n){
    if(n<=1) return;

    for(let i=2; i<=n; i++){
        PrimeArray[i] = true
    }

    for(let i=2; i*i <=n; i++){
        if(PrimeArray[i])
            for(let j=i*i; j<=n; j+=i)
                PrimeArray[j] = false;
    }
}

function solution(n) {
    var answer = 0;
    Eratos(n)
    for(let i=2; i<=n+1; i++){
        if(PrimeArray[i] == true){
            answer++
        }
    }
    
    return answer;
}