✔️ 16400 소수 화폐

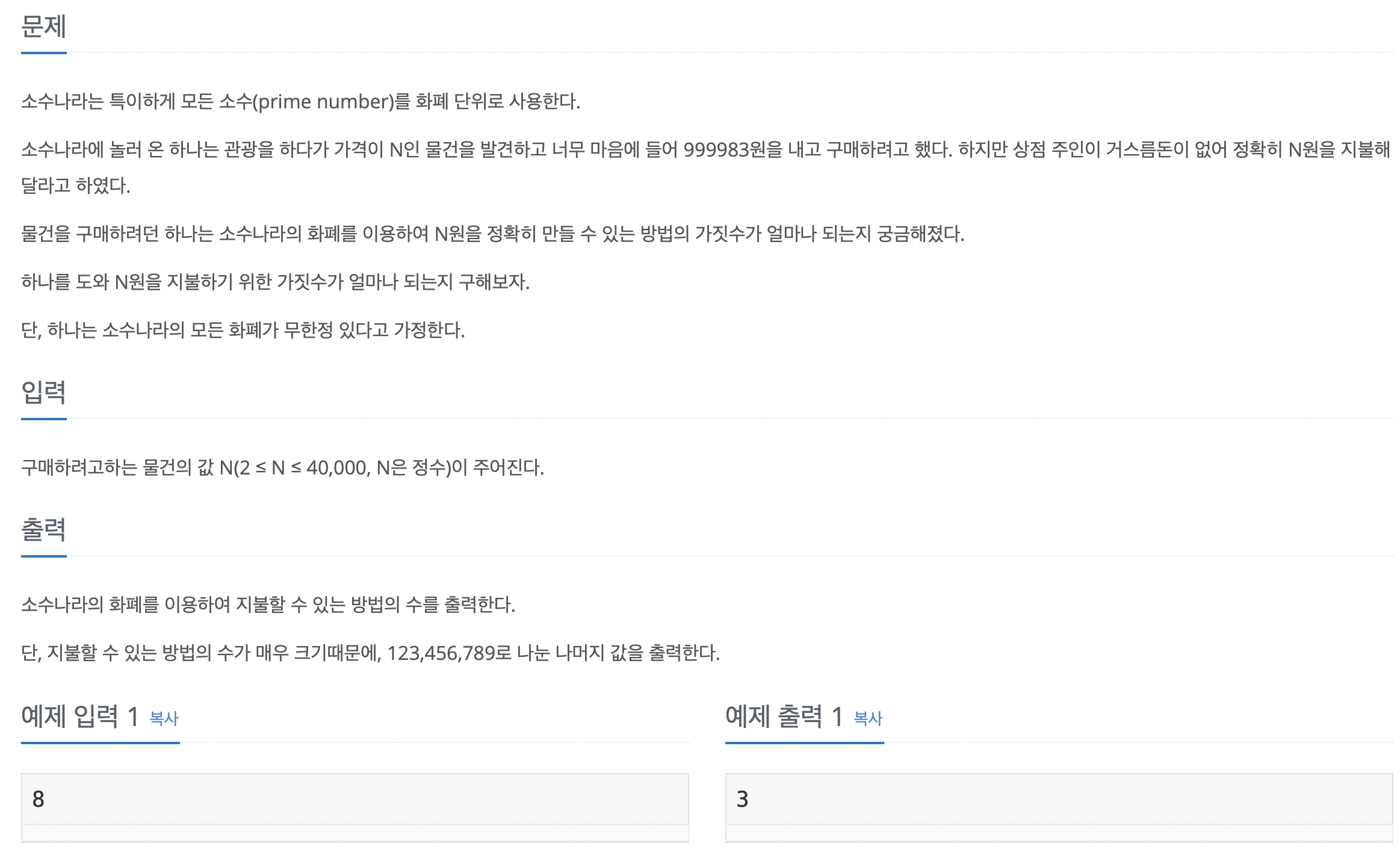
이 문제를 풀기 위해서는 에라토스테네스의 체 개념이 필요하다.

링크를 통해 내용을 참고하면 좋을 것 같다.

에라토스테네스의 체를 이용해 소수를 판별해 낸 뒤 DP로 2293번 문제처럼 풀어내면 된다.

그럼 2293 문제를 먼저 풀어보자.

---

✔️ 2293 동전 1

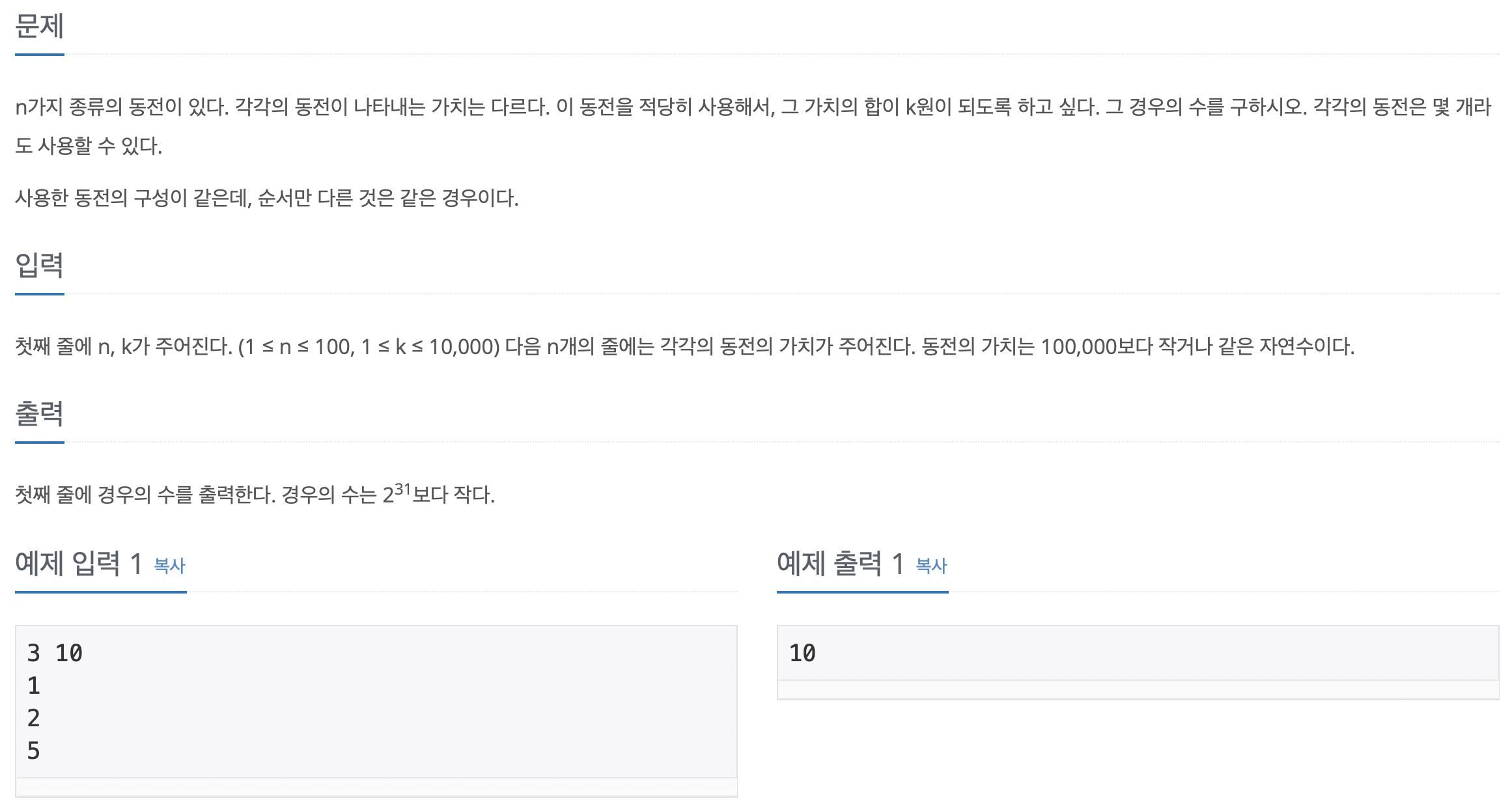
이 문제는 DP의 문제이다.

왜 DP의 문제일까?

우선 1원을 만드는 방법은 몇 가지일까?
1원은 1원으로 만드는 방법 뿐이니 1가지이다.

그럼 2원을 만드는 방법은?
1원 + 1원 = 2원
또는 2원으로 2원을 만드는 방법. 이렇게 2가지가 존재한다.

그럼 3원을 만드는 방법은?
1 + 1 + 1 = 3
1 + 2 = 3
3 = 3
이렇게 3가지이다.

3원을 만드는 방법을 보면 3가지가 1원짜리로만 + (1원 + 2원) + 3원 짜리로만 이렇게 구성이 되어있다.

즉, DP라는 배열이 DP[a] = b일 때 a를 만들 수 있는 방법 b가지라고 이해한다면,
1원 짜리로 3원을 만들 때 DP[3] += DP[2]이 된다.

왜냐하면 1원을 이용해 3원을 맞추려면 기존에 2원이 있어야 하는데 2원을 만드는 방법은 DP[2] 에 저장되어 있기 때문이다.

이 말은 즉 현재 X원 동전을 가지고 있으며 Y원을 만들 때 DP[Y] = DP[Y] + DP[Y-X] 가 된다.

📌 그런데 여기서 X원 짜리 동전으로 X원보다 작은 Y원을 절대 만들 수 없다는 것을 주의하자 (그래서 반복문이 k까지 도는 것)

#include <iostream>
using namespace std;

// 동전 1

int main() {
    ios::sync_with_stdio(0);

    int DP[100001] = {0, };      // 들어올 수 있는 동전의 가치 범위만큼

    int arr[101] = {0, };
    int n, k;
    cin >> n >> k;

    for(int i=1; i<=n; i++) {    // 동전의 가치
        cin >> arr[i];
    }

    DP[0] = 1;
    
    for(int i=1; i<=n; i++) {
        for(int j=arr[i]; j<=k; j++) {
            DP[j] += DP[j-arr[i]];
        }
    }

    cout << DP[k] << '\n';

    return 0;
}

---

↪️ 다시 16400 소수 화폐

#include <iostream>
#include <cmath>
#include <vector>
using namespace std;

// 소수 화폐

int N;                  // 물건의 값
vector<int> pNumber;    // N까지 수 중 소수만 저장

void primeNumber(int num) {
    int number[40001];

    for(int i=2; i<=num; i++) {
        number[i] = i;
    }
    
    for(int i=2; i<=num; i++) {
        if(number[i] == 0) { continue; }
        
        for(int j=i+i; j<=num; j+=i) {  // 자기 자신을 제외하고 삭제
            number[j] = 0;
        }
    }

    for(int i=2; i<=num; i++) {
        if(number[i] != 0) { pNumber.push_back(number[i]); }
    }
}

int main() {
    ios::sync_with_stdio(0);


    int sum = 0;
    int DP[40001] = {0, };

    cin >> N;

    primeNumber(N);

    DP[0] = 1;

    for(int i=0; i<pNumber.size(); i++) {
        for(int j=pNumber[i]; j<=N; j++) {
            DP[j] = (DP[j] + DP[j - pNumber[i]]) % 123456789;
            DP[j] %= 123456789;
        }
    }


    cout << DP[N] << '\n';

    return 0;
}

에라토스테네스의 체를 이해하고, 동전 1 문제를 풀고 푼다면 그 알고리즘을 이용해 쉽게 풀어낼 수 있다.

---

참고 2