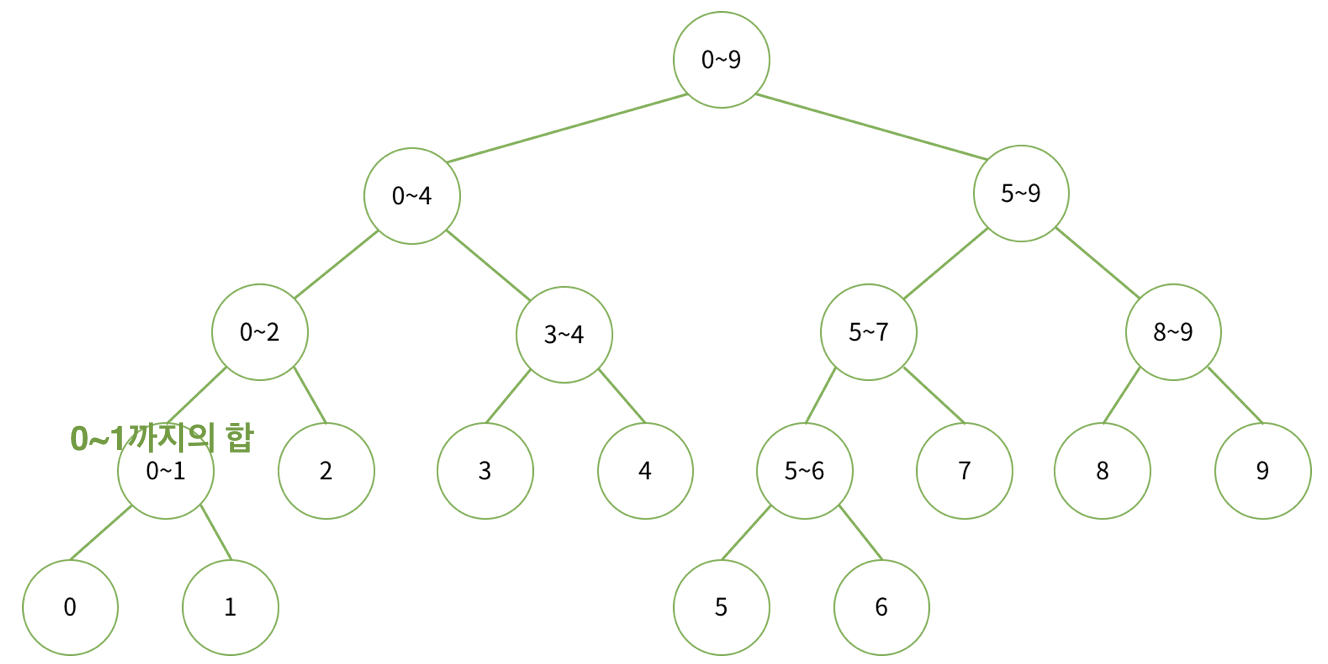
세그먼트 트리 Segment Tree
: 구간을 저장하기 위한 이진트리
또한, 데이터의 합을 가장 빠르고 간단히 구현할 수 있다.
주어진 전체에서 특정 구간에 대한 연산을 구해야 하는 경우, 가장 처음 모든 합을 구해놓고 계산하는 방식이 있을 수 있다.
그런데 이때, 값들 중 중간에 한 원소를 다른 값으로 바뀌었다면 다시 계산을 모두 해내야하기 때문에 굉장히 복잡한 계산이 된다. (배열에 한 5개씩만 있다고 가정하면 물론 어렵지 않다.)
세그먼트 트리 알아보기
우선 세그먼트 트리의 형태는 리프노드는 배열의 값 그 자체를 가지며, 나머지 노드에는 해당 자식들의 합이 저장되어 있다고 생각하자.
(참고로 리프노드는 말단 노드를 뜻한다.)
- 리프 노드: 배열의 값 그 자체
- 리프 노드를 제외한 모든 노드: 왼쪽 자식과 오른쪽 자식의 최솟값 또는 합
이렇게 되면 루트(최상단 노드)는 모든 구간의 합을 가지게 된다.
⚠️ 아 그리고 트리는 배열이든 벡터든 index 0은 버린다. 부모-자식 관계를 계산하는데 있어 복잡해지기 때문에 1부터 사용한다.
트리를 만들기 위해 트리의 크기를 알아보자.
트리의 높이는
log2(n)이다. 더 정확히는ceil(log2(n))이다.
ceil()는 무조건 올림을 수행해주어야 한다는 뜻이다.세그먼트 트리의 크기는
1<<(트리 높이+1)이다. 즉,2^(트리 높이+1)과 동일하다.
세그먼트 트리 생성하기
와 설명하기 너무 어려워요. 좀 더 공부하고 내용을 추가하도록 하겠습니다,,🥲
세그먼트 트리는 완전 이진 트리에 가까워 배열의 모든 값이 대부분 채워지게 된다.
따라서 동적 할당이 아닌 배열로 만드는 것이 유리하다.
배열에서 어떤 노드의 인덱스가 x일 때, 왼쪽 자식의 인덱스는 2*x, 오른쪽 자식의 인덱스는 (2*x)+1이 된다.
트리 배열의 크기
배열 원소의 개수를 N이라고 했을 때, N이 2의 제곱꼴인 경우에는 완전 이진 트리가 되므로 필요한 노드의 개수는 2*N-1이다.
N이 2의 제곱꼴이 아닌 경우에는 세그먼트 트리의 높이는 log2(N)이 된다.
그리고 필요한 배열의 크기는 (2^(H+1))-1이다.
이렇게 계산까지 하고싶지 않다면 그냥 N*4를 해도된다. 하지만 메모리 낭비가 발생한다.
세그먼트 트리 초기화 시간 복잡도
: O(N)
초기화할 때 각 노드마다 걸리는 시간이 O(1)이므로 노드의 개수만큼인 O(N)이 소요된다.
세그먼트 트리를 통한 합 구하기
세그먼트 트리는 top-down 방식으로 탐색한다.
만약 3~9까지의 합을 구한다면 색이 칠해져 있는 노드의 두 수만 더하면 된다.
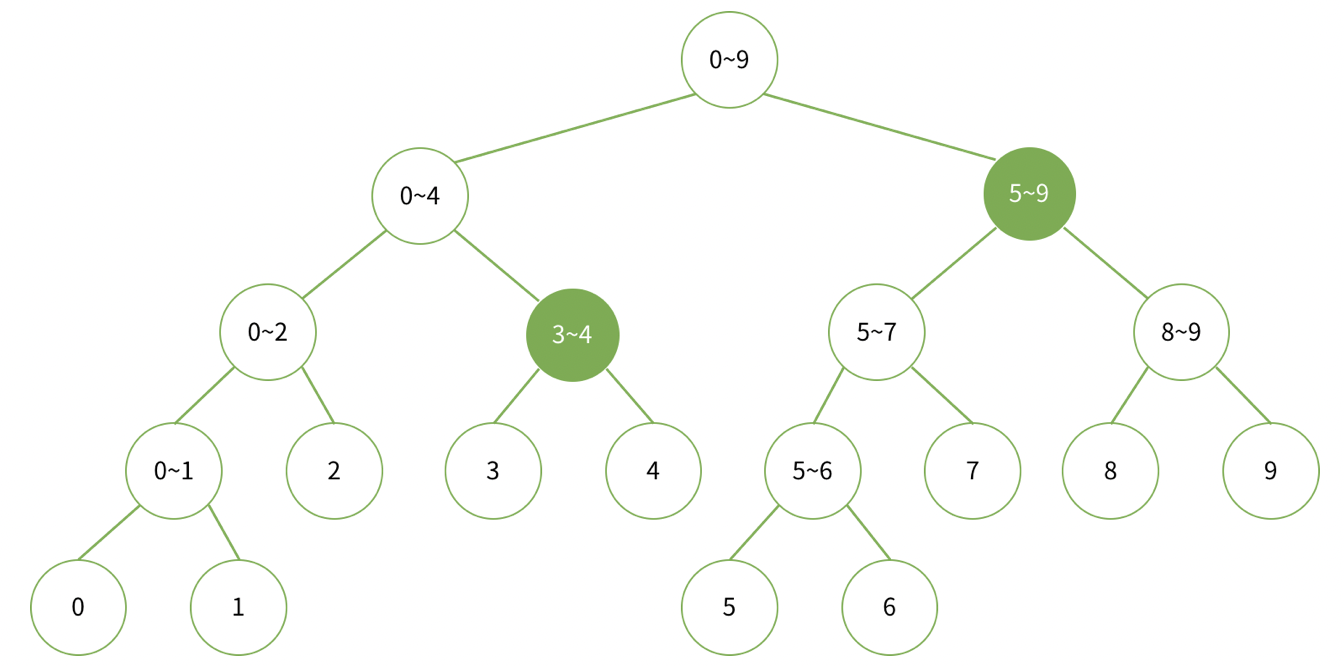🔗사진 출처
노드가 담당하는 구간이 [start, end]일 때, 합을 구해야 하는 구간이 [left, right]라고 한다면
1. [left, right]와 [start, end]가 겹치지 않는 경우: 교집합이 공집합
2. [left, right]가 [start, end]를 완전히 포함하는 경우: 교집합이 [start, end
3. [left, right]가 [start, end]를 완전히 포함하는 경우: 교집합이 [left, right]인 경우
4. [left, right]가 [start, end]가 겹쳐진 경우 (1, 2, 3번의 경우를 제외한 나머지 경우)
세그먼트 트리 탐색 시간 복잡도
: O(logN)
트리의 바닥까지 최대 두 번 탐색
세그먼트 트리 업데이트
트리의 한 노드를 변경하기 위해서는 그 숫자가 포함된 구간을 담당하는 모든 노드의 값을 함께 변경해주어야 한다.
값 갱신 과정은 초기화 과정 + 합을 구하는 과정 처럼 구현된다.
변경해야 하는 노드의 인덱스를 idx, 변경할 값을 val이라고 했을 때,
우선 그 수의 변화량(diff라고 할 때)을 알아야 한다.
diff = val - array[idx]
수 변경은 두 가지 경우가 있다.
1. [start, end]에 idx가 포함되는 경우
2. [start, end]에 idx가 포함되지 않는 경우
노드의 구간에 포함되는 1의 경우 diff 만큼 증가시켜 합을 변경해줄 수 있지만,
포함되지 않는 2의 경우 탐색을 중단하면 된다.
세그먼트 트리 업데이트 시간 복잡도
: O(logN)
원래 배열의 idx 위치를 포함하는 구간은 트리에서 logN개 있을 것이므로 (그것만 수정해주면 되므로)
특강 시간 잘 이해되지 않았던 내용 찾아보기 🙁
