슬라이딩 윈도우

• 구간의 길이가 고정된 부분 배열을 활용해 특정 조건을 일치시키는 값을 찾아내는 알고리즘

• 기준이 되는 포인터를 이동시킨다는 점에서 투포인터와 유사하지만, 길이가 고정되어 있으므로 포인터가 2개일 필요가 없다. 반면 투포인터는 부분 배열의 길이가 가변적이기 때문에 구간을 정할 포인터가 2개 있어야 한다.

대표 문제

정수로 이루어진 배열과 자연수 n이 주어졌을 때, 연속된 n개의 정수를 더한 최대값을 리턴하는 함수 maxSubarraySum을 작성하라. (빈 배열일 경우 null을 리턴한다.)

🤔 naive solution

• 내가 직접 풀어본 naive한 해결 방법은 아래와 같다. 즉 array.slice() 메서드를 사용해 n개 만큼의 요소를 갖는 배열을 복사해 요소들을 더하고, max와 비교하여 최대값을 할당하는 방법을 생각했다.

하지만 for문에서 O(N)인 메서드들을 사용하고 있으므로 최악의 경우 O(N^2)의 시간 복잡도를 갖는다.

function maxSubarraySum(arr, n) {
  let max = Number.MIN_SAFE_INTEGER;
  let sum = 0;

  if (!arr.length) return null;

  for (let i = 0; i < arr.length; i++) {
    let subArr = arr.slice(i, i + n);
    sum = subArr.reduce((acc, cur) => acc + cur, 0);
    if (sum > max) max = sum;
  }
  return max;
}

예를 들어 n이 2일 때, arr.slice(1, 1 + 2)은 arr[1], arr[2]를 요소로 갖는 새로운 배열을 복사한다. 즉 slice()메서드를 사용해 n개의 요소를 갖는 배열을 만들고 싶으면 slice(startIndex, endIndex) 에서 startIndex와 endIndex의 차가 n이 되면 된다.((i + n) - i = n 이므로)

😎 good solution

• 슬라이딩 윈도우 알고리즘은 이전 구간의 양쪽 끝에 요소를 제거하고 추가함으로써 다음 구간을 구한다.

• 즉 한 칸 이동할 때 겹치는 부분은 유지 / 구간의 가장 왼쪽 요소는 제거 / 가장 오른쪽에 요소를 추가함으로써 다음 구간을 정한다.

• 이를 그림으로 표현하면 아래와 같다.

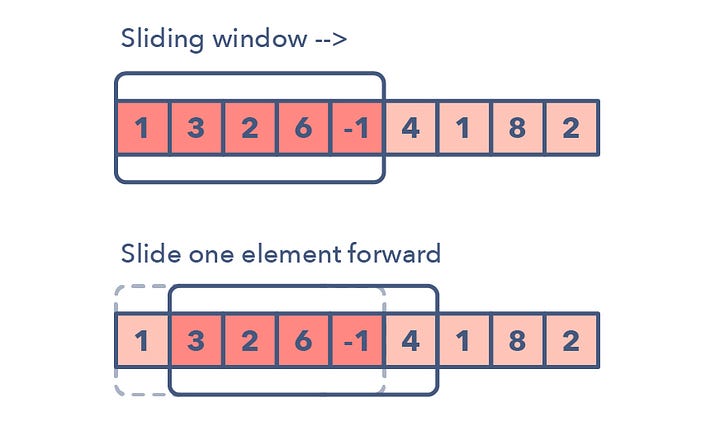
• 슬라이딩 윈도우를 활용해 구간의 합의 최대값을 구하는 코드를 다시 작성하면 아래와 같다.

function maxSubarraySum(arr, n) {
  let maxSum = 0;
  let tempSum = 0;

  if (arr.length < n) return null;

  // 맨 처음 n개를 더한 값을 mxSum에 할당한다. -> 첫 번째 구간
  for (let i = 0; i < n; i++) {
    maxSum += arr[i];
  }
  // maxSum과 동일하게 할당해준다.
  // 왜? 첫 번째 구간을 기준으로 다음 구간의 합을 구할 것이기 때문에!
  tempSum = maxSum;

  // i가 포인터가 된다. i를 기준으로 첫 번째 구간의 양쪽 끝을 구한다.
  for (let i = n; i < arr.length; i++) {
    // arr[i - n]: 이전 구간의 가장 왼쪽 요소
    // arr[i]: 가장 오른쪽에 추가될 요소
    tempSum = tempSum - arr[i - n] + arr[i];
    // 다음 구간의 합과 최대값을 비교해 저장한다.
    maxSum = Math.max(maxSum, tempSum);
  }
  return maxSum;
}

정리하자면, 특히 위 문제와 같이 구간의 합을 구하는 문제에서 슬라이딩 윈도우를 사용하기 위해서는 다음 구간의 합을 구하기 위해 이전 구간을 저장(tempSum)하고, 이전 구간의 왼쪽(arr[i - n])에는 요소 제거, 오른쪽(arr[i])에는 다음 요소 추가 하는 로직이 필요하다.

정리

• 슬라이딩 윈도우는 연속된 특정 구간의 최대값을 구하는 데 유용한 알고리즘이다.

• 투포인터와 유사하지만, 구간이 일정하므로 2개의 포인터가 필요하지 않다.

• 이전 구간의 왼쪽에 있는 요소는 제거, 오른쪽에는 요소를 추가하는 방식으로 구현한다.

• 매번 배열 요소의 합을 구하기 위한 메서드를 사용하지 않아도 되므로 시간 복잡도를 O(N)으로 줄일 수 있다.

참고 자료

【한글자막】 JavaScript 알고리즘 & 자료구조 마스터클래스

이미지 출처 - Sliding Window Algorithm