MM algorithm

MM algorithm은 EM algorithm의 일반화된 버전으로 이해하면 되는데, MM은 maximization 관점에서 minorize-maximize를 나타낸다. MM algorithm은 최대화하고자 하는 목적함수 $l(\theta)$ 에 대한 lower bound function(surrogate function) $Q(\theta,\theta^{t})$ 를 찾고 이를 maximize하는 $\theta^{t+1}$을 찾아 updating하는 방식으로 이루어진다. 이 메커니즘은 다음과 같은 monotonic increasing property를 보장한다.

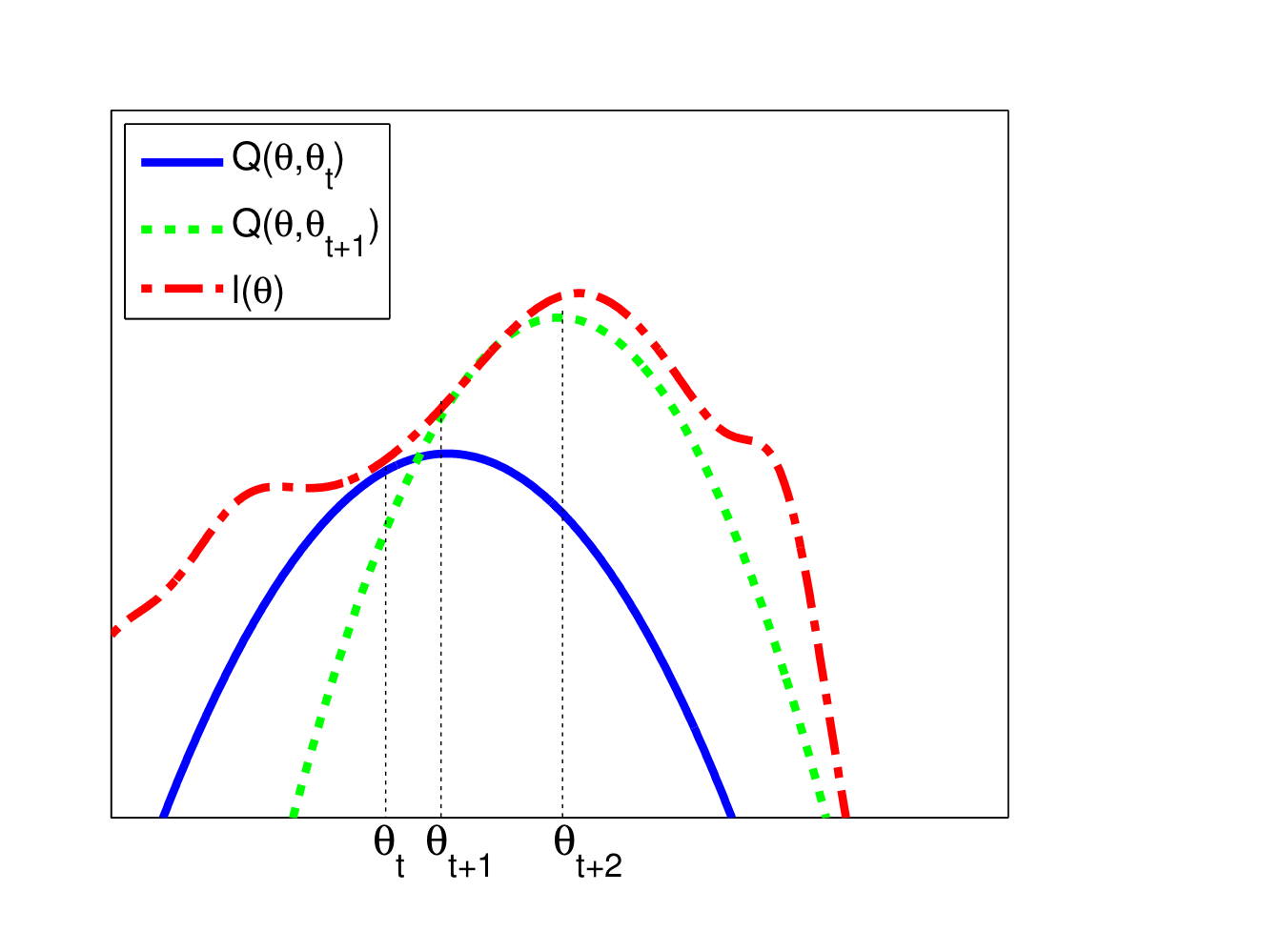
위 그림에서와 같이, $t$ 시점에서의 값 $\theta_{t}$ 에서의 surrogate function(파란색)을 찾고,해당 function을 최대로 하는 $\theta$를 다음 step의 값으로 설정하는 과정을 반복하면 함수의 local maximum과 local maximum에 대응하는 parameter를 찾을 수 있다.

Surrogate function을 찾는 방법에는 여러 가지 방법이 있을 수 있으나, 가장 쉽게 생각하면 Taylor expansion을 활용하여 구할 수 있다. 다음과 같은 Taylor expansion을 생각해보자.

여기서 g는 gradient vector, H는 Hessian matrix를 각각 의미한다. 그러면 위 taylor expansion으로부터 다음을 만족하는 negative definite matrix $B$를 찾을 수 있다.

이때 위 식의 좌변은 $\theta$에 대한 함수이므로, 우변의 함수를 $\theta$에 대한 것으로 간추리면 이로부터 다음과 같이 surrogate function을 도출할 수 있다.

또한, 위 surrogate function을 최대화하기 위해 $\theta$에 대해 미분하여 0이 되도록 하는 값을 찾으면 update 과정은 다음과 같이 나타난다.

Ex. Logistic Regression

Binary logistic regression에서 앞서 살펴본 MM algorithm이 어떻게 적용되는지 살펴보자. 우선 n번째 sample이 class $c\in \{1,2\}$ 에 포함될 확률은 각각

으로 주어진다. 이때 normalization condition, 즉 두 클래스에 속할 확률의 합이 1이라는 조건에 의해 $w_{2}=0$으로 두고 하나의 weight parameter만 구해도 무방하다. 이를 이용해 로그가능도를 구하면 다음과 같다.

여기서 $y_{n1}$은 $n$번째 관측치가 class 1인 경우 1의 값을 갖고 class 2인 경우 0의 값을 갖는다.
이를 바탕으로 Gradient를 구하면

과 같다. 또한, Hessian matrix의 lower bound는 다음과 같이 구해진다.

이를 바탕으로 계산한 Logistic Regression에서의 MM updating algorithm은 다음과 같다.

반면, IRLS(Iteratively reweighted Least Squares)로 구한 Updating algorithm은 다음과 같은데,
이를 비교해보면 MM algorithm에서의 inverse term은 단 한번만 계산해도 사용가능하므로 IRLS에 비해 전체적인 계산 속도가 빠를 수 밖에 없음을 확인할 수 있다.

Practice

Binary logistic regression에 대한 MM algorithm, IRLS algorithm을 직접 코드로 작성하여 실행해본 결과 속도차이를 확인할 수 있었다.

# MM algorithm for binary logistic regression

def MM(X, y, max_iter=1000, tol=1e-6):

start_time = time.time()

n, p = X.shape

beta = np.zeros(p)

Hessian = 4 * np.linalg.inv(X.T @ X)

  

for i in range(max_iter):

eta = X @ beta

mu = np.exp(eta) / (1 + np.exp(eta))

gradient = X.T @ (y - mu)

beta_new = beta + Hessian @ gradient

  

if np.linalg.norm(beta_new - beta) < tol:

break

beta = beta_new

  

return beta, time.time() - start_time

  

beta_hat_MM, time_MM = MM(X, y)

# Compare with iterative reweighted least squares

def IRLS(X, y, max_iter=1000, tol=1e-6):

start_time = time.time()

n, p = X.shape

beta = np.zeros(p)

  

for i in range(max_iter):

eta = X @ beta

mu = np.exp(eta) / (1 + np.exp(eta))

W = np.diag(mu * (1 - mu))

Hessian = X.T @ W @ X

gradient = X.T @ (y - mu)

beta_new = beta + np.linalg.inv(Hessian) @ gradient

if np.linalg.norm(beta_new - beta) < tol:

end_time = time.time()

break

beta = beta_new

return beta, end_time - start_time

  

beta_hat_IRLS, time_IRLS = IRLS(X, y)

print('MM algorithm: ', time_MM)
print('IRLS: ', time_IRLS)
# Result
# MM algorithm: 0.17301678657531738 IRLS: 1.429758071899414

References

• Probabilistic Machine Learning : Advanced Topics - K.Murphy
• Code on github : https://github.com/ddangchani/Velog/blob/main/Statistical%20Learning/MM%20algorithm.ipynb