[백준] 3085번 사탕 게임 in Kotlin

📜 문제

문제 링크

💡 나의 풀이

모든 사탕들에 대해 인접한 칸과 교환해보는 Brute Force 방식으로 문제를 풀었다.
이렇게 문제를 풀면 O(N^2 4 2N) = O(N^3)의 시간복잡도지만, n의 최댓값이 50이기 때문에 이 방식으로 문제를 해결할 수 있었다.

1. 모든 사탕들을 순회한다. (N^2)
   2. 현재 사탕과 인접해있는 사탕(상하좌우)과 교환해본다. (4)
      3. 현재 사탕의 행과 열을 순회하면서 모두 같은 색으로 이루어져 있는 연속 부분을 확인한다. O(2N)

3번 과정에 대해서 설명해보려고 한다.
다음 그림에서 (3, 2)위치에 있는 사탕과 그 사탕의 오른쪽(3, 3)에 있는 사탕과 교환하는 경우를 예시로 들어보자.

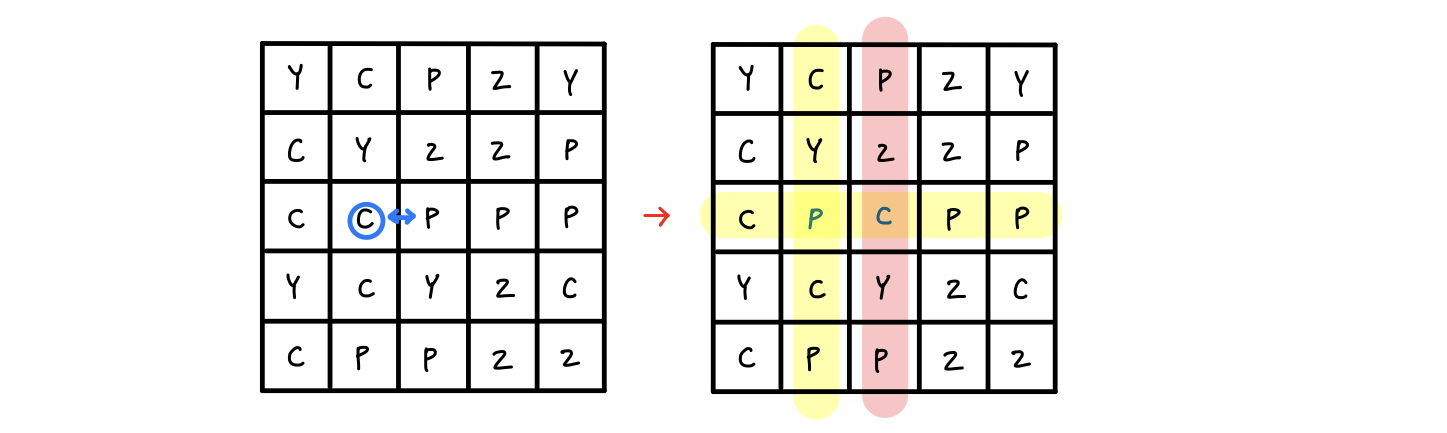
이 경우에 영향받는 행과 열은 오른쪽 그림에서 형광색으로 색칠한 부분임을 알 수 있다. 따라서 교환 후에 저 부분에 해당하는 부분만 같은 색이 연속으로 몇번 나오는지 확인하면 된다.
하지만 내 코드에서는 노란색 부분만, 즉 기존 위치(3행, 2열)의 부분만 확인하고 있다.
그 이유는 다음 그림으로 쉽게 이해할 수 있다.

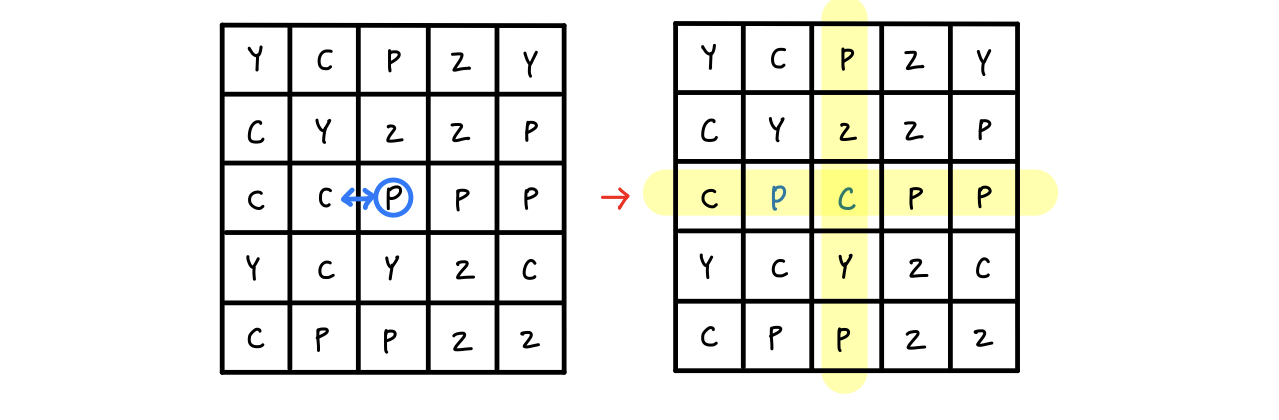
이후에 나오는 (3, 3)위치에 있는 사탕을 그 사탕의 왼쪽 사탕과 교환했을 때 확인하는 열이 위 그림의 빨간색 부분과 일치한다.
따라서 현재 사탕의 위치의 행과 열만 확인해도 되며, 오히려 중복으로 확인하지 않아도 되기 때문에 효율적이다.

⌨️ 코드

fun main() = with (System.`in`.bufferedReader()) {
        val n = readLine().toInt()
        val candies = Array(n) { charArrayOf() }

        for (i in 0 until n) {
            candies[i] = readLine().toCharArray()
        }

        var result = 0

        val dy = intArrayOf(-1, 0, 1, 0)
        val dx = intArrayOf(0, 1, 0, -1)
        
        //1. 모든 사탕들을 순회한다.
        for (i in 0 until n) {
            for (j in 0 until n) {
                //  2. 현재 사탕과 인접해있는 사탕과 교환해본다.
                for (d in 0..3) {
                    val changeY = i +dy[d]
                    val changeX = j + dx[d]

                    if (changeY in 0 until n && changeX in 0 until n) {
                        swap(candies, i, j, changeY, changeX)
                        // 3.현재 사탕의 행과 열을 순회하면서 모두 같은 색으로 이루어져 있는 연속 부분을 확인한다.
                        result = maxOf(result, countCandy(candies, i, j))
                        swap(candies, changeY, changeX, i, j)
                    }
                }
            }
        }

        println(result)
}

fun swap(candies: Array<CharArray>, i: Int, j: Int, k: Int, l:Int) {
        val tmp = candies[i][j]
        candies[i][j] = candies[k][l]
        candies[k][l] = tmp
}

// 3.현재 사탕의 행과 열을 순회하면서 모두 같은 색으로 이루어져 있는 연속 부분을 확인한다.
fun countCandy(candies: Array<CharArray>, i: Int, j: Int): Int {
        var iMax = 1
        var jMax = 1

		// i행 확인
        var count = 1
        for (k in 1 until candies.size) {
            if (candies[i][k] == candies[i][k - 1]) {
                count++
                iMax = maxOf(iMax, count)
            } else {
                count = 1
            }
        }

		// j열 확인
        count = 1
        for (l in 1 until candies.size) {
            if (candies[l][j] == candies[l - 1][j]) {
                count++
                jMax = maxOf(jMax, count)
            } else {
                count = 1
            }
        }

        return maxOf(iMax, jMax)
}

😄 느낀 점

2차원 배열 indexing하는 것이 아직 서투르다. 문제를 해결할 때 자꾸 헷갈려서 풀이시간이 오래걸리는 거 같다ㅠ🥲
다른 사람들의 풀이를 보니까 3번 과정에서 모든 행과 열에 대해서 연속하는 같은 색의 사탕들의 개수를 찾는 풀이가 많았지만, 두 사탕을 교환했을 때 영향받지 않는 부분에 대해서는 다시 확인할 필요가 없다고 생각했고 다행히 풀이방법을 찾아서 더 효율적으로 해결할 수 있었다. 하지만 중간에 인덱싱에 오타가 있어서 삽질을 오래 했지만 말이다😂