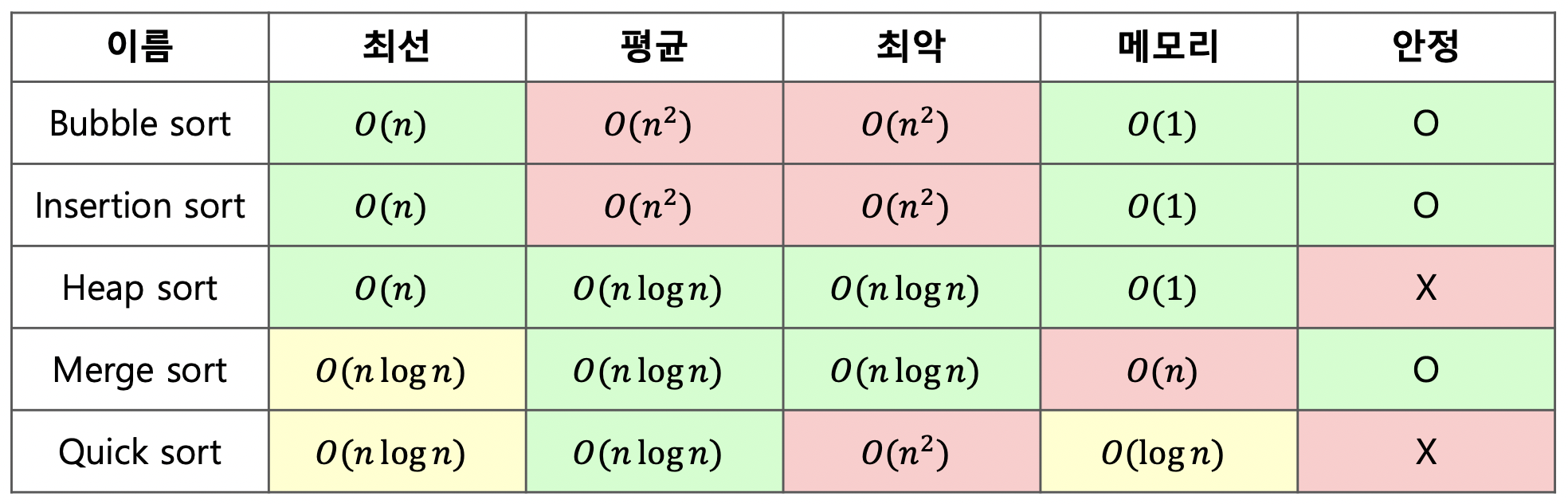
Sort의 종류
- Selection sort
- Bubble sort
- Quick sort
- Insertion sort
- Shell sort
- Merge sort
- Heap sort
Selection sort
현재 위치에 들어갈 값을 찾아 정렬하는 방식.
1. 정렬되지 않은 인덱스의 맨 앞에서부터, 이를 포함한 그 이후의 배열값 중 가장 작은 값을 찾아감.
2. 가장 작은 값을 찾으면, 그 값을 현재 인덱스의 값과 바꿔준다.
3. 다음 인덱스에서 위 과정을 반복
Bubble sort
매번 연속된 두개의 값을 비교하여 작은 값이 앞으로 큰 값을 뒤로 보내는 방식.
1. 현재 인덱스 값과 이전 인덱스 값을 비교
2. 만약 이전 인덱스가 더 크면 교환
3. 현재가 더크면 교환하지 않고 인덱스+1
4. 끝에 도달하면 다시 처음 인덱스부터 마지막 인덱스-1 까지 위 과정을 반복.
Quick sort
Divide and conquer를 이용하여 정렬을 수행
1. pivot point를 설정 - 보통 중간 값
2. pivot보다 작은건 왼쪽 큰건 오른쪽으로 넘김
3. 왼쪽과 오른쪽에 대해서 다시 pivot 정해서 진행 - recursive로
Insertion sort
현재 위치에서, 그 이하의 배열들을 비교하여 자신이 들어갈 위치를 찾아 그 위치에 삽입하는 방식
1. 두번째 인덱스를 현재 인덱스로 설정. 비교 인덱스를 현재 인덱스 -1로 설정
2. 현재 인덱스와 비교 인덱스를 비교해서 정렬
3. 비교 인덱스가 0이 되면 현재 인덱스를 +1해줌
Shell sort
삽입정렬을 보완한 알고리즘
1. 먼저 정렬해야 할 리스트에 gap을 설정하여 연속적이지 않은 여러개의 부분 리스트를 생성
2. 각 부분 리스트를 삽입정렬을 이용하여 정렬
3. 모든 부분 리스트가 정렬되면 다시 전체 리스트를 더 작은 gap의 부분리스트로 만든 후에 알고리즘 반복
4. gap이 1이 될때까지 반복.
Merge sort
Divide and conquer 방식을 이용하여 정렬을 수행.
1. 배열의 크기가 1보다 작거나 같을 때 까지 divide 수행
2. 가장 작은 단위의 배열 A, B의 각 index를 i, j로 놓고 A[i]와 B[j]를 비교해서 작은 것들 먼저 넣는 방식으로 다음 크기의 배열을 생성
3. 배열의 개수가 1개가 될때까지 conquer를 진행.
Heap sort
max heap tree나 min heap tree를 구성해 정렬을 하는 방식.
1. 정렬해야 하는 n개의 요소들로 max heap을 만든다
2. 0번 index의 값을 제일 마지막 index의 값과 변경
3. 마지막 index를 fix해놓고, 0, 1, 2번 index를 비교해서 제일 큰 값을 0번 index로 설정
4. 2 ~ 3 과정을 반복.