Linear regression 3 _ rice

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from scipy import stats
import statsmodels.api as sm

np.set_printoptions(precision=3, suppress=True)

fn = '1인당_연간_양곡소비량_20230324202553.csv'
np_data = pd.read_csv(fn, encoding='cp949').to_numpy()
print(np_data)

# [['용도별' '시점' '전가구 (kg)' '농가 (kg)' '비농가 (kg)']
#  ['주부식용' '2011' '69.8' '107.7' '67.2']
#  ['주부식용' '2012' '68.6' '105.4' '66.2']
#  ['주부식용' '2013' '66.0' '101.6' '63.1']
#  ['주부식용' '2014' '64.0' '99.0' '61.2']
#  ['주부식용' '2015' '61.9' '96.3' '59.4']
#  ['주부식용' '2016' '61.0' '94.7' '59.0']
#  ['주부식용' '2017' '61.1' '92.3' '59.3']
#  ['주부식용' '2018' '60.5' '91.7' '58.8']
#  ['주부식용' '2019' '58.6' '90.3' '56.9']
#  ['주부식용' '2020' '57.1' '88.8' '55.5']
#  ['주부식용' '2021' '56.5' '87.4' '54.9']
#  ['주부식용' '2022' '56.5' '87.4' '54.9']]

np_data = np_data[1:,1:].astype(np.float64)
print(np_data)

# [[2011.    69.8  107.7   67.2]
#  [2012.    68.6  105.4   66.2]
#  [2013.    66.   101.6   63.1]
#  [2014.    64.    99.    61.2]
#  [2015.    61.9   96.3   59.4]
#  [2016.    61.    94.7   59. ]
#  [2017.    61.1   92.3   59.3]
#  [2018.    60.5   91.7   58.8]
#  [2019.    58.6   90.3   56.9]
#  [2020.    57.1   88.8   55.5]
#  [2021.    56.5   87.4   54.9]
#  [2022.    56.5   87.4   54.9]]

< 목표 >

1. 농가와 비농가 사이의 회귀선 추정
2. 시점과 비농가 사이의 회귀선 추정
3. 농가와 비농가 중 더 빨리 감소 또는 증가하고 있는 것은

.
.
.
.
.

🛻 새로운 column 만들기

• '농가 + 비농가' column 만들기

a = np_data[:,2]
b = np_data[:,3]
col_sum = a+b   # 농가 + 비농가
print(col_sum.shape)   # (12, )
print(np_data.shape)   # (12,4)

기존의 np_data 가 2차원이기 때문에, '농가 + 비농가' column을 추가로 만들어주기 위해서는, 'col_sum' 도 2차원 데이터이여야지 np.contatenate가 가능하다.
따라서, np.newaxis을 사용하여, 'col_sum'을 1차원 -> 2차원으로 바꾸어준다.

col_sum = col_sum[:,np.newaxis]
print(col_sum.shape)   # (12,1)

이후, np.concatenate 를 이용하여, 데이터를 붙혀준다.

np_data_concat = np.concatenate((np_data, col_sum), axis=0)
print(np_data_concat)

# [[2011.    69.8  107.7   67.2  174.9]
#  [2012.    68.6  105.4   66.2  171.6]
#  [2013.    66.   101.6   63.1  164.7]
#  [2014.    64.    99.    61.2  160.2]
#  [2015.    61.9   96.3   59.4  155.7]
#  [2016.    61.    94.7   59.   153.7]
#  [2017.    61.1   92.3   59.3  151.6]
#  [2018.    60.5   91.7   58.8  150.5]
#  [2019.    58.6   90.3   56.9  147.2]
#  [2020.    57.1   88.8   55.5  144.3]
#  [2021.    56.5   87.4   54.9  142.3]
#  [2022.    56.5   87.4   54.9  142.3]]

• '농가의 비율 , 비농가의 비율' 각각 column 만들기

x = np_data_concat[:,2] / np_data_concat[:,4] # 농가비율
y = np_data_concat[:,3] / np_data_concat[:,4] # 비농가 비율

x = x[:, np.newaxis]
y = y[:, np.newaxis]

np_data_final = np.concatenate((np_data_concat, x, y), axis=0)
print(np_data_final)

# [[2011.      69.8    107.7     67.2    174.9      0.616    0.384]
#  [2012.      68.6    105.4     66.2    171.6      0.614    0.386]
#  [2013.      66.     101.6     63.1    164.7      0.617    0.383]
#  [2014.      64.      99.      61.2    160.2      0.618    0.382]
#  [2015.      61.9     96.3     59.4    155.7      0.618    0.382]
#  [2016.      61.      94.7     59.     153.7      0.616    0.384]
#  [2017.      61.1     92.3     59.3    151.6      0.609    0.391]
#  [2018.      60.5     91.7     58.8    150.5      0.609    0.391]
#  [2019.      58.6     90.3     56.9    147.2      0.613    0.387]
#  [2020.      57.1     88.8     55.5    144.3      0.615    0.385]
#  [2021.      56.5     87.4     54.9    142.3      0.614    0.386]
#  [2022.      56.5     87.4     54.9    142.3      0.614    0.386]]

🛻 농가와 비농가 사이의 회귀선 추정

x = np_data[:,2] # 농가
y = np_data[:,3] # 비농가

# 상관도
xy_corr = np.corrcoef(x,y)[0,1]
print(xy_corr)    # 0.9855025014693379

# 회귀선
fit_line = np.polyfit(x,y,1)
print(fit_line)              # [0.586 3.905]  <- 기울기, y절편
print(np.poly1d(fit_line))   # 0.586 x + 3.905

_,axe = plt.subplots()
axe.scatter(x,y)
axe.plot(x, fit_line[0]*x + fit_line[1])

» 농가와 비농가의 쌀소비량에 대한 상관계수는 0.9855 로 높은 양의 상관관계를 갖고 있으며, 회귀선을 추정하고 그려보면 양의 상관관계를 보이는 것을 알 수 있다.

🛻 시점과 농가 사이의 회귀선 추정

y = np_data[:,2]  # 농가
x = np_data[:,0]  # 시점

# 상관도
xy_corr = np.corrcoef(x,y)[0,1]   
print(xy_corr)    # -0.9760591450063468


# 회귀선
fit_line_farm = np.polyfit(x,y,1)
print(fit_line_farm)             # [  -1.869 3864.521]  <- 기울기, y절편
print(np.poly1d(fit_line_farm))  #  -1.869 x + 3865


_,axe = plt.subplots()
axe.scatter(x,y)
axe.plot(x, fit_line_farm[0]*x + fit_line_farm[1])

» 시점과 농가 사이의 상관계수는 -0.9760으로 높은 음의 상관관계를 보인다. 또한 회귀선을 추정하여 그려보면 위와 같이 나오므로, 음의 상관도를 보인다고 할 수 있다.

🛻 시점과 비농가 사이의 회귀선 추정

y = np_data[:,3]  # 비농가
x = np_data[:,0]  # 시점

# 상관도
xy_corr = np.corrcoef(x,y)[0,1]   
print(xy_corr)    # -0.9617129201426006


# 회귀선
fit_line_city = np.polyfit(x,y,1)
print(fit_line_city)             # [  -1.095 2267.979]  <- 기울기, y절편
print(np.poly1d(fit_line_city))  #  -1.095 x + 2268


_,axe = plt.subplots()
axe.scatter(x,y)
axe.plot(x, fit_line_city[0]*x + fit_line_city[1])

🛻 농가와 비농가 중 더 빨리 감소하고 있는 것은 ?

x = np.arange(2011,2200)

_, axe = plt.subplots()
axe.plot(x, fit_line_farm[0]*x + fit_line_farm[1], c='r')
axe.plot(x, fit_line_city[0]*x + fit_line_city[1], c='b')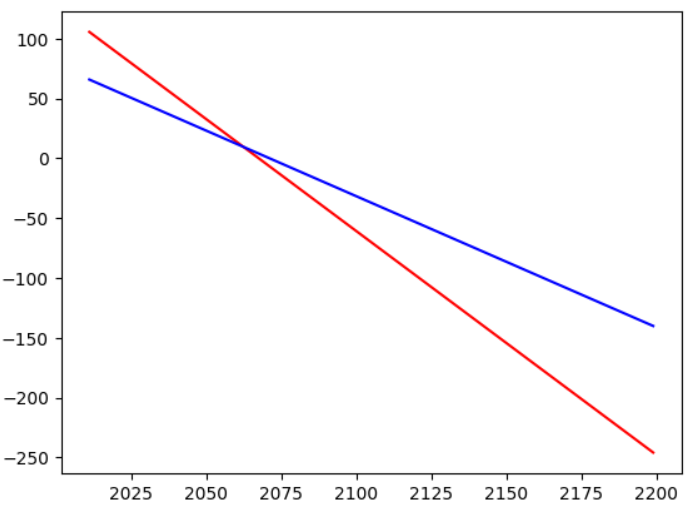

» 농가의 쌀 소비량이 비농가보다 더 많지만, 급격하게 감소하고 있기 때문에, 대략 2070년 쯤에 두 농가의 쌀 소비량이 같아질 것으로 예측하며 이후로는 농가의 쌀 소비량이 비농가보다 더 적을 것으로 예측된다.