Sklearn _ LinearRegression & SGDRegression

Scikit-learn 설치

!pip install scikit-learn

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns

from sklearn.model_selection import train_test_split  
# train, test data 로 나눠주는 함수
from sklearn.linear_model import LinearRegression, SGDRegressor
from sklearn.metrics import r2_score, mean_squared_error 
# 성능과 정확도 체크(r2_score, mean_squared_error)
from sklearn.datasets import load_diabetes 
# built-in data : 당뇨병환자 데이터

import load_diabetes 를 하여, scikit-learn에 내장되어 있는 diabetes(당뇨병) 데이터를 불러올 수 있다.

diabetes = load_diabetes()
print(diabetes)
print(diabetes.DESCR)

• Data Set Characteristics:
  :Number of Instances: 442

  :Number of Attributes: First 10 columns are numeric predictive values

  :Target: Column 11 is a quantitative measure of disease progression one year after baseline

  :Attribute Information:
  - age age in years
  - sex
  - bmi body mass index
  - bp average blood pressure
  - s1 tc, total serum cholesterol
  - s2 ldl, low-density lipoproteins
  - s3 hdl, high-density lipoproteins
  - s4 tch, total cholesterol / HDL
  - s5 ltg, possibly log of serum triglycerides level
  - s6 glu, blood sugar level
  

X, y = load_diabetes(return_X_y = True)
print(type(X),type(y))   # <class 'numpy.ndarray'> <class 'numpy.ndarray'>
print(X.shape, y.shape)  # (442, 10) (442,)

(big X : 2차원 / small y : 1차원)

🛻 LinearRegression

1. train/test set 으로 데이터 분할

X_train, X_test, y_train, y_test = train_test_split(X, y, random_state =10)

2. train data set 으로 linear regression

m = LinearRegression()  # linear regression을 수행하는 instant 를 활성화시킨 것.
m.fit(X_train, y_train) # 선형회귀 모델에 X_train, y_train 데이터를 적합.

print(m.coef_) #각 10개 feature에 대한 회귀계수 (기울기)
# [   6.7924784  -224.39685223  505.73935978  319.35318609 -776.39893593
#   396.87458108  132.80380166  308.91529418  689.37659909   53.89074748]
print(m.intercept_) #절편
# 151.79831831053397

_LinearRegression 수행 결과 :
target = 6.79 age - 224.39 sex + 505.73 bmi ... + 151.7983

3. $R^2$ 값

r2_score
y_test set 과 X_test set으로 예측한 y값을 비교하여 정확도를 평가할 수 있다.

# 방법 1. 
test_r2 = r2_score(y_test, m.predict(X_test))
print(test_r2)
# 0.5282320385429604

# 방법 2.
test_score = m.score(X_test, y_test)
print(test_score)
# 0.5282320385429604

---

---

간단하게, diabetes 의

bmi 로 당뇨병지수(target)를 예측

하는 model 을 만들어보자.

x_bmi = X[:,2]
print(x_bmi.shape)  # (442,)    # 1차원 배열

단, sklearn 의 X_train 은 2차원 배열이여야 하므로, 차원을 추가 해준다.

X_bmi = x_bmi[:,np.newaxis]
print(X_bmi.shape)  # (442, 1)  # 2차원 배열

.
.

1. train/test set 으로 데이터 분할

X_train, X_test, y_train, y_test = train_test_split(X_bmi, y, random_state =10)

2. train data set 으로 linear regression

m = LinearRegression().fit(X_train, y_train)
print(m.coef_, m.intercept_)
# [950.49561372] 152.91978688616442

3. plot

X_train 은 2차원 배열이므로, scatter plot 을 그리기 위해 다시 1차원으로 바꿔주어야 한다 : X_train[:,0]

X_train.shape
# (331, 1)

_,axe = plt.subplots()
axe.scatter(X_train[:,0], y_train)
axe.plot(X_train[:,0], 
         m.coef_ * X_train[:,0] + m.intercept_, 
         color ="y")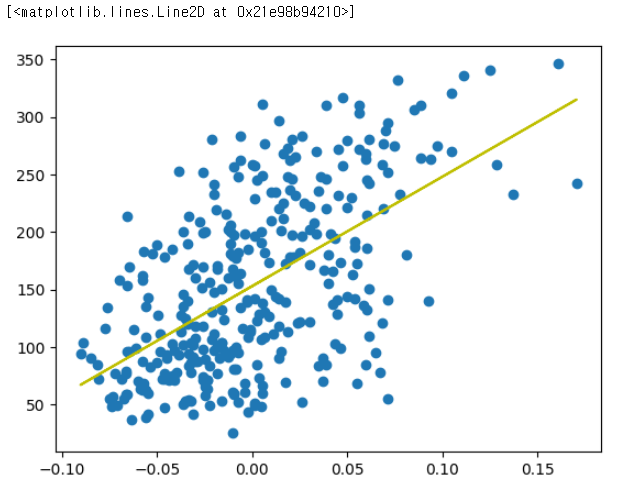

.
.

함수

• my_line : x 에 대한 예측값
• err : y 와 y_predict에 대한 오차
• sqerr : 오차 제곱합

def my_line(x, coef=1.0, intercept=1.0) :
    return x*coef + intercept

def err(y, y_pred) :
    return y - y_pred

def sqerr(y, y_pred) :
    return((y-y_pred)**2).sum()

위의 함수들을 이용하여,
1. bmi data 의 train set인 X_train[ : ,0] 을 이용하여, 당뇨병지수(target)의 예측값을 구하고,
2. 오차의 제곱합을 구해보자.

target_pred = my_line(X_train[:,0], m.coef_, m.intercept_)  # y_predict : 예측값
print(target_pred) 
# array([161.36343378, 121.40966349, 181.85254675,  94.77381662,
#         67.11351411, 164.43680073,  86.57817143, 143.94768776,
#        190.04819194, 223.85522835, 211.56176057, 170.58353462,
#        128.58085303, 143.94768776, 209.51284927, 166.48571203,
#        116.28738524, 122.43411913, 109.1161957 , 122.43411913,
#        123.45857478, 177.75472416, 210.53730492, 154.19224424,
#        169.55907897, 176.73026851, 109.1161957 , 187.99928065,
#                               ...
#                               ...
#        142.92323211, 185.95036935, 189.0237363 , 181.85254675,
#        135.75204257, 144.9721434 , 128.58085303])

print(sqerr(y_train, target_pred)) # train set 과 예측값 사이의 오차제곱합
# 1283841.7982087363

• 오차제곱합 : 1283841.7982087363

이 오차제곱합으로 예측모델의 좋고, 나쁨을 판단할 수 있는 기준은 ?

평균을 기준으로 구한 오차제곱합보다 예측값으로 구한 오차제곱합이 더 작아야한다.

def rsq(y, y_pred) :
    return 1 - (sqerr(y, y_pred) / sqerr(y, y.mean()))
# mean값 대비 얼마나 좋은 모델인가 ?

rsq(y_train, target_pred)
# 0.3322712894001999

1 에 가까울수록 mean 값대비 예측값이 더 좋다고 볼 수 있는데, 현재 모델은 10개 feature 중 bmi 만을 가지고 예측했으니, 당연히 예측력이 떨어질 수 밖에 없다. bmi 만을 가지고, 당뇨병지수를 예측하는 모델은 좋은 모델이 아니지만, 이해하기 쉽도록, 하나의 feature 만을 가지고 해보았다.
.
.
.
.
.

🛻 SGDRegression

SGDRegressor

X, y = load_diabetes(return_X_y = True)

X_train, X_test, y_train, y_test = train_test_split(X, y, random_state =10)

m = SGDRegressor(max_iter = 10000) 
#ConvergenceWarning : 수렴이 제대로 이루어지지 않음. -> max_iter = 1000(기본값) 이상으로 주기.
m.fit(X_train, y_train)

print(m.coef_) 
# [  36.68776932 -152.70374561  434.40387863  272.22859437  -30.54782152
#   -92.16888858 -202.50512974  160.82331369  357.91814085  113.52880264]
print(m.intercept_)
# [151.57134602]

test_r2 = r2_score(y_test, m.predict(X_test))
print(test_r2)
# 0.5074284303054717

SGDRegression 이 작용하는 방법

brute & back_prop

def brute(x, y, a = 1.0, b =1.0) : # 기울기 a, 절편 b
    y_hat = x*a + b
    while y - y_hat > 1:
        a = a + x
        b = b + 1
        y_hat = x*a + b
    return a, b

# 기울기와 절편의 초기값 = 1.0
# y 와 y_hat 의 차이(error) 가 1보다 클 동안
# 기울기와 절편을 조절
# 기존 기울기 + x
# 기존 절편값 + 1
# 내가 원하는 range(1) 안에 들어올 때까지 기울기와 절편을 계속 수정.
# forward 방법의 시간이 너무 오래걸린다는 단점을 극복하기 위해 나온 것이 역전파 방법


# 역전파
def back_prop(x,y, a=1.0, b=1.0) :
    y_hat = x*a +b
    err = y - y_hat
    a = a + x*err
    b = b + 1*err
    return a, b

# 가장 큰 차이 : err 값을 a 값과 b 값을 구하는데, 사용함 ! 

SGDRegression 이 진행되는 방법 _ 시각화

_,axe = plt.subplots()
xs = np.linspace(-0.1, 0.15, 10)  # bmi 값의 범위
bmi = X[:,2]
target = y

axe.scatter(bmi[0], target[0], c = 'g')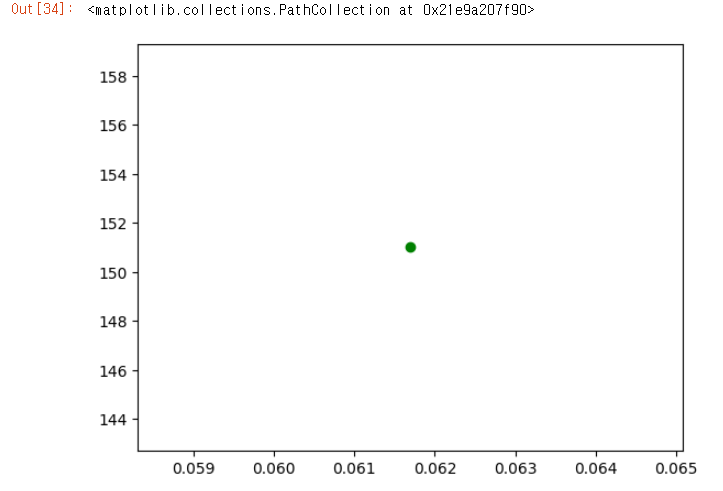

a1, b1 = brute(bmi[0], target[0])
print(a1, b1)  # 10.192734771283801   150.0
axe.plot(xs, my_line(xs, coef = a1 , intercept = b1))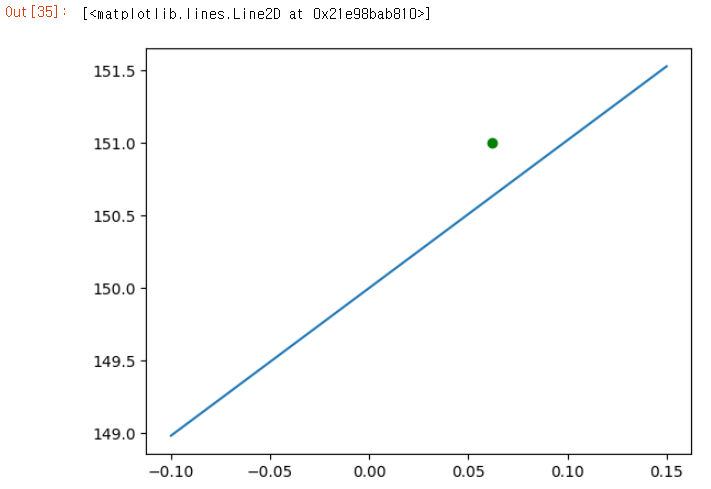

# 역전파 방법
a2, b2 = back_prop(bmi[0], target[0])
print(a2, b2) # 10.250624555903698   150.9383037934813
axe.plot(xs, my_line(xs, coef = a2, intercept = b2))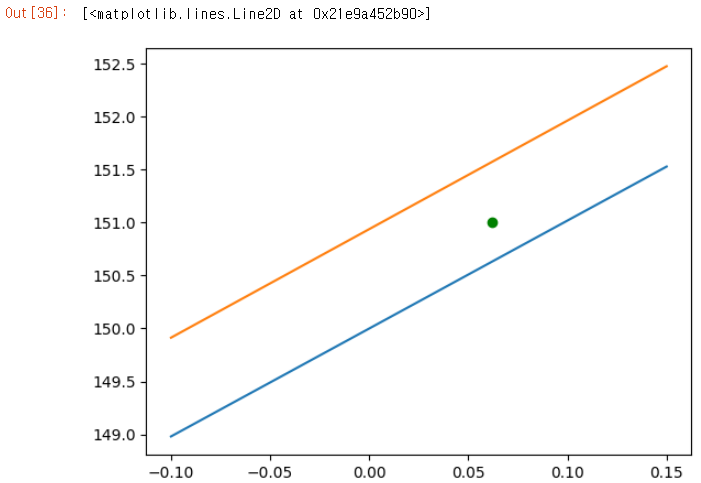

SGDRegression : a (회귀계수) 와 b (절편) 의 움직임 시각화

( epoch = 1 )

a = 1.0
b = 1.0
hist_a = []
hist_b = []

for i in range(bmi.shape[0]):
    a, b = back_prop(bmi[i], target[i], a, b)
    hist_a.append(a)
    hist_b.append(b)
print(a, b) # 587.8654539985616   99.4093556453094

_, axe = plt.subplots()
axe.scatter(bmi, target)
axe.plot(bmi, bmi*a+b)

_, axe = plt.subplots()
axe.plot(hist_a)
axe.plot(hist_b, c='r')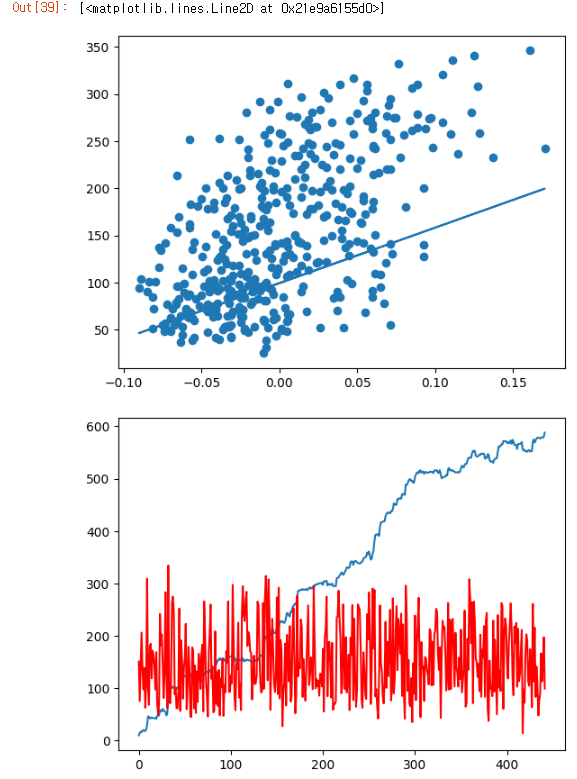

( epoch = 50 )

a = 1.0
b = 1.0
hist_a = []  #a의 움직임 list
hist_b = []  #b의 움직임 list
hist_sqerr = []  #

for e in range(50):
    for i in range(bmi.shape[0]):
        a, b = back_prop(bmi[i], target[i], a, b)
    hist_a.append(a) # epoch가 1씩 증가할 때마다, a 값을 list에 append
    hist_b.append(b) # epoch가 1씩 증가할 때마다, b 값을 list에 append
    t = np.array(target)
    m = np.array(my_line(bmi, a, b))
    hist_sqerr.append(sqerr(t, m))
print(a, b) # 913.5973364346786   123.39414383177173

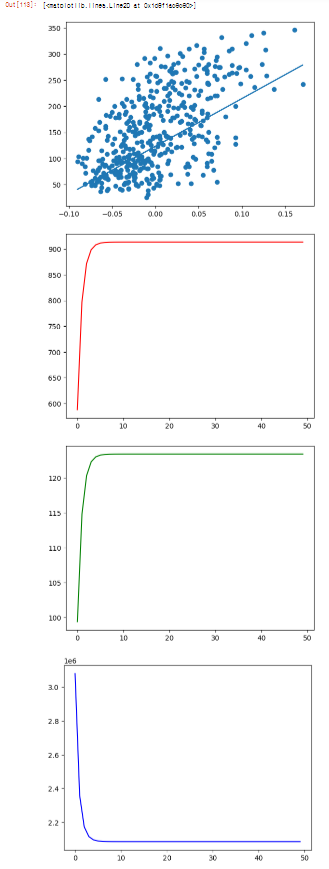
_, axe = plt.subplots()
axe.scatter(bmi, target)
axe.plot(bmi, bmi*a+b)

# epoch 를 높혔을때, 좋아지는 한계가 있다. 정답은 없고, 데이터에 따라 다르기 때문에 몇번을 주는 것이 알맞은 건지는 나중에 meterparameter 로 조절해주어야 함.

# 기울기와 절편의 변화
_, axe = plt.subplots()
axe.plot(hist_a, c= 'r')

_, axe = plt.subplots()
axe.plot(hist_b, c='g')

_, axe = plt.subplots()
axe.plot(hist_sqerr, c='b')  # sqerr 값이 변화하는 곡선의 기울기(radient) 를 보는 것이 gradient descent
                             # 기울기가 높은 곳에서 낮은 곳으로 내려옴
                             # 기울기가 0 에 가깝도록

# epoch = 50 은 너무 과한 설정이다. epoch 는 대략 10 정도로만 주어도 충분함.