✨ 문제
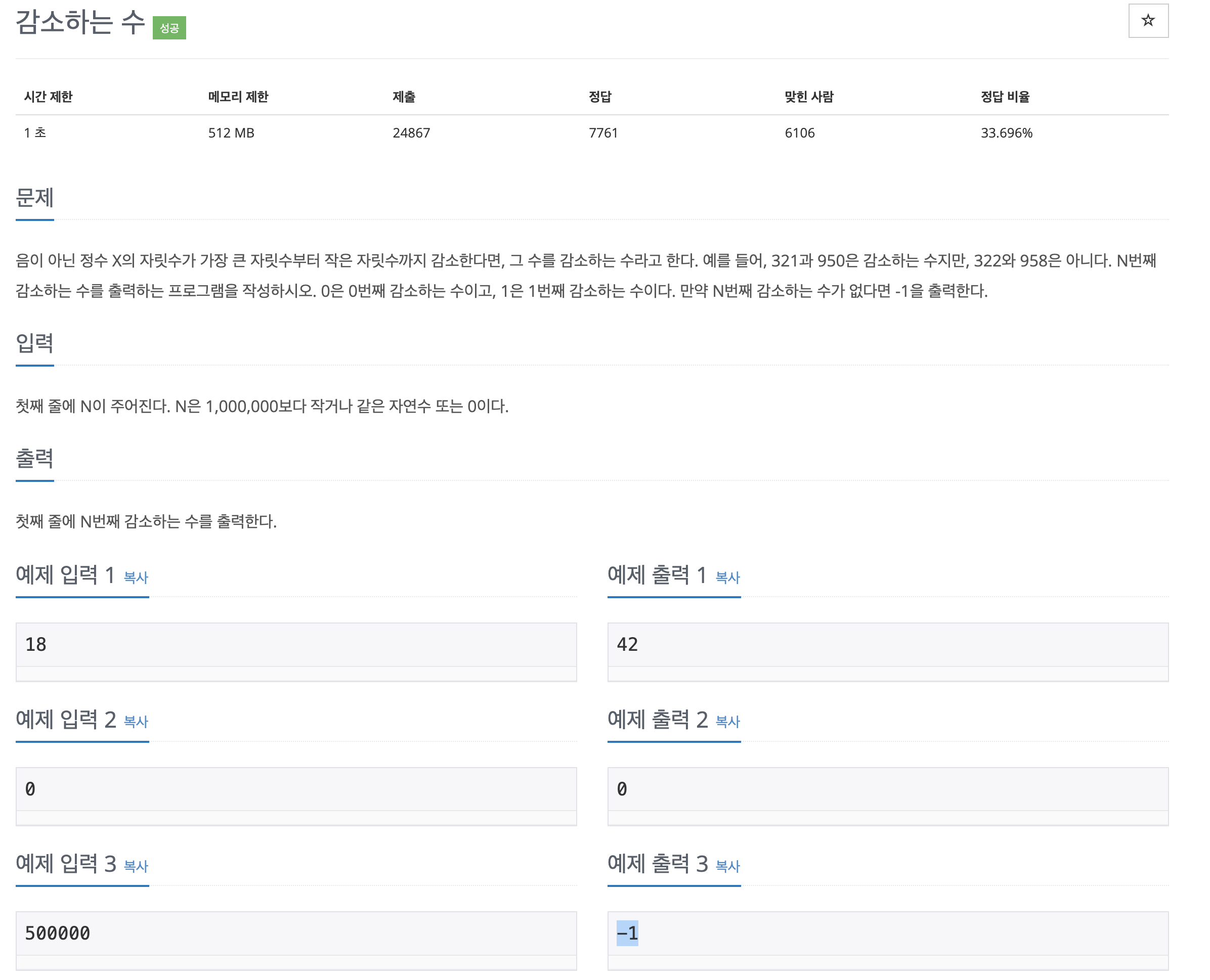
문제 링크 → 백준 1038번 - 감소하는 수
✨ 주의할 점
- 0~9의 한자리 수 또한 감소하는 수이다.
- 0번째 감소하는 수는 0이라는 점이다. (1번째 감소하는 수 != 0)
- 322에서 22와 같이 같은 숫자가 연속되어도 감소하는 수라 볼 수 없다.
✨ 풀이
collection 모듈 combinations 이용
1부터 차례대로 1씩 늘려가며 해당 숫자가 감소하는 수인지 판단하기는 너무 시간이 오래 걸릴 것 같아 숫자 길이 단위로 나눠보려고 사용한 방식이다.
ex) N = 10 → 길이가 1인 감소하는 수를 make_decreasing_num 함수가 리스트로 리턴한 결과 0,1,2,3,4,5,6,7,8,9 10개이므로 아직 답을 구하지 못하고 길이가 2인 감소하는 수를 찾아 나서는 과정으로 푸는 것이다.
from itertools import combinations
def make_decreasing_num(length):
re = []
li = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
for comb in combinations(li, length):
comb = list(comb)
comb.sort() # (2, 1, 3)과 같은 조합이 등장할 경우 감소하는 수를 만들기 위해 (1, 2, 3)으로 만들어주는 것과 같다.
num = 0
for y, j in enumerate(comb):
num += j * pow(10, y)
re.append(num)
re.sort() # N번째 감소하는 수를 알기 위해서는 감소하는 수 리스트가 오름차순으로 정렬되어 있어야 한다.
return re
if __name__ == "__main__":
N = int(input())
num = []
result = -1 # N번째 감소하는 수가 없을 때 출력할 값을 저장해두기
for i in range(1, 11):
num.extend(make_decreasing_num(i))
if(len(num) > N):
result = num[N]
break
print(result)- main 부분에서는 N을 입력받고 길이가 i인 감소하는 수 리스트를 make_decreasing_num으로 구해 num 리스트에 추가한 후, 다음 길이로 넘어가기 전에 num 리스트의 길이와 N을 비교해 N번째 감소하는 수가 포함된 num 리스트가 만들어지면 break하여 나오고 그렇지 않으면 다음 반복으로 넘어가도록 했다.
- make_decreasing_num 함수는 combinations를 이용해 li에서 length개의 원소를 골라 조합을 만든 후, 해당 조합을 오름차수 정렬하여 숫자로 변환한 뒤 리스트에 넣어주는 과정을 반복한다. 이후 감소하는 수가 모인 리스트를 정렬해 리턴한다.
dfs 이용
dfs를 이용하는 방식은 위 방식으로 풀고 제출한 후, 다른 사람들의 풀이를 보다가 괜찮은 것 같아서 해당 방식으로 풀어본 코드이다.
N = int(input())
num = []
def make_decreasing_dfs(number):
num.append(number)
units = int(str(number)[0])
for i in range(units+1, 10):
make_decreasing_dfs(int(str(i)+str(number)))
for i in range(10):
make_decreasing_dfs(i)
if len(num) > N:
num.sort()
print(num[N])
else:
print(-1)- dfs 핵심 = 재귀 & 종료 조건
- 여기서는 0~9까지의 i가 반복적으로 make_decreasing_dfs를 호출하고, 해당 함수는 재귀적으로 호출되며 계속해서 감소하는 수를 찾아 리스트 num에 append한다. 함수는 계속해서 반복하다 units가 9일 때, 즉 인자로 넘어온 수의 가장 맨 앞에 있는 숫자가 9일 때 리턴된다.
✨ 결과
combinations 이용한 코드

dfs 이용한 코드

👩🏻💻 후기
문제를 보고 든 생각은 1부터 세기는 시간이 너무 오래 걸리겠다..와 자릿수를 기준으로 나눠서 구해볼까..였다. 후자의 생각이 combinations를 떠올리게 하는데까지 오래 걸려서 문제였지만,, 이 문제를 풀었으니 앞으로 combinations를 잘 활용해봐야겠다. 또, 문제를 풀고 다른 사람 코드를 봤을 때 dfs 방식도 쓸 수 있구나 생각이 들어서 작성해본 코드도 꽤 괜찮은 것 같다. 실제로 시간도 조금 더 빨랐기 때문이다. 대신 dfs는 자릿수가 아니라 0~9까지의 베이스 숫자를 가지고 감소하는 수를 만들어 확장해나가는 방식이다. 바로 저번 학기에 알고리즘 수업을 들었는데, 이때 배운 dfs를 떠올리며 코드를 작성해봤다. 마지막으로 이 문제는 2년 전에.. 그니까 신입생인 1학년 때 도전했다가 실패해서 남겨둔 문제인데 이번에 풀게 되어서 의미가 컸다!