오일러 경로(Eulerian Path)와 오일러 회로(Eulerian Circuit)

1. 오일러 경로와 회로

: directed/undirected graph에 존재하는 모든 간선을 1번씩만 방문하는 연속된 경로
이때 시작점과 도착점이 같으면 오일러 회로 가 된다.

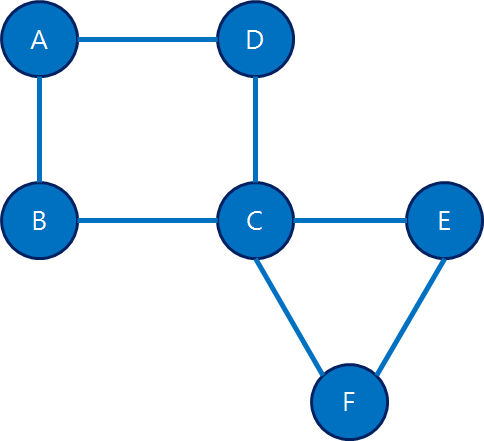
위 그래프에서 경로 [A, B, C, E, F, C, D, A] 는 오일러 회로이다.
모든 간선을 한번씩만 거치고 A -> A로 돌아갔기 때문이다.

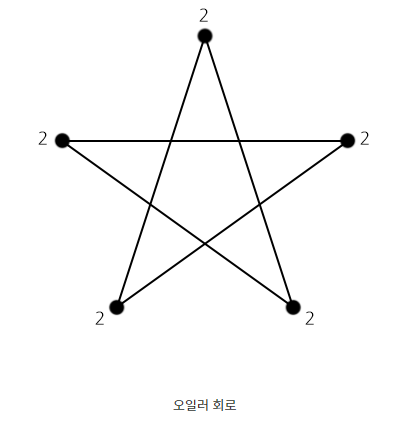
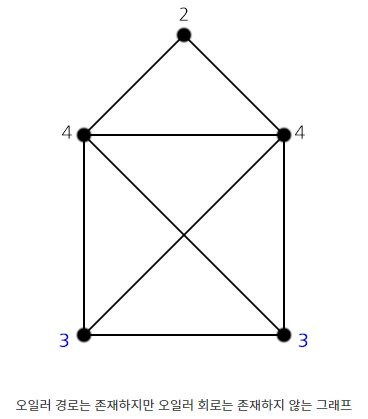
2. 오일러 경로의 존재성

오일러 경로의 존재성은 다음 두 조건중 하나를 만족해야 한다.

1. 모든 노드의 차수가 짝수이다.
2. 두 노드의 차수가 홀수이고, 나머지 노드는 모두 차수가 짝수이다.

여기서 차수란

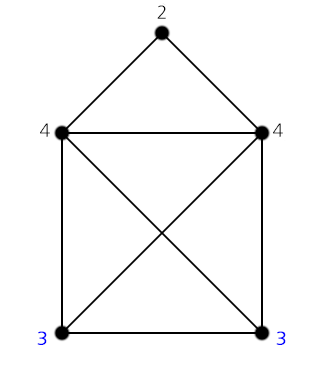
정점에 부속되어 있는 간선의 수를 차수 라고 한다.

undirected graph 일 경우 차수가 홀수인 정점 c가 2개일 때 오일러 경로가, 0개일 때 오일러 회로가 존재한다.

3. 오일러 회로 구하기

Hierholzer's Algorithm 을 사용해 구해보자.

1. 아무 정점 v를 뽑고 v에서 출발하여 v로 돌아오는 경로를 하나 선택한다.
2. 이때, 위 경로에 속해있는 정점 중에서 인접한 간선들 중 경로에 쓰이지 않은 (방문하지 않은 간선이 있는) 정점 u가 존재하면, u에서 시작해 쓰이지 않은 간선들만 사용해 u로 돌아오는 경로를 찾아 원래 경로에 끼워 넣는다.

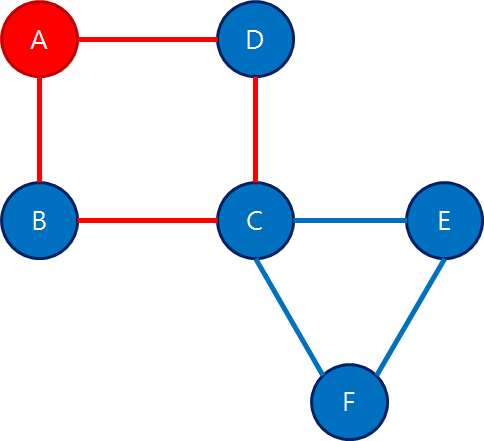
위 그래프에서 시작점을 A로 놓고 경로 [A, B, C, D, A]를 찾았다고 하자.
그러나 이 중 정점 C는 아직 사용하지 않은 인접한 간선이 존재한다.

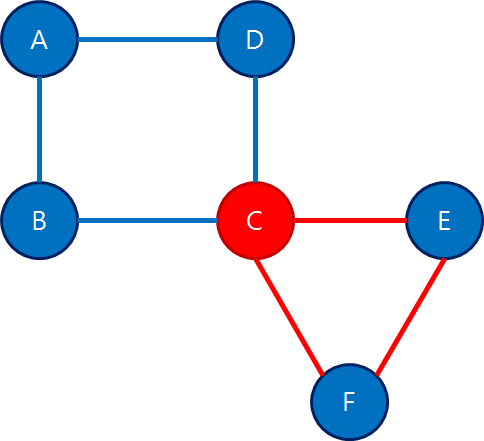
따라서 C에서 또다른 경로 [C, E, F, C]를 찾아서 원래의 경로에서 C가 있던 자리에 대체해서 끼워 넣으면, [A, B, C, E, F, C, D, A]가 되어 오일러 회로가 완성된다.

또 경로 [C, E, F, C]의 정점들 중에서 아직 사용하지 않은 인접간선이 남아있는 정점이 존재한다면 재귀적으로 또 경로를 구해 끼워넣는다.

4. 구현 [C++]

#include<iostream>
#include<vector>

using namespace std;

#define NODE 7
#define INF 9999999

int adjMat[NODE][NODE];

void addEdge(int u, int v) {
	adjMat[u][v]++;
	adjMat[v][u]++;
}

vector<int> path;
void eulerPath(int here) {
	for (int there = 0; there < NODE; there++) {
		while (adjMat[here][there]) {
			adjMat[here][there]--;
			adjMat[there][here]--;
			eulerPath(there);
		}
	}
	path.push_back(here);
}

int main() {
	memset(adjMat, 0, sizeof(adjMat));

	addEdge(0, 1);
	addEdge(1, 2);
	addEdge(2, 3);
	addEdge(3, 4);
	addEdge(4, 5);
	addEdge(2, 5);
	addEdge(2, 6);
	addEdge(0, 6);
	addEdge(1, 3);

	// 1, 3번 노드의 차수가 홀수이므로 1 혹은 3 에서 시작.
	eulerPath(1);
	
	for (int node : path) {
		cout << node << ' ';
	}
}

---

💗 출처 :

• https://m.blog.naver.com/PostView.naverisHttpsRedirect=true&blogId=kks227&logNo=220800097205
• https://rain-bow.tistory.com/entry/%EC%98%A4%EC%9D%BC%EB%9F%AC-%EA%B2%BD%EB%A1%9C%EC%99%80-%ED%9A%8C%EB%A1%9CEulerian-trail-circuit