-
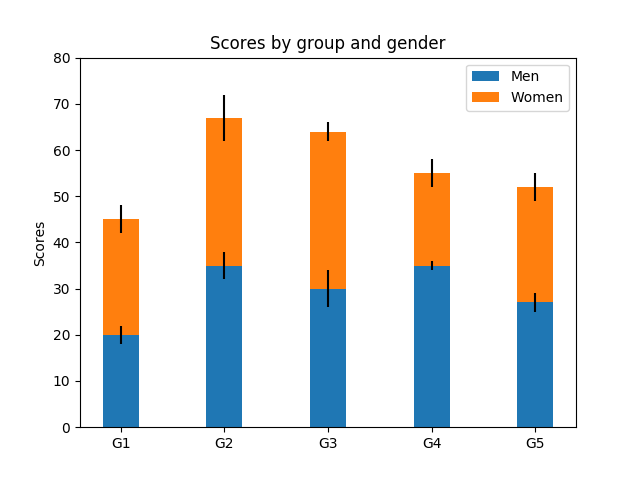
barplot, 이산형 자료에 대해 범주별로 빈도나 합계 등을 비교하는 데에 유용하다.
-
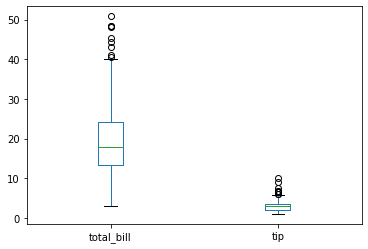
df[['total_bill','tip']].plot(kind='box')
tmp = '12,578'을 정수 12578로 변환하는 코드
#tmp,를 공백으로 바꿔준 뒤에 정수로 변환
int(tmp.replace(tmp[2],""))
#tmp를 , 기준으로 나눈 다음에 다시 합쳐주기
a,b = tmp.split(",")
int(a+b)

변환코드
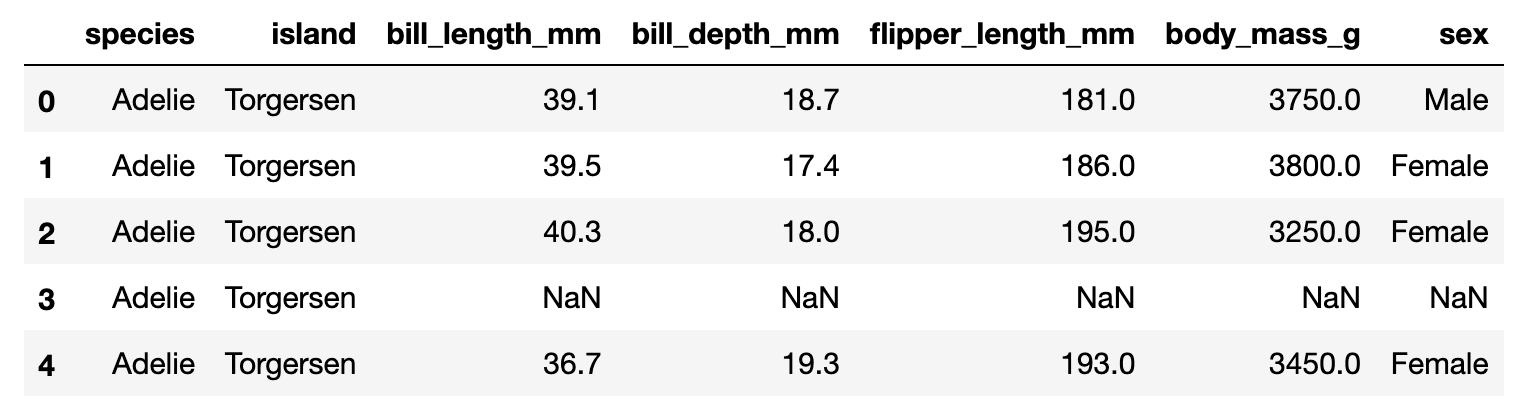
df.groupby('sex')['species'].count()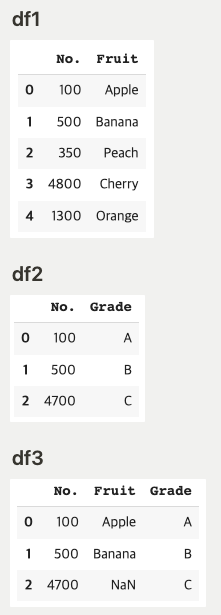
pd.merge(df1, df2, on='No.',how='right')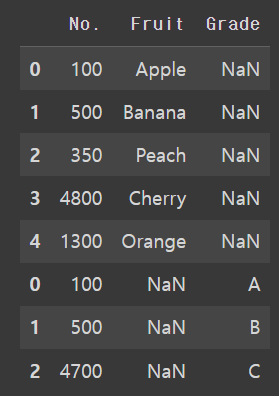
# df1 에다가 df2그냥 가져다가 사용
df1.append(df2)
pd.concat([df1,df2])append 세로로만 결합가능 is the specific case (axis=0, join='outer')of concat
concat 가로, 세로 모두 결합 가능 gives the flexibility to join based on the axis(all rows or all columns)
join is based on the indexes(set by set_index)on how variable = ['left','right','inner','counter']
merge is based on any particular column each of the two dataframes, this columns are variables on like 'left_on','right_on','on'
p-value
- p-value가 0에 가까울수록 대립가설이 힘을 얻는다.
- p-value는 0과 1사이의 확률이다.
- p-value를 통합 귀무가설이 맞다는 전제하여 simulation을 진행한다.
- p-value는 sample size와는 무관하다.
- 귀무가설 :null hypothesis
- 단측검정 : One-sided T-test
- 양측검정 : Two-sided T-test
중심극한정리 큰 수의 법칙
- 중심극한 정리 Central Limit Theorem : 어떠한 모양의 임의의 분포에서 추출한 표본집단들의 평균의 분포는 정규분포를 이룬다.
- 큰 수의 법칙 Law of Large Numbers : 어떤 모집단에서 표본집단들을 추출할 때, 각 표본집단의 크기가 커지면 그 표본집단들의 평균은 모집단의 평균과 같아지고, 표본집단들의 분산은 0에 가까워 진다.
암에 걸릴 확률은 1% 이고, 암 검사가 정확히 암을 양성이라고 진단할 확률은 90% 입니다. 또한 암이 아닌데 양성이라고 진단할 확률은 10%입니다. 어떤 사람이 암 검사 결과에서 양성 반응이 나타났을 때, 실제로 이 사람이 암에 걸렸을 확률을 구하는 공식은 아래와 같습니다.
링크텍스트
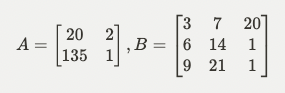
- 2개의 데이터 셋이 동일한 연관성을 가지지만, 공분산 값이 다를 수 있다.
- 어느 벡터이던 단위 벡터의 선형 조합으로 나타낼 수 있다.
- 상관계수의 절대값은 1을 넘을 수 없다.
K-means clustering을 실행하기 전, 데이터에 Data Standardization 필수 진행