#데이터사이언스 데이터와 행렬
링크텍스트
martix
- 수 또는 변수를 ()안에 행과 열로 배열
- 2차원 형태의 array 또는 list로 나타냄
- 행과 열의 개수는 매트릭스의 차원을 의미 .shape을 통해 확인
- 두 매트릭스 일치 = 차원과 성분이 동일해야 함.
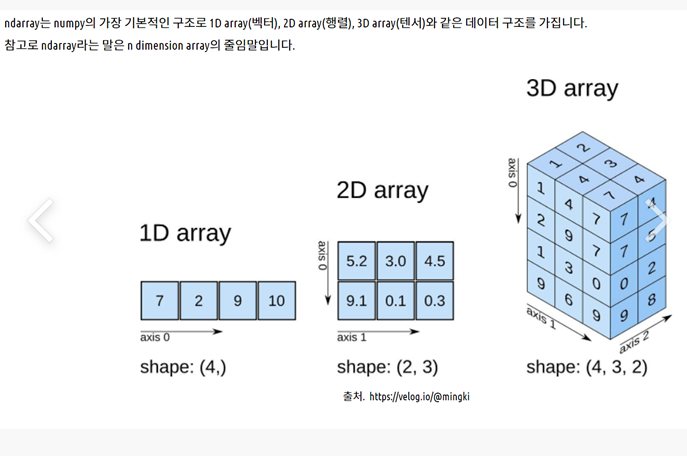
.ndim
- 배열의 차원 확인
.shape
- 벡터의 차원 확인
- 콤마 앞의 수는 벡터의 차원, 즉 성분의 개수
2d = np.array([[1,2,3],[4,5,6]])
2d
>>array([[1, 2, 3],
[4, 5, 6]])#.ndim을 사용하여 배열의 차원확인
2d.ndim
>> 2#.shape을 사용하여 매트릭스의 차원(행의 수, 열의 수)확인
2d.shape
>>(2,3)
# 1차원일 경우 #1d = np.array([1,2,3,4,5])
1d.shape
>>(5, )행렬의 연산
행렬의 전치 Transpose
- 행과 열을 바꾸어 나타내는 것입니다.
- 일반적으로 로 표기합니다.
.T또는np.transpose()를 사용하여 구할 수 있습니다.- 전치의 전치는 자기 자신입니다.
a=np.array([[1,2,3],[4,5,6]])
a
>>array([[1, 2, 3],
[4, 5, 6]])a.T
>>array([[1, 4],
[2, 5],
[3, 6]])(a.T).T
>>array([[1, 2, 3],
[4, 5, 6]])#np.transpose(a)
>>array([[1, 4],
[2, 5],
[3, 6]])행렬곱Matrix Multiplication
- 두 행렬에 대해서 앞 행렬의 열과 뒷 행렬의 행의 수가 같으면 행렬끼리 곱할 수 있습니다.
np.matmul()을 사용하여 구할 수 있습니다.- 행렬곱의 결과는 행렬입니다.
- 두 행렬의 차원이 , 이면 행렬곱으로 얻은 행렬의 차원은 입니다.

정사각형 행렬Square Martix
대각 행렬 Diagonal Martix
: 주 대각선(principal diagonal)을 제외한 모든 성분이 0인 정사각 행렬
단위 행렬Identity Matrix
- 대각 행렬 중에서 주 대각선 성분이 모두 1인 매트릭스
np.identity()또는np.eye()를 사용하여 나타낼 수 있습니다
- 임의의 정사각 행렬에 단위 행렬을 곱한 것은 자기 자신과 같습니다.
np.identity()와 np.eye()의 차이
역행렬
np.linalg.inv()사용하여 역행렬 구함.
np.multiply() 행령의 요소 별 곱셈
: 행렬의 특정 행, 열 또는 부분 행렬의 요소 별 곱셈을 수행
np.linalg.matrix_rank()
np.linalg.matrix_rank(A, tol=None)
: Return matrix rank of array using SVD method
링크텍스트