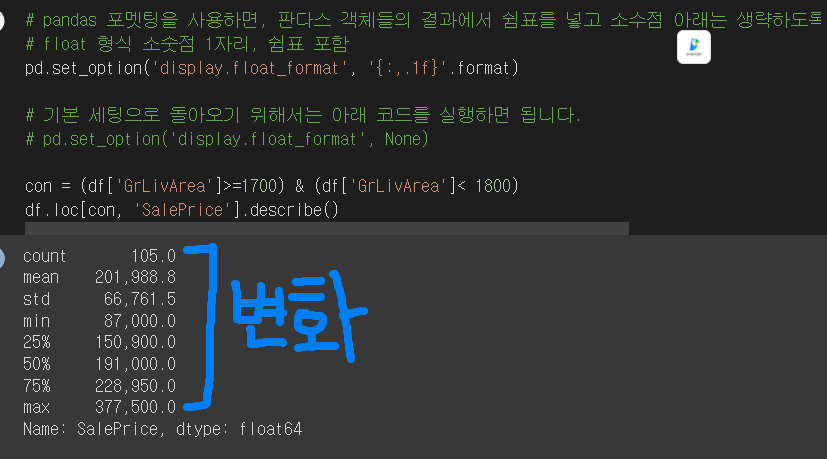
#con에서 지상생활면적이 1700보다 크고 1800보다 작은 값에서 가격을 비교
con = (df['GrLivArea']>=1700) & (df['GrLivArea']< 1800)
df.loc[con, 'SalePrice].min().set_option
#판다스 객체들의 결과에서 쉼표를 넣고 소수점 아래는 생략하도록 설정할 수 있습니다.
#float 형식 소숫점 1자리, 쉼표 포함
pd.set_option.display.float_format = '{:,.1f}'.format
pd.set_option('display.float_format', '{:,.1f}'.format)#기본세팅
pd.set_option('display.float_format',None)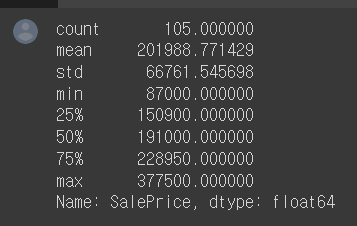
distplot
kind = ' histplot', 'kdeplot', 'ecdfplo' 3가지 plot그릴 수 있음
kde(Kernel Density Estimator) 커널밀도추정 = 곡선화 시켜 줌
산점도에 가장 잘 맞는 직선을 그려주면 그것이 회귀
회귀선 : 실제값- 모델의 예측값[잔차] RSS를 최소로 하는 직선 찾기
RSS : 선형회귀모델의 비용함수. 모델을 학습한다: 비용함수를 최소로 하는 파라미터를 찾는 것.
OLS : Ordinary Least Square : 최소제곱법, 잔차의 제곱을 최대한 작게함.
sns.regplot
추세선 95% 신뢰구간을 나타냄
종속변수는 반응(Response)변수, 레이블(Label), 타겟(Target)등으로 불립니다.
독립변수는 예측(Predictor)변수, 설명(Explanatory)변수, 특성(feature) 등으로 불립니다.
scikit-learn 이용해서 선형회귀모델 만들기
특성행렬(독립변수) = X 타겟배열(종속변수) = y
.fit() : 모델학습 predict() : 새로운 데이터 예측
다중선형회귀
from sklearn.linear_model import LinearRegression
#feature과 target을 먼저 지정해줌
feature = ['GrLivArea', 'OverallQual']
target = 'SalePrice'
X=df[feature]
y=df[target]- 3차원 그래프 그리는 것도 해보기 ~ 라고 미뤄두기 😉
변수 3개 2차원 그래프 그리기
#독립변수 하나를 hue로 지정해줌
#size
sns.scatterplot(x=dff['GrLivArea'], y=df['SalePrice'], hue=df['OverallQual'], size=df['OverallQual'], alpha=0.6)#모델학습
multiple_ols = LinearRegression()
multiple_ols.fit(X,y)다항선형회귀
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import PolynomialFeatures
## PolynomialFeatures를 사용하면 다항회귀를 만들 수 있습니다.
#degree=2 이차항
def PolynomialRegression(degree=2, **kwargs)
return make_pipline(PolynomialFeatures(degree)),
LinearRegression(**kwargs))
features = ['GrLivArea', 'OverallQual']
target = 'SalePrice'
X = df[features]
y = df[target]
#2차항의 다항선형회귀
poly_ols = PolynomialRegression(degree=2)
poly_ols.fit(X,y)링크텍스트
pipeline : 데이터변환(전처리)과 모델을 연결하여 코드를 줄이고 재사용성 높임
scaler를 불러오고 , fit, transform한 후 모델을 학습하는 일련의 작업이 있었지만 pipeline 을 사용하면 단순히 어떤 스케일러를 쓰고 모델을 쓸것인지만 입력하면 됨
make_pipeline : 여러 개의 사이킷런 변환기(fit, transform)와 그 뒤에 fit와 predict를 구현한 사이킷런 추정기 연결
따로 튜플로 단계를 작성할 필요가 없다. 모델만 써줘도 자동으로 class 이름을 소문자로 생성
링크텍스트
회귀 평가지표
- MSE RMSE MAE R-sqaured
from sklearn.metrics import r2_score, mean_absolute_error, mean_squared_error
# 실제값
y_real = df['SalePrice']
#기준모델
y_base = [predict]*len(df)#단순선형회귀 모델 학습
simple_ols = LinearRegression()
simple_ols.fit(X,y)
feature = ['GrLivArea'] #독립변수 입력
X_simple = df[feature] #X에 독립변수 넣어주기
y_simple = simple_ols.predict(X_simple) #학습한 x로 y값 예측#다중선형회귀 모델학습
multiple_ols = LinearRegression()
multiple_ols.fit(X,y)
features = ['GrLivArea', 'OverallQual']
X_multiple = df[features]
y_multiple = multiple_ols.predict(X_multiple)
#다항선형회귀
y_poly = poly_ols.predict(X_multiple)- 헷갈리는 부분 꼭 확인하기 함수 !!!
#위에서 y_real = df['SalePrice'] #종속변수
#mse, rmse, mae, r2[error]를 출력하는 함수입니다.
# 여기서 y_pred가 밑에 y_base,y_simple가 들어가는 건가?? 뭐지
def eval_models(y_pred, y_real=y_real):
mse = mean_squared_error(y_real, y_pred)
rmse = np.sqrt(mse) #제곱근
mae = mean_absolute_error(y_real, y_pred)
r2 = r2_score(y_real, y_pred)
return mse, rmse, mae, r2#평가지표 값
base_mse, base_rmse, base_mae, base_r2 = eval_models(y_base) #기준모델
simple_mse, simple_rmse, simple_mae, simple_r2 = eval_models(y_simple)
multiple_mse, multiple_rmse, multiple_mae, multiple_r2 = eval_models(y_multiple)
poly_mse, poly_rmse, poly_mae, poly_r2 = eval_models(y_poly)# 표만들기
comparison_metrics = pd.DataFrame(index=['mse', 'rmse', 'mae', 'r2'], columns=['Base','Simple', 'Multiple', 'Polynomial'])
comparison_metrics['Base'] = [base_mse, base_rmse, base_mae, base_r2 ]
comparison_metrics['Simple'] = [simple_mse, simple_rmse, simple_mae, simple_r2]
comparison_metrics['Multiple'] = [multiple_mse, multiple_rmse, multiple_mae, multiple_r2]
comparison_metrics['Polynomial'] = [poly_mse, poly_rmse, poly_mae, poly_r2]
comparison_metrics선형회귀모델의 계수 Coefficients
- 선형회귀모델의 큰 장점: 직관적 해석이 가능
coef_
#다중선형회귀
#회귀계수
print("coefficient :", multiple_ols.coef_)
## 절편(intercept)
print('Intercept : ', multiple_ols.intercept_)