벡터

Scalar

• 하나의 숫자(실수)를 나타냅니다.
• 변수에 저장하여 표기할 수 있습니다.
• 양수, 음수 모두 가능합니다.

  $a = 5 \quad b = 1.81 \quad c=-3e \quad d=\pi$

스칼라와 벡터

• 스칼라 : 크기
• 벡터 : 크기 + 방향이 존재

Vector

• 순서를 갖는 1차원 형태의 배열로 list 또는 array로 나타냅니다. #2개면 2차원 3개면 3차원 ...
• 헤드부분이 벡터의 성분을 향해서 있음
• 성분의 개수는 벡터의 차원을 의미합니다.

  \begin{align} \vec{a} = \begin{bmatrix} 8\\ 9 \end{bmatrix} \qquad \vec{b} = \begin{bmatrix} -4\\ 7\\ 1 \end{bmatrix} \qquad \vec{c} = \begin{bmatrix} 5.5332 \end{bmatrix} \qquad \vec{d} = \begin{bmatrix} Pl\\ x\\ y\\ \frac{2}{3} \end{bmatrix} \end{align}

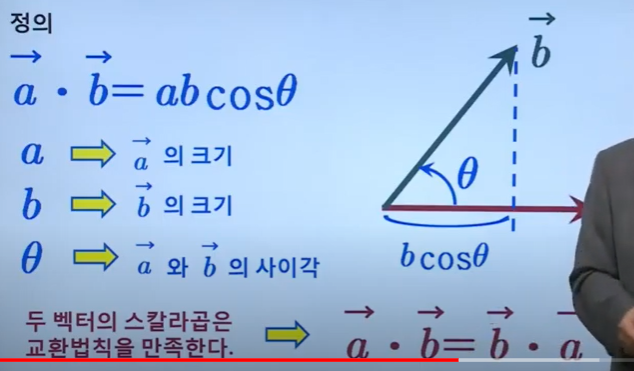
  벡터의 스칼라곱

  스칼라 + 스칼라 => 스칼라
  스칼라 스칼라 => 스칼라 (#스칼라는 숫자)
  스칼라 + 벡터 => 더하기 불가능 (같은 종류만 가능함)
  스칼라 벡터 => 벡터
  벡터 + 벡터 => 벡터
  벡터 * 벡터 => 스칼라
  벡터 (중간에 x 표시)
  텐서
  
  

  직각좌표계 단위벡터들 사이의 스칼라곱

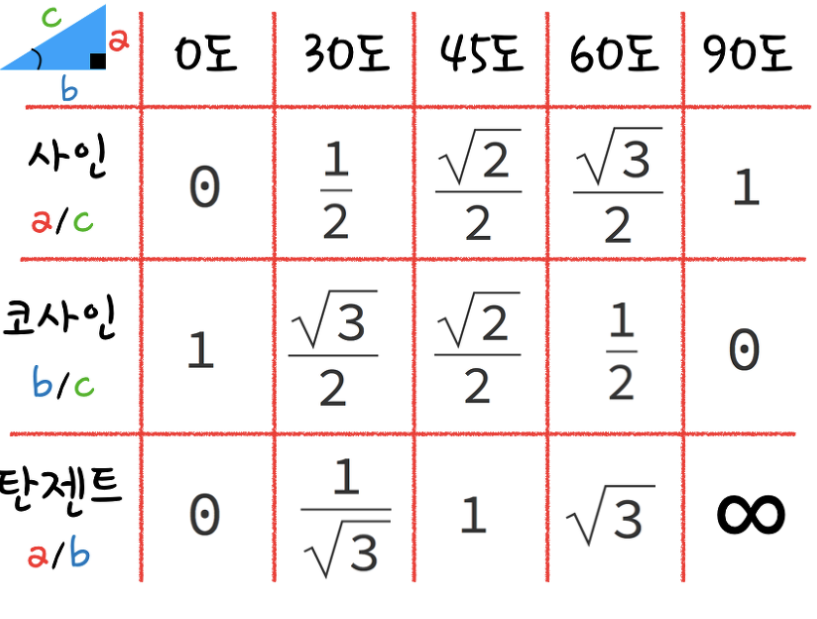
• 같은 단위벡터들 사이의 스칼라곱은 1
• 다른 단위벡터들 사이의 스칼라곱은 0

직교하는 두 벡터와 스칼라곱

직교는 스칼라 곱으로 판단

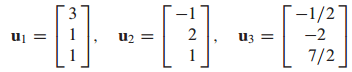
벡터의 크기

• 벡터의 선의 길이 = 벡터의 크기

• Norm 혹은 length, Magnitude라고 합니다.

• 벡터의 길이를 나타냅니다. 따라서 음수가 될 수 없습니다.

• 벡터의 모든 성분이 $0$이면 벡터의 크기도 $0$입니다. ;영벡터 : 방향을 고려하지 않음

• 벡터의 크기를 나타내는 기호 : $||v||$와 같이 표기합니다.
  - 값이 1이라면 단위벡터 : 크기가 1로 조정, 방향을 나타내는 데 집중함.

• 피타고라스 정리를 사용하여 구할 수 있습니다.
  

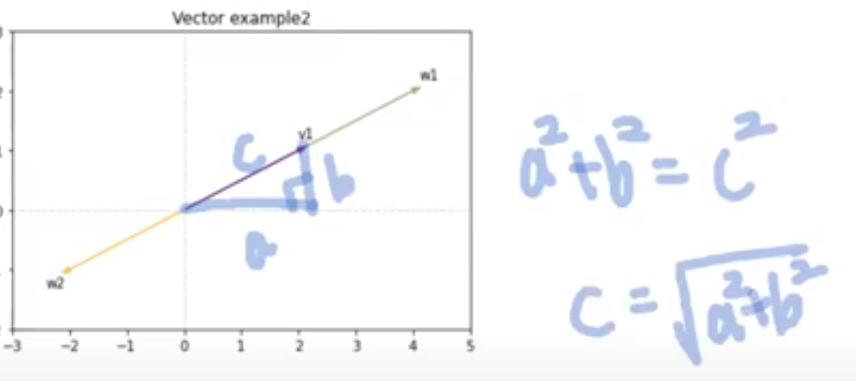
• 두 벡터가 서로 같을 조건
  - 크기와 방향이 동일하면 위치와 상관없음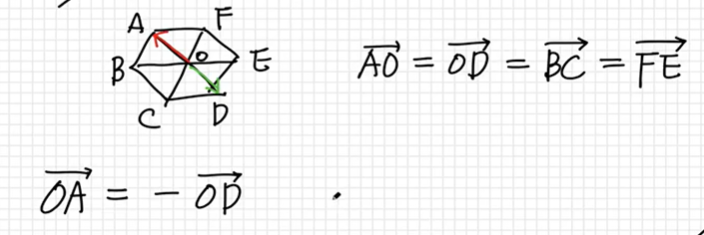

  • 
  • - 는 방향이 반대임을 나타냄

$v = [a, b, c, \cdots]$

$||v|| = \sqrt{a^2 + b^2 + c^2 + \cdots}$

벡터의 내적

• Dot Product라고 합니다.
• 두 벡터에 대해서 서로 대응하는 [인덱스가 같은 값]각각의 성분을 곱한 뒤 모두 합하여 구합니다. 이때 두 벡터의 차원이 같아야 합니다.[성분의 개수가 달라 짝이 맞지 않으면 내적 불가능]
• np.dot()을 사용해 구할 수 있습니다.
• 벡터를 내적한 값은 스칼라입니다.
  $v_1 = [a_1, a_2, a_3, \cdots]$

$v_2 = [b_1, b_2, b_3, \cdots]$

$v_1 \cdot v_2 = a_1b_1 + a_2b_2 + a_3b_3 + \cdots$

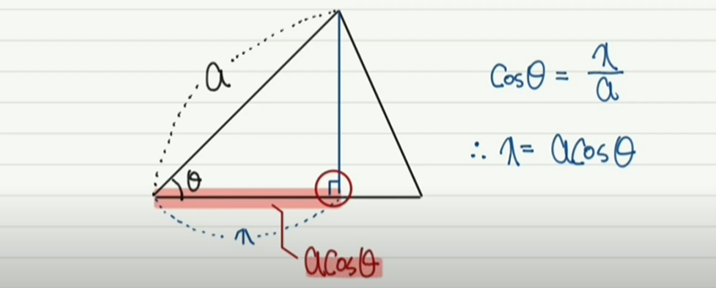
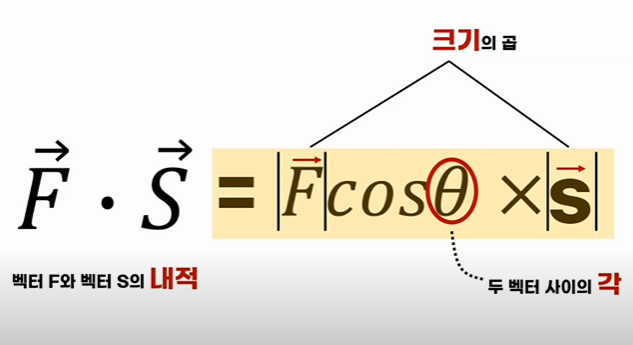
: 벡터 F와 벡터 S의 내적은 두개의 벡터의 크기를 곱한 후 cos을 곱한 값

• 벡터를 내적한 값 = 스칼라

벡터의 직교(Orthogonality) : 두 벡터의 내적이 0이면 두 벡터는 서로 수직입니다.

• 영벡터가 아닌 두 벡가 직교하기 위한 필요충분조건은 a· b=0
  

링크텍스트

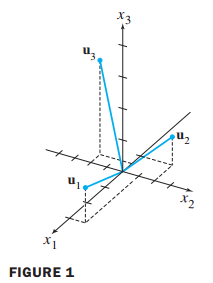
단위 벡터 Unit Vector

• 길이가 $1$인 벡터입니다.
• 모든 벡터는 단위 벡터의 선형 결합으로 표기할 수 있습니다.

  $v = [2,5] = [2,0] + [0,5] = 2[1,0] + 5[0,1] = 2\hat{i} + 5\hat{j}$
  [2,5]는 [2,0] + [0,5] 의 합임
  [2,0] 은 2[1,0] 이고 [0,5]은 5[0,1]라고 나타낼 수 있다.
  여기서[1,0] hat{i},[0,1] hat{j}은 단위가 1인 단위벡터가 된다.
  💡Tip
  -크기가 $1$인 길이를 단위 길이(unit length)라고 합니다.
  -선형 결합(linear combination) : 벡터 $v_1, v_2, \cdots, v_n$와 스칼라 $a_1, a_2, \cdots, a_n$에 대하여 다음과 같이 벡터의 스칼라곱과 합으로 나타낸 것입니다.

  $a_1v_1 + a_2v_2 + \cdots + a_nv_n$