Cryptography review 1

https://www.coursera.org/learn/crypto/home/week/1
강의 바탕으로 정리함.

cryptography는 어디에서나 있다

secure communication

web traffic: HTTPS, S == Secure
wireless traffic: 802.11i WPA2

encrypting files on disk:

EFS

Content protection(e.g. DVD):

CSS, AACS

ex. DRM(Digital RIght Management): dvd player에 dvd를 삽입하면 region key를 인식함. 아시아 거는 아시아에서만 재생 가능하다

Secure communication

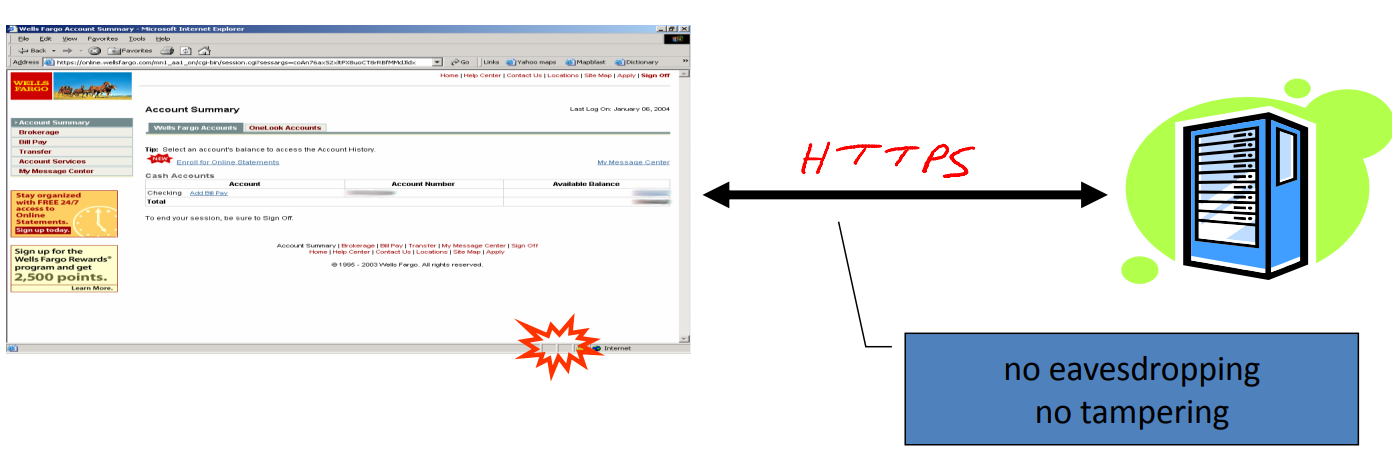
eavesdropping: 보는 것
tampering: 날라감

=> 암호화를 통하여 보는 것을 막고, 날라가지 못하게 함

정보 보안의 3대 요소(CIA)

confidentiality: 기밀성
Prevent unauthorized reading of information
-> 인가되지 않은 사람이 정보를 읽으면 안 된다.

Integrity: 무결성
detect unauthorized writing of information
-> 인가되지 않은 사람이 정보를 수정하면 안 된다.

Availability: 가용성
Data is available in a timely manner when needed
->데이터는 필요시에 항상 사용 가능해야 한다.

Protected files on disk

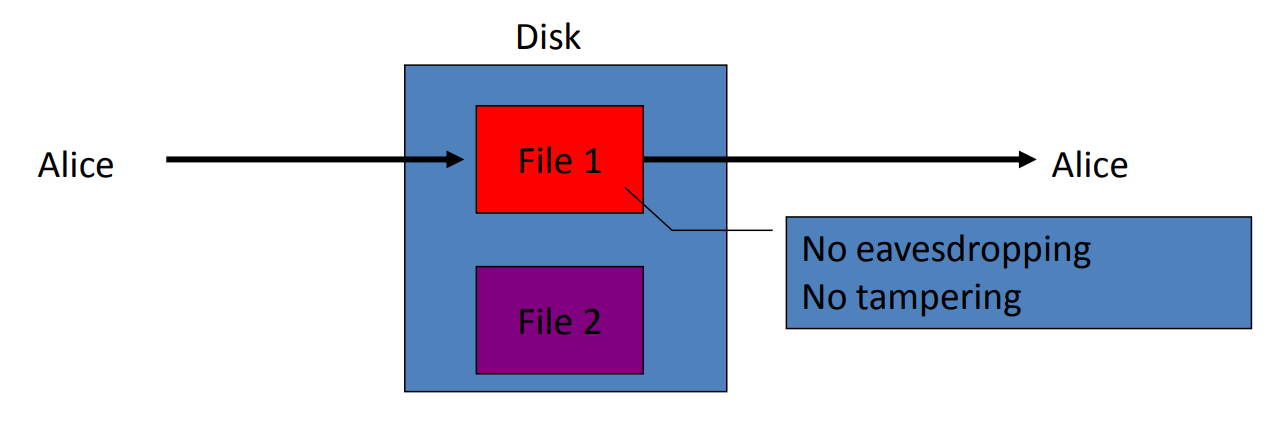
Sender = 오늘의 Alice가 데이터를 저장하고,
Receiver = 내일의 Alice가 데이터를 읽음

저장된 데이터는 암호화를 통하여 보는 것을 막고, 날라가지 못하게 함

Building block: sym.encryption

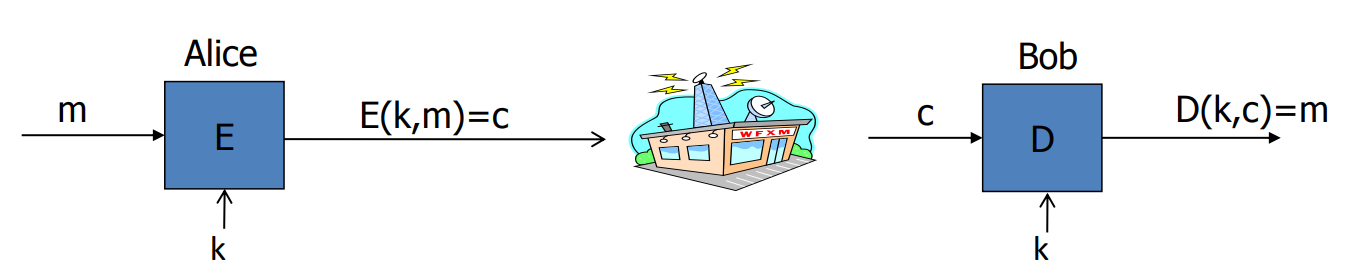
m = plaintext
c = ciphertext
Encyption, Decryption: cipher
k = secret key

여기서 세 가지 알고리즘이 적용된다.
Gen: key k를 만들기 위한 key generator
Enc: key k와 message m을 이용해 cipher text c를 만들어내는 encryption algorithm
Dec: key k와 cipher text c를 이용해 message m을 복호화 하는 decryption algorithm

Use Cases

Single Use Key: 일회성

알고리즘이 간단하다
encrypted email: new generated for every email

Multi Use Key: 다회성

알고리즘이 복잡하다
encryted files: same key used to encrypt many files

Things to remember

암호 != 해킹(보안)

그렇기 때문에 모든 보안 문제를 해결할 수 없다.
또한 꼼꼼하게 제대로 훈련하지 않는 이상, 모든 암호는 뚫릴 수밖에 없다.

Crypto Core

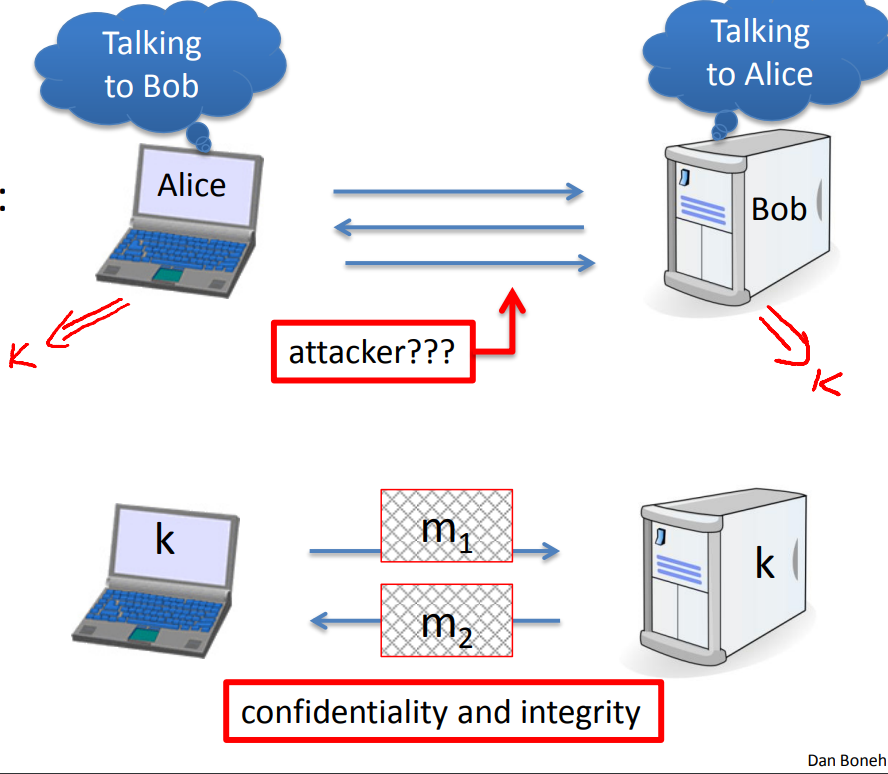
Secret Key establishment:
공유된 키가 없기에 public key or asymmetry key를 통하여 똑같은 키를 만든다. 느리다는 단점이 있다.

Secure communication:
symmetry 키를 써서 무결성과 기밀성을 지킨다. 일반적으로 빠르다.

ex. 디지털 서명, 익명 소통, 익명 디지털 캐시(ex. 블록체인)

• Anonymous digital cash:
  ex. 예를 들어 서점에서 책을 사는 경우에는, 나는 책을 샀지만 서점에게는 인식을 하지 못하도록 하여 개인정보는 가리고 보내야 할 책만 인식하게 한다.

Protocols

• Elections

• Private auctions

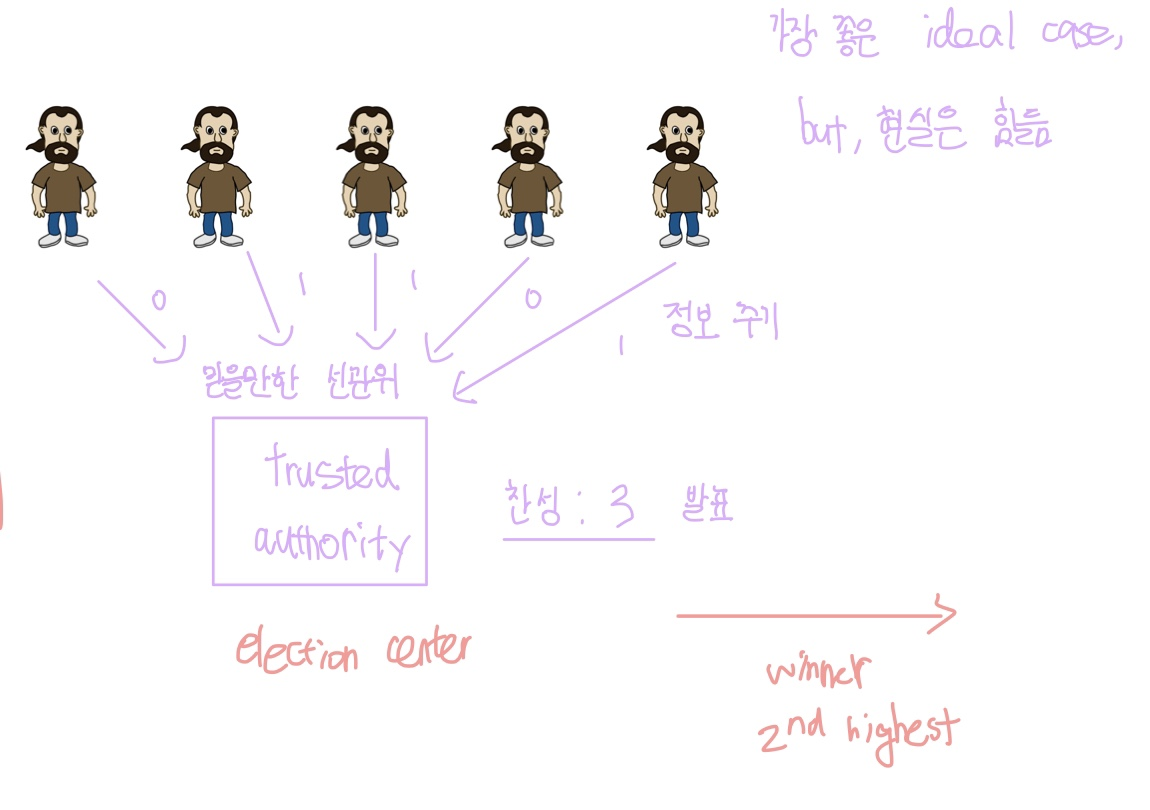
현실의 attacker가 있을 수도 있으니 trusted auth 없이도 할 수 있는 것 => Secure multi-party computation

Crypto magic

• Privately outsourcing computation
  

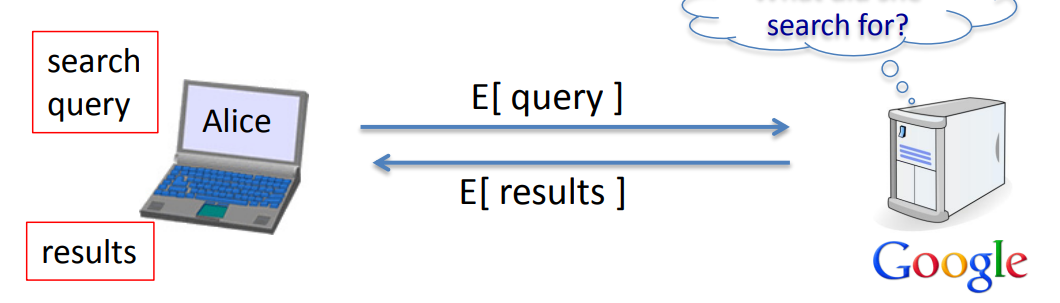
개인정보를 원하지 않는 경우, 암호화된 쿼리를 제공한다. 그러면 이것을 받고, 암호화된 것을 처리하고 다시 Alice에게 준다.

• Zero Knowledge(영지식 증명)
  암호학에서 누군가가 상대방에게 어떤 사항(statement)이 참이라는 것을 증명할 때, 그 문장의 참 거짓 여부를 제외한 어떤 것도 노출되지 않는 interactive한 절차를 뜻한다.
  

N의 인수값은 알지만, p,q는 알려주지 않아서 모른다.

A Rigorous Science

• Precisely specify threat model
• Propose a construction
• Prove that breaking construction under threat mode will solve an underlying hard problem

어려운 문제가 있으면 공격자를 통해 문제를 풀 수 있음을 증명한다. 못 풀 경우에는 이 알고리즘을 푸는 공격자가 없다고 정의한다.

Symmetric Ciphers

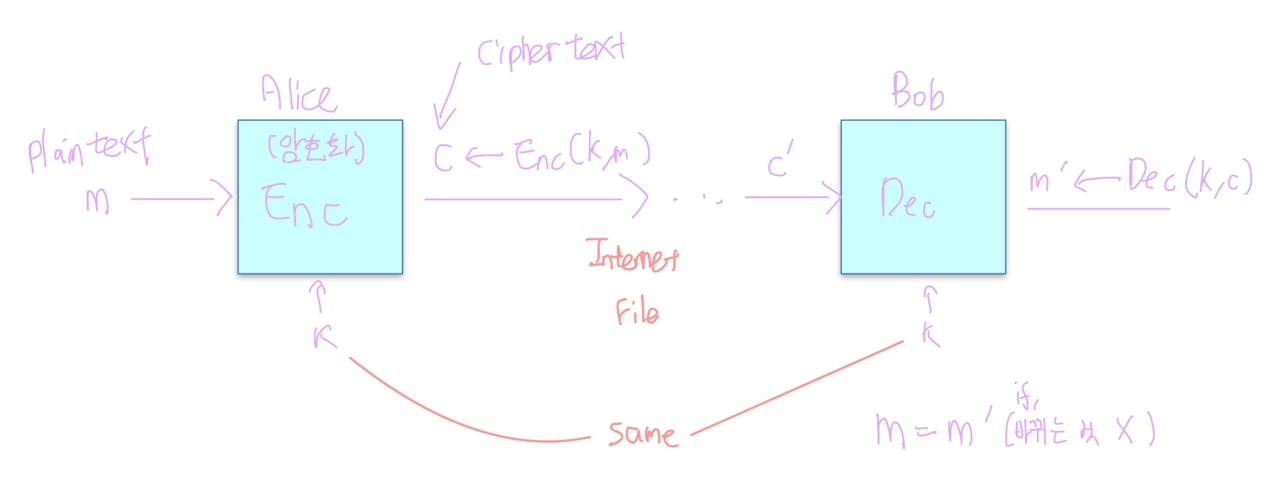
대칭 키 암호: 암호화 알고리즘의 한 종류로, 암호화와 복호화에 같은 암호 키를 쓰는 알고리즘을 의미한다. 대칭 키 암호에서는 암호화를 하는 측과 복호화를 하는 측이 같은 암호 키를 공유해야 한다.

Few Historic Examples

전부 다 깨지긴 함...

1. Substitution cipher

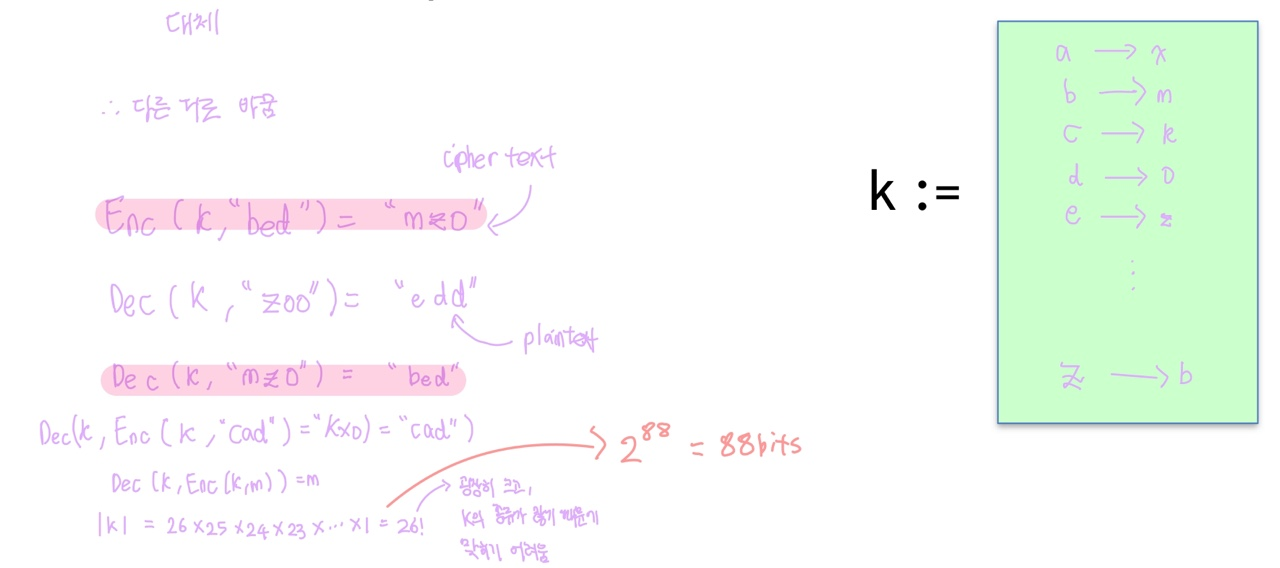
Caesar cipher(카이사르 암호)

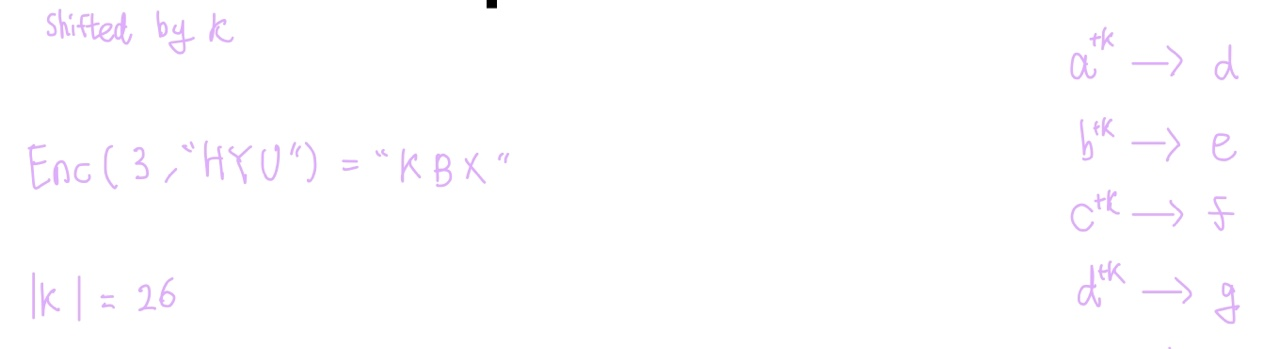
How to break a substitution cipher?

• 가장 많이 쓰이는 영어 알파벳
• 가장 많이 쓰이는 digrams

2. Vigenere cipher (비즈네르 암호)

알파벳의 위치에 따라 시프트 위치가 변함

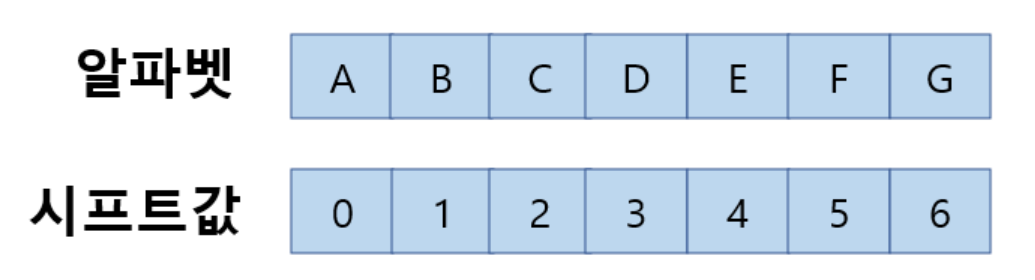
예를 들어, HELLO WORLD를 키값 BAG로 하여 비즈네르 암호를 이용하고 싶은 경우다.

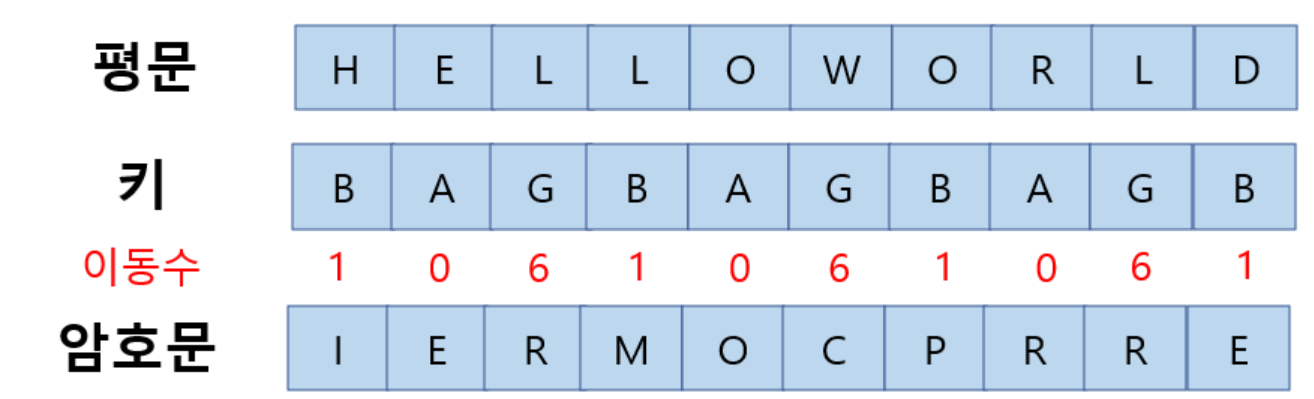
이런 식으로 최종 암호문이 나온다.

Rotor Machines

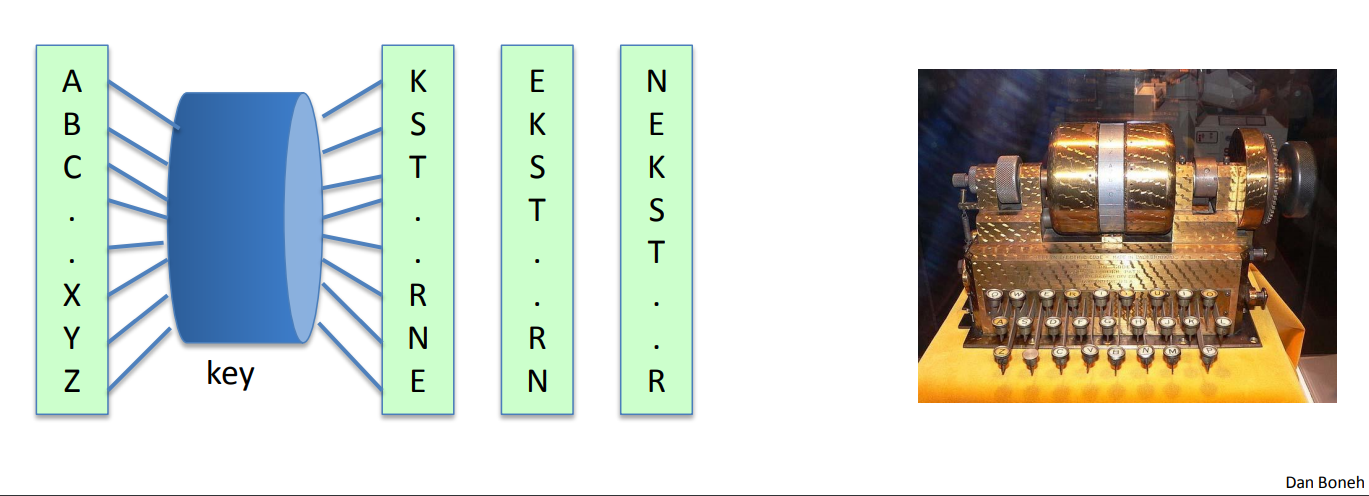
Data Encryption Standard

DES: 안전하지 않음
현재 쓰고 있는 건 아직 공격 반응을 찾지 못해서 안전하다. 찾을 경우에는 새로운 암호를 만들어야 함.

Discrete Probability

시간이 지날수록 암호가 꼭 안전하다는 것은 불가능해졌고, 그래도 안전한 암호를 만들기 위해 여러 가지 정밀하고 세심한 보안 절차를 거친다. 그리고 그러한 보안 절차를 걸칠 때, 사용되는 도구가 바로 ‘이산 확률(Discrete Probability)'임.

U: 유한집합, 0,1의 n비트 짜리다. 그렇기에 만약 0,1의 3비트짜리인 경우 총 8개가 나온다. n개의 bit를 가지면서 각 bit가 2가지의 경우의 수를 갖기 때문에, 집합의 원소의 개수는 2^n다.

P: 확률분포 P(x)의 확률을 더하면 1이 된다.

1. Uniform distribution:

균등 분포는 집합 U에 속한 모든 x가 동일한 P(x) 값을 가지는 경우를 말합니다. {00, 01, 10, 11}의 예시에 따르면 각 원소들이 동일하게 1/4의 확률을 가지는 것이다.

2. Point distribution:

집합 U에 속한 특정 x의 P(x)만 1의 확률을 가지고, 그외 나머지는 모두 0의 확률을 가지는 경우를 말한다. {00, 01, 10, 11}의 예시에 따르면 {10}만 1이고, 나머지는 항상 0의 확률을 갖게되는 경우다.

Distribution Vector: 각각의 확률분포 P(x)를 묶어서 일종의 배열이나 벡터로 표현했다.

Events

사건: 각각의 원소들의 집합
x = 각각의 사건들이 일어날 원소들의 합
P(x): 이벤트가 일어날 확률

Example

• 예를 들어, 0,1의 8비트 총 2의 8승인 256개가 있다. 그리고 맨 마지막 비트 두개가 11인 x들을 모아 사건의 집합을 구한다. 그리고 이것이 전체 집합인 U보다 작거나 같아야 한다.
  그렇게 되면 A의 경우에는..
  • A = {00000011, 00000111, 00001111, ... 11111111}
    2의 8승(전체 경우)분의 2의 6승이다.(뒤에 두 비트만 1) 그렇게 되면 이 사건의 확률은 1/4이 된다.

The union bound

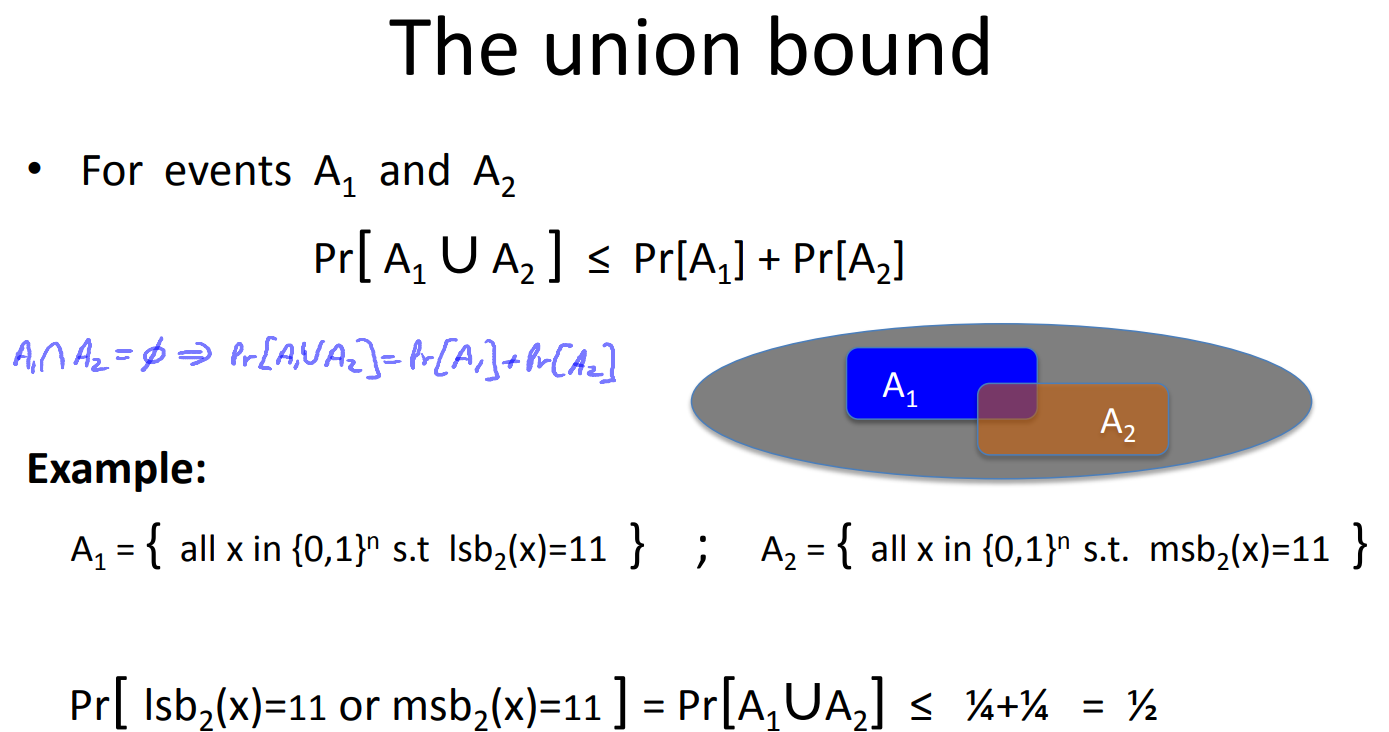
각 이벤트의 확률의 덧셈을 계산하는 것이 아니고 이벤트의 합집합의 확률을 계산한다.

• 왜냐하면 교집합(intersection)이 중복되어 계산된다. 그렇기 때문에 배반사건의 경우(교집합 x)에서는 Pr(A) + Pr(B) = Pr(A U B) 가 성립하고, 보통의 경우 합집합이 더 작으므로 부등호를 사용해 표현하는 것이 일반적이다. 따라서 Pr[lsb2(x) = 11 or msb2(x) = 11] 은 이것을 각각 계산한 1/4 + 1/4 보다 작거나 같다.

Random Variables

확률변수 X란, U -> V로 매핑한다. 랜덤변수는 X(y) = lsb(y)로 끝의 값 0,1만 return한다. 집합 U에서 어떠한 원소든지 무작위로 선택하더라도 V집합의 0 혹은 1에 1/2의 확률만 나오게 된다.

The uniform random variable

균등 확률 변수: Pr[r=a] 의 확률이 모두 1 / |U| 로 같아서, 어떤 확률변수를 갖더라도 모두 같은 값을 가진다.

r이 {0,1}^2인 uniform random variable이고, 이때 X = r1 + r2라면, Pr[X=2]는 무엇인지를 묻는 예제다.
uniform이라고 했으므로, {00, 01, 10, 11} 이 모두 1/4. 이때의 X는 각각 0, 1, 1, 2가 되고 중복원소를 제거하면 {0, 1, 2}가 된다. 확률로는 각각 1/4, 1/2, 1/4 이 되기에, Pr[X=2]는 1/4 이 정답이다.

Randomized algorithms

확률적 알고리즘

• Deterministic algorithm: 예측한 그대로만 적용, 입력값이 m이면그 결과가 항상 동일한 y=A(m)으로만 도출된다.

• Randomized algorithm: m과 함께 r이라는 값이 함께 input으로 작용한다. 값은 수행할 때마다 매번 다르게 생성되므로, 같은 m값을 입력했더라도 매번 다른 y 값이 도출된다.

이것을 암호학적으로 해석하면 m을 암호화할 때 항상 key를 사용한다. 동일한 메세지에서도 항상 다른 결과값만 보여주기에, attack하기 어렵다.