[프로그래머스] 양과 늑대 C++ - DFS

문제

2진 트리 모양 초원의 각 노드에 늑대와 양이 한 마리씩 놓여 있습니다. 이 초원의 루트 노드에서 출발하여 각 노드를 돌아다니며 양을 모으려 합니다. 각 노드를 방문할 때 마다 해당 노드에 있던 양과 늑대가 당신을 따라오게 됩니다. 이때, 늑대는 양을 잡아먹을 기회를 노리고 있으며, 당신이 모은 양의 수보다 늑대의 수가 같거나 더 많아지면 바로 모든 양을 잡아먹어 버립니다. 당신은 중간에 양이 늑대에게 잡아먹히지 않도록 하면서 최대한 많은 수의 양을 모아서 다시 루트 노드로 돌아오려 합니다.
https://programmers.co.kr/learn/courses/30/lessons/92343
👉🏻 예시는 실제 문제를 참고!

[1번 예시]

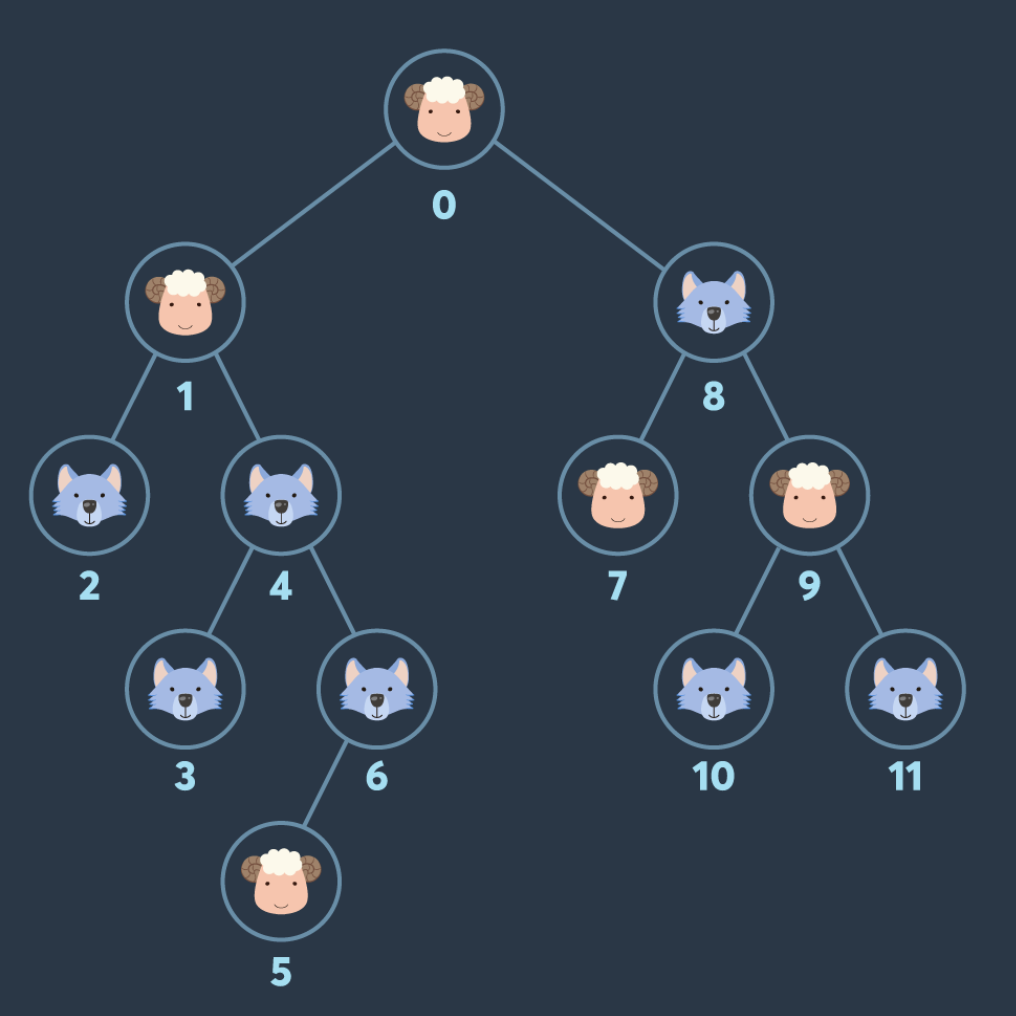
풀이방식

문제를 보고 dfs를 이용한 완전 탐색이라고 생각하고 코드를 작성했고, 이 문제는 방문한 노드를 또 방문할 수 있기에 visit 배열로 check할 필요가 없었지만, 그렇다면 이미 방문한 양 노드를 다시 방문할 때 카운트 추가를 안하는 방식을 생각했다. => 틀린 답이 나왔고, 비효율적이었다.

🎈참고한 풀이방식
앞서 말한 것 처럼, 이 문제는 노드를 재방문 할 수 있다. 여러번 0번 노드부터 다시 시작하는 방법이 아닌 지금 위치에서 갈 수 있는 노드를 중심으로 탐색해야 한다. 즉 1번 예시처럼, 0번 노드에서 처음으로 갈 수 있는 노드는 {1,8}이다. 만약, 0->1번을 방문했다면 갈 수 있는 노드들이 저장된 벡터에는 {8,2,4}가 존재할 것이다. 이러한 방식으로 연결된 노드들을 저장하고 그때 따라오는 양과 늑대의 수를 세어 양의 최대값을 구하면 된다.

코드

#include <string>
#include <vector>
#include <algorithm>
using namespace std;

int answer = 1;
int s = 0;
int w = 0;

void dfs(int curr_idx, int w, int s, vector<int> nextNode, vector<int> info, vector<vector<int>> v) {
    int animal = info[curr_idx];
    if(!animal) s++;
    else w++;
    
    answer = max(answer, s);
    
    if(w >= s) return;
    
    for(int i = 0; i < nextNode.size(); i++) {
        vector<int> next = nextNode;
        next.erase(next.begin()+i);
        for(int j = 0; j < v[nextNode[i]].size(); j++) 
            next.push_back(v[nextNode[i]][j]);
        dfs(nextNode[i],w,s, next, info, v);
    }
}


int solution(vector<int> info, vector<vector<int>> edges) {
   vector<vector<int>> v(info.size());

    for(int i = 0; i < edges.size(); i++) 
        v[edges[i][0]].push_back(edges[i][1]);
    
    vector<int> nextNode; //0번 노드와 연결된 값부터 시작하기 위해서
    for(int i = 0; i < v[0].size(); i++)
        nextNode.push_back(v[0][i]);
    
    dfs(0,0,0,nextNode, info, v);
    
    
    return answer;
}

🧐 회고

갈 수 있는 노드들만 탐색하는 방식을 생각하지 못해 처음에는 너무 어렵게 느껴졌던 것 같다. 다른 사람의 코드를 보니 비트마스킹을 이용하여 푼 경우도 있어서 이참에 비트마스킹도 제대로 공부하고 다시 풀어봐야겠다.!