[BOJ] 백준 2292번 벌집 (Java)

BOJ: Q2292 - 벌집 [ 브론즈 2 ]

문제

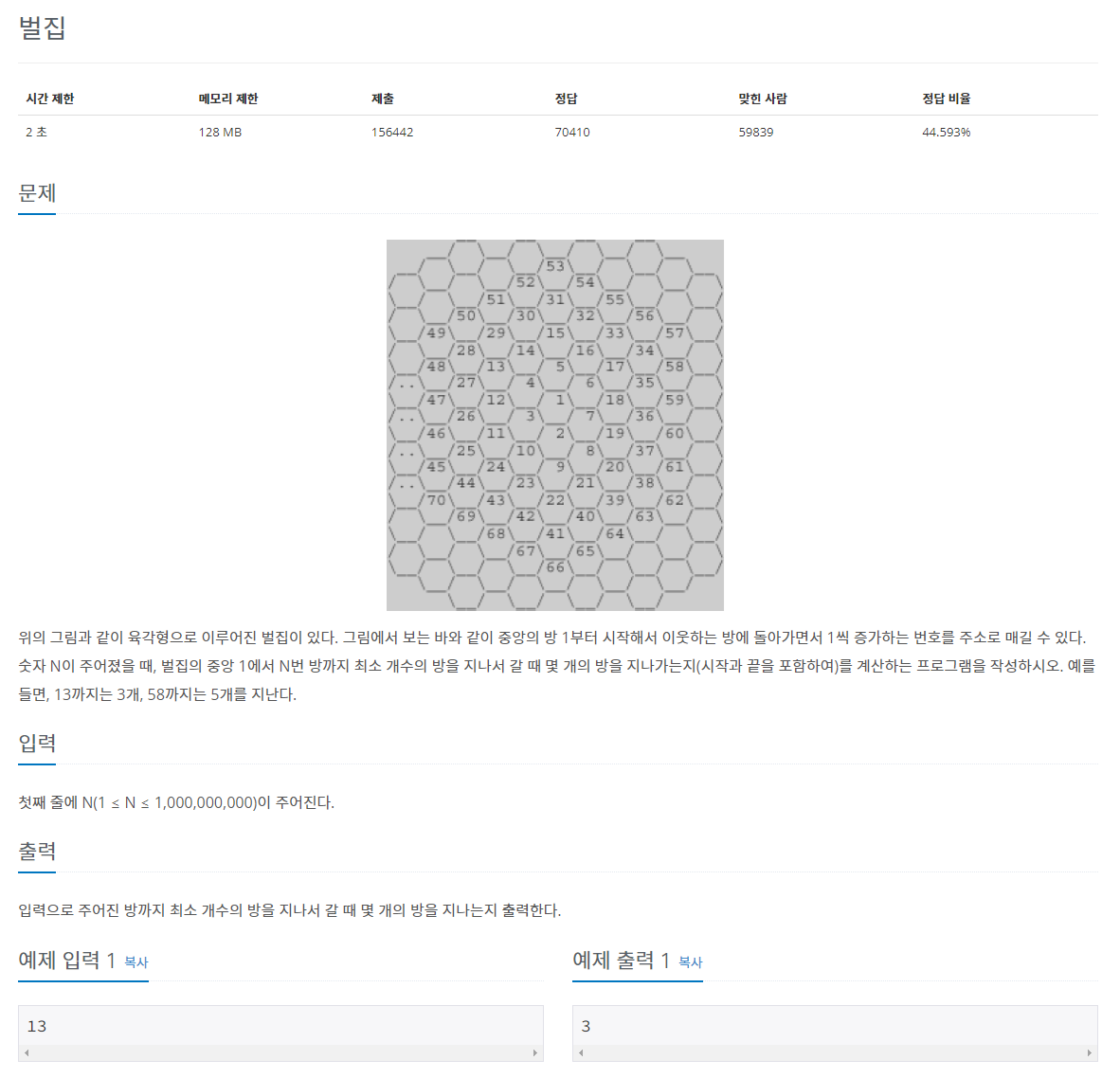
위의 그림과 같이 육각형으로 이루어진 벌집이 있다. 그림에서 보는 바와 같이 중앙의 방 1부터 시작해서 이웃하는 방에 돌아가면서 1씩 증가하는 번호를 주소로 매길 수 있다. 숫자 N이 주어졌을 때, 벌집의 중앙 1에서 N번 방까지 최소 개수의 방을 지나서 갈 때 몇 개의 방을 지나가는지(시작과 끝을 포함하여)를 계산하는 프로그램을 작성하시오. 예를 들면, 13까지는 3개, 58까지는 5개를 지난다.

입력

첫째 줄에 N(1 ≤ N ≤ 1,000,000,000)이 주어진다.

출력

입력으로 주어진 방까지 최소 개수의 방을 지나서 갈 때 몇 개의 방을 지나는지 출력한다.

예제

입력 1

13

출력 1

3

입력 2

58

출력 2

5

풀이

import java.io.*;

public class Q2292 {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));

        int n = Integer.parseInt(br.readLine().trim());

        int cnt = 1;
        int num = 1;
        int addNum = 0;

        while (n > num) {
            addNum += 6;
            num += addNum;
            cnt++;
        }

        bw.write(String.valueOf(cnt));
        bw.flush();
    }
}

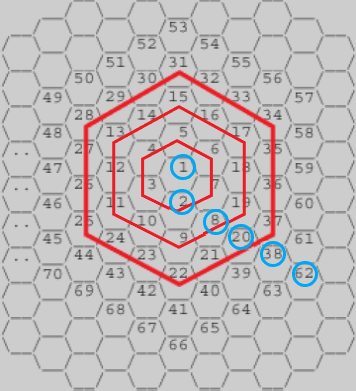
위 사진을 보면, 각 육각형의 숫자 중 육각형의 시작 부분(각 육각형의 숫자 중 가장 작은 수)을 나열하면

2 8 20 38 62

위와 같이 나열된다. 이 수들 사이의 차를 구해보면

2  8  20  38  62
 6  12  18  24

위와 같이 나열되고, 새로 나온 수들의 차를 다시 구하면

2  8  20  38  62
 6  12  18  24
   6   6   6

위처럼 나옵니다.
즉 육각형의 시작 숫자들이 증가하는 차가 6씩 늘어난다는 것인데,
1을 제외한 가장 작은 육각형부터 이루고 있는 숫자들을 확인해보면

1번째 육각형을 이루는 숫자: 2 ~ 7
2번째 육각형을 이루는 숫자: 8 ~ 19
3번째 육각형을 이루는 숫자: 20 ~ 37
4번째 육각형을 이루는 숫자: 38 ~ 61
5번째 육각형을 이루는 숫자: 62 ~ 

위와 같이 이루러져 있고,
1에서 시작하여 n번째 육각형을 이루고 있는 숫자에 도달하려면 n + 1번의 이동이 필요합니다.
따라서 소스에서 cnt는 몇 번 이동하는지 확인하기 위하여 1로 초기화 하였고, while문이 돌 때마다 1씩 증가시킵니다.
0부터 시작하여 while문을 돌 때마다 6씩 늘어나는 addNum을 num에 추가하여 num이 찾을 숫자인 n보다 작은지 확인합니다.
여기서 num은 1에서 시작하여 addNum을 더하기 때문에, 각 육각형에서 가장 큰 수가 됩니다. 따라서 n이 num보다 크다면 더 큰 육각형을 이루는 원소라는 의미가 됩니다.
따라서 이 조건을 while문의 조건으로 넣게 된다면 n이 이루는 육각형이 몇 번째 인지, 그리고 n까지 가는 데 몇 번의 이동이 필요한지 구할 수 있게 됩니다.