
문제
N 개의 막대 기둥이 일렬로 세워져 있다. 기둥들의 폭은 모두 1 m이며 높이는 다를 수 있다. 이 기둥들을 이용하여 양철로 된 창고를 제작하려고 한다. 창고에는 모든 기둥이 들어간다. 이 창고의 지붕을 다음과 같이 만든다.
- 지붕은 수평 부분과 수직 부분으로 구성되며, 모두 연결되어야 한다.
- 지붕의 수평 부분은 반드시 어떤 기둥의 윗면과 닿아야 한다.
- 지붕의 수직 부분은 반드시 어떤 기둥의 옆면과 닿아야 한다.
- 지붕의 가장자리는 땅에 닿아야 한다.
- 비가 올 때 물이 고이지 않도록 지붕의 어떤 부분도 오목하게 들어간 부분이 없어야 한다.
그림 1은 창고를 옆에서 본 모습을 그린 것이다. 이 그림에서 굵은 선으로 표시된 부분이 지붕에 해당되고, 지붕과 땅으로 둘러싸인 다각형이 창고를 옆에서 본 모습이다. 이 다각형을 창고 다각형이라고 하자.
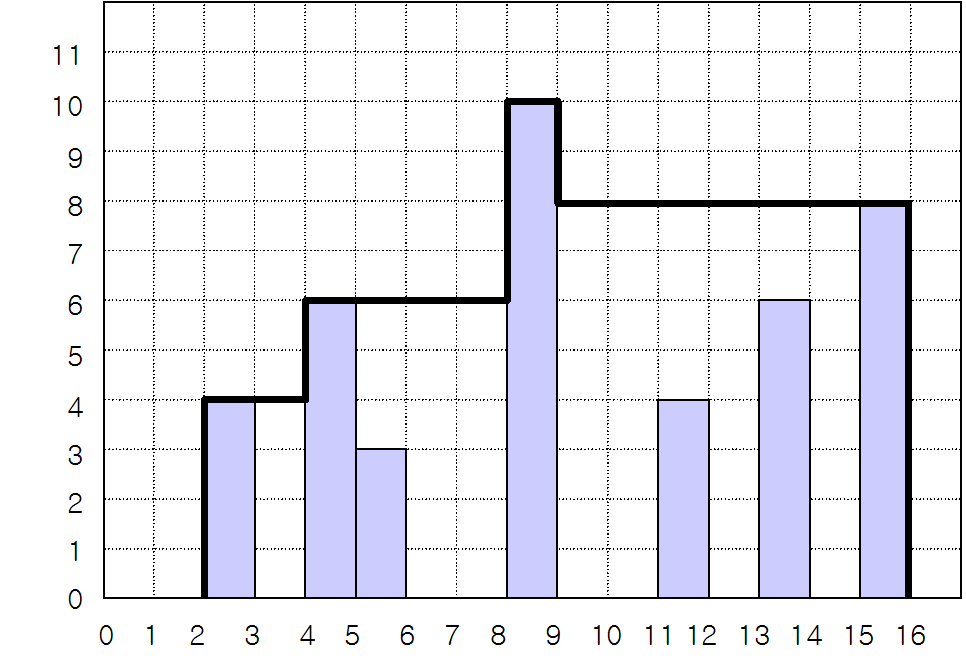
창고 주인은 창고 다각형의 면적이 가장 작은 창고를 만들기를 원한다. 그림 1에서 창고 다각형의 면적은 98 ㎡이고, 이 경우가 가장 작은 창고 다각형이다.
기둥들의 위치와 높이가 주어질 때, 가장 작은 창고 다각형의 면적을 구하는 프로그램을 작성하시오.
입력
- 첫 줄에는 기둥의 개수를 나타내는 정수 N이 주어진다. N은 1 이상 1,000 이하이다.
- 그 다음 N 개의 줄에는 각 줄에 각 기둥의 왼쪽 면의 위치를 나타내는 정수 L과 높이를 나타내는 정수 H가 한 개의 빈 칸을 사이에 두고 주어진다.
- L과 H는 둘 다 1 이상 1,000 이하이다.
출력
- 줄에 창고 다각형의 면적을 나타내는 정수를 출력한다.
예제
입력
7
2 4
11 4
15 8
4 6
5 3
8 10
13 6출력
98풀이
from collections import Counter
N = int(input())
pillar = [list(map(int, input().split())) for _ in range(N)] # 기둥. [위치, 높이]
pillar.sort(key=lambda x: x[0]) # 위치 기준으로 오름차순 정렬
max_height = max(pillar, key=lambda x: x[1])[1] # 가장 큰 기둥 높이
height_count = Counter(list(zip(*pillar))[1]) # 기둥의 높이 별 개수
max_height_num = height_count[max_height] # 가장 큰 높이를 가진 기둥의 개수.
area = 0 # 면적
x, y = pillar[0][0], 0 # 좌표 초기화
for i in range(len(pillar)): # 정렬된 기둥들을 차례로 가져와 반복문 실행
p = pillar[i]
if max_height_num > 0: # 가장 큰 높리를 가진 기둥을 다 지나지 않은 경우. 지붕 상승 또는 유지
if p[1] >= y: # 현재 기둥이 직전 기둥보다 크거나 같은 경우
area += (p[0] - x) * y # 직전 기둥과 현재 기둥 사이의 면적을 구해 area에 더함
x = p[0] # x, y 좌표 최신화
y = p[1]
if p[1] == max_height: # 현재 기둥이 가장 큰 기둥인 경우
area += y # 기둥이 위치한 면적 더함. 위 그림에서는 8~9 사이의 면적
x += 1 # x 좌표 1 증가
max_height_num -= 1 # 가장 큰 기둥을 1 뺀다.
else: # 전체에서 가장 큰 기둥은 지나감.
# 현재 기둥 포함 이후 가장 큰 기둥의 높이를 대입
max_height = max(pillar[i:], key=lambda x: x[1])[1]
if max_height == p[1]: # 현재 기둥이 가장 크다면
y = p[1] # y w 좌표 최신화
area += (p[0] - x + 1) * y # 현재 기둥까지의 면적 더해줌
x = p[0] + 1 # x 좌표 최신화
print(area)가장 큰 기둥을 찾고, 그 기둥을 기준으로 나눠서 면적을 구했다. 가장 큰 기둥과 같은 높이를 가진 기둥이 또 존재할 수 있으므로, 해당 높이를 가진 기둥의 개수를 구하고 그 수가 0이 될 때를 기준으로 삼았다.
기준 이전에는 직전 기둥의 높이를 저장해놓은 후에 현재 기둥이 더 높거나 같다면 면적을 더하는 방식으로 했다. 이 때에는 기둥의 왼쪽 선을 기준으로 면적을 구했다.
가장 큰 기둥(기준)에 도달하게 되면, 해당 기둥이 차지하는 면적(왼쪽 선과 오른쪽 선 사이. 그림에서는 8~9 사이)를 더해준다.
기준 이후에는 남은 기둥들 중 가장 큰 기둥의 높이를 구한다. 그리고 현재 기둥의 높이가 해당 높이를 가지는지 확인하고, 그렇다 하면 현재 직전 기둥에서 현재 기둥까디 면적을 구해서 더한다. 이 때에는 오른쪽 선이 기중이 된다.
