
Tree
트리란 스택이나 큐와 같은 선형 구조가 아닌 비선형 구조이고 계층적 관계(Hierachical Relationship)을 표현하는 자료구조이다.
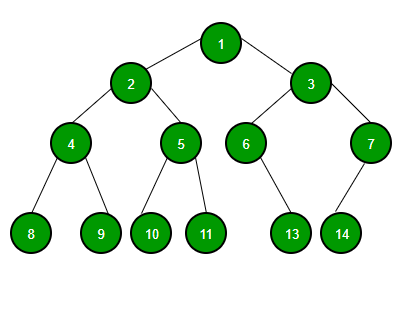
구성 요소
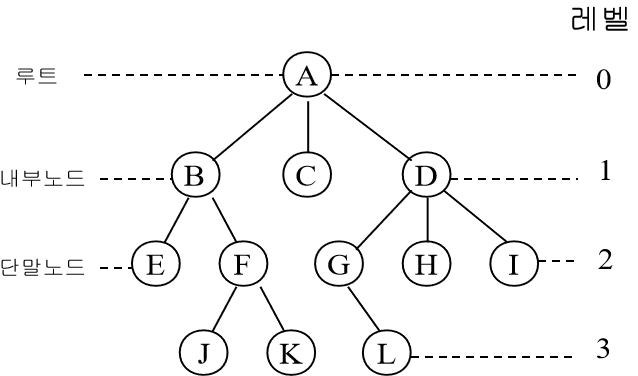
- Node(노드): 트리를 구성하고 있는 각각의 요소
- Edge(간선): 트리에서 노드와 노드 사이를 연결하는 선
- Root Node(루트 노드): 트리 구조에서 최상단에 위치한 노드. 부모가 없는 노드
- Termanal Node(Leaf Node, 단말 노드): 하위에 더이상 다른 노드가 연결되어 있지 않은 노드. 자식이 없는 노드
- Internal Node(내부 노드, 비단말 노드): 단말 노드를 제외한 모든 노드. 루트 노드도 포함.
- 레벨(level, 깊이(depth)): 루트에서 어떤 노드까지의 경로 길이(간선의 수)
- 트리의 높이(height): 트리의 최고 레벨
- 부모 노드: 자신과 연결된 상위 노드
- 자식 노드: 자신과 연결된 하위 노드
- 형제 노드: 같은 부모를 가지는 노드
- 크기(size): 특정 노드가 자신을 포함한 자손의 수
- 노드의 차수(degree): 노드가 가진 자식 노드의 수
- 트리의 차수(degree): 노드의 차수 중 최댓값
특징
- 트리에는 사이클이 존재하지 않는다.
사이클이 존재한다면, 그것은 트리가 아닌 그래프이다. - 루트에서 어떤 한 노드로 가는 경로는 유일하다.
- 노드의 개수가 N개이면 간선의 개수는 N-1개이다.
트리 순회 방식
트리 순회 방식은 총 4가지이다.
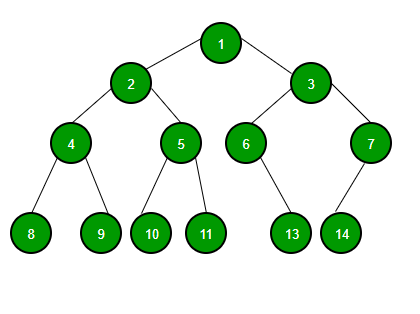
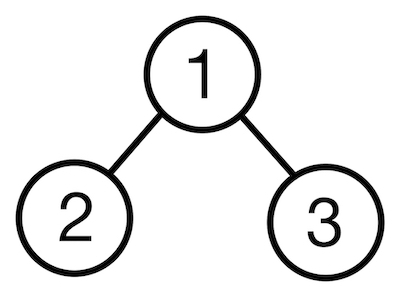
1. 전위 순회 (pre-order)
루트 노드 먼저 방문하는 순회 방법이다.
트리에서 루트에서 시작하여 루트 노드 -> 왼쪽 하위 트리 -> 오른쪽 하위 트리 순서로 순회하는 방법이다.
위의 높이가 2인 트리를 예를 들면 1 -> 2 -> 3 이다.
초록색 노드를 가진 높이가 4인 트리를 전위 순회하면 순서는 아래와 같다.
1 -> 2 -> 4-> 8 -> 9 -> 5 -> 10 -> 11 -> 3 -> 6 -> 13 -> 7 -> 14
2. 중위 순회 (in-order)
왼쪽 하위 트리를 먼저 방문 후 루트 노드, 오른쪽 하위 트리를 방문하는 순회 방법이다.
트리에서 루트에서 시작하여 왼쪽 하위 트리 -> 루트 노드 -> 오른쪽 하위 트리 순서로 순회하는 방법이다.
위의 높이가 2인 트리를 예를 들면 2 -> 1 -> 3이다.
초록색 노드를 가진 높이가 4인 트리를 중위 순회하면 순서는 아래와 같다.
8 -> 4 -> 9 -> 2 -> 5 -> 10 -> 11 -> 1 -> 6 -> 13 -> 3 -> 7 -> 14
3. 후위 순회 (post-order)
왼쪽부터 하위 트리들을 먼저 모두 방문 후 루트 노드를 방문하는 순회 방법이다.
트리에서 루트에서 시작하여 왼쪽 하위 트리 -> 오른쪽 하위 트리 -> 루트 노드 순서로 순회하는 방법이다.
위의 높이가 2인 트리를 예를 들면 2 -> 3 -> 1이다.
초록색 노드를 가진 높이가 4인 트리를 중위 순회하면 순서는 아래와 같다.
8 -> 9 -> 4 -> 10 -> 11 -> 5 -> 2 -> 13 -> 6 -> 14 -> 7 -> 3 -> 1
4. 레벨 순회 (level-order)
루트 노드부터 계층별로 방문하는 방법이다.
위의 높이가 2인 트리를 예를 들면 1 -> 2 -> 3이다.
초록색 노드를 가진 높이가 4인 트리를 중위 순회하면 순서는 아래와 같다.
1 -> 2 -> 3 -> 4 -> 5 -> 6 -> 7 -> 8 -> 9 -> 10 -> 11 -> 13 -> 14
트리 종류
Binary Tree (이진 트리)
모든 노드의 차수가 2 이하인 트리를 말한다.
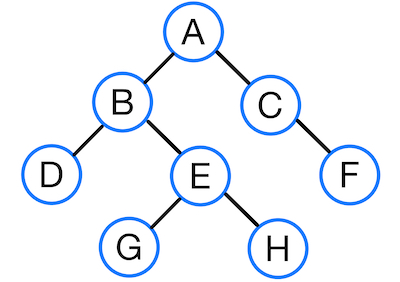
기본적으로 위와 같은 형태를 띈다. 이진 트리도 형태에 따라 다양한 이진트리가 존재한다.
Perfect Binary Tree (포화 이진 트리)
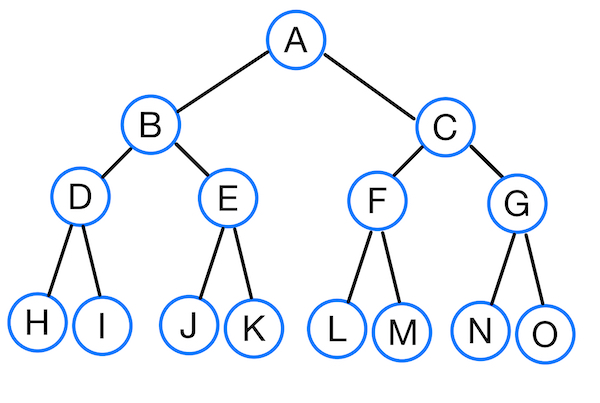
위 그림과 같이 모든 레벨이 꽉 찬 이진 트리를 포화 이진 트리하고 한다.
Complete Binary Tree (완전 이진 트리)
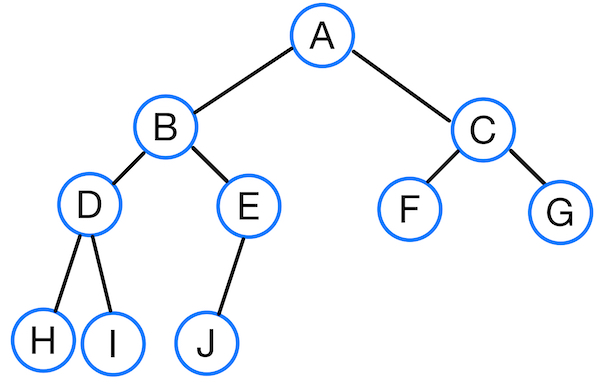
위 그림과 같이 단말노드를 제외한 모든 노드가 위에서 아래로, 왼쪽에서 오른쪽으로 차곡차곡 채워진 이진트리를 완전 이진 트리라고 한다.
Full Binary Tree (정 이진 트리)
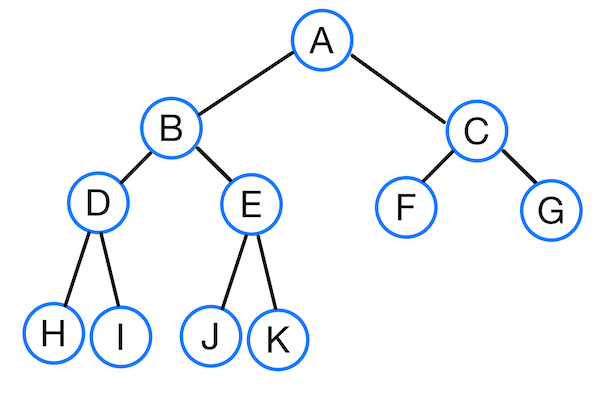
위 그림과 같이 모든 노드가 0개 또는 2개의 자식 노드만을 가지고 있는 트리를 정 이진 트리라고 한다.
배열에서의 이진 트리
배열에서 이진트리의 노드 개수가 n개이고 루트 노드가 1에서 시작할 때, i번째 노드에 대해 부모 노드, 자식 노드의 index는 아래와 같다.parent(i) = i / 2 left_child(i) = 2i right_child(i) = 2i+1
BST (Binary Search Tree, 이진 탐색 트리)
효율적으로 탐색이 가능하고, 이를 위해 효율적으로 저장하는 방법을 고안한 자료구조이다.
이진 탐색 트리는 이진 트리의 한 종류이고, 데이터를 저장하는 규칙이 있다.
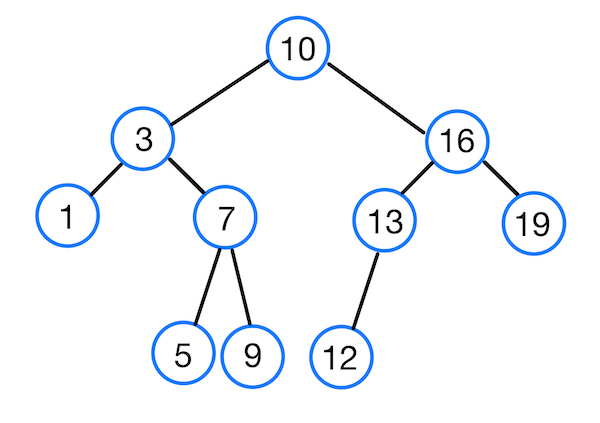
규칙
- 이진 탐색 트리의 노드에 저장된 키는 유일하다.
- 부모의 키가 왼쪽 노드의 키보다 크다.
- 무보의 키가 오른쪽 자식의 키보다 작다.
- 왼쪽과 오른쪽 서브 트리도 이진 탐색 트리이다.
- 중복된 노드는 없다.
중복이 없는 이유?
중복이 많은 경우에 트리를 사용하여 검색 속도를 느리게 할 필요가 없다.
트리에 삽입하는 것보다 노드에 count 값을 가지게 하여 처리하는 것이 효율적이다
시간 복잡도
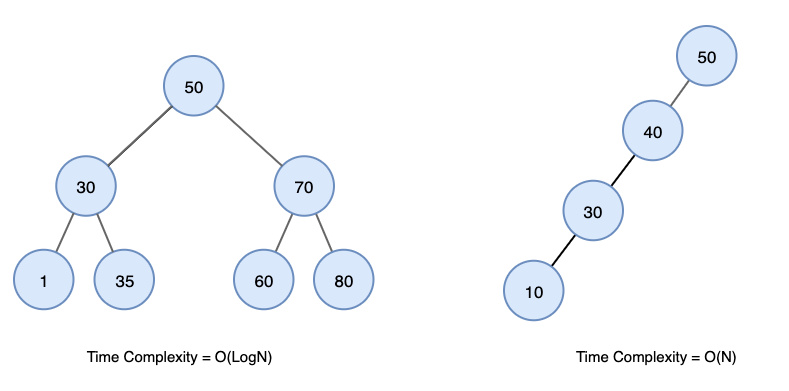
- 균등 트리:
Big-O(log n) - 편향 트리:
Big-O(n)
편향 트리
데이터를 계속 추가하다 보면 지속적으로 한쪽으로만 노드가 추가될 수 있다. 이러면 데이터가 한쪽으로만 몰리는 편향트리가 된다. 이 경우에 균형을 잡기 위한 재조정(Rebalacing)을 수행해야 한다. 이 기법을 구현한 트리 중 하나가Red-Black Tree이다.
생성 예시
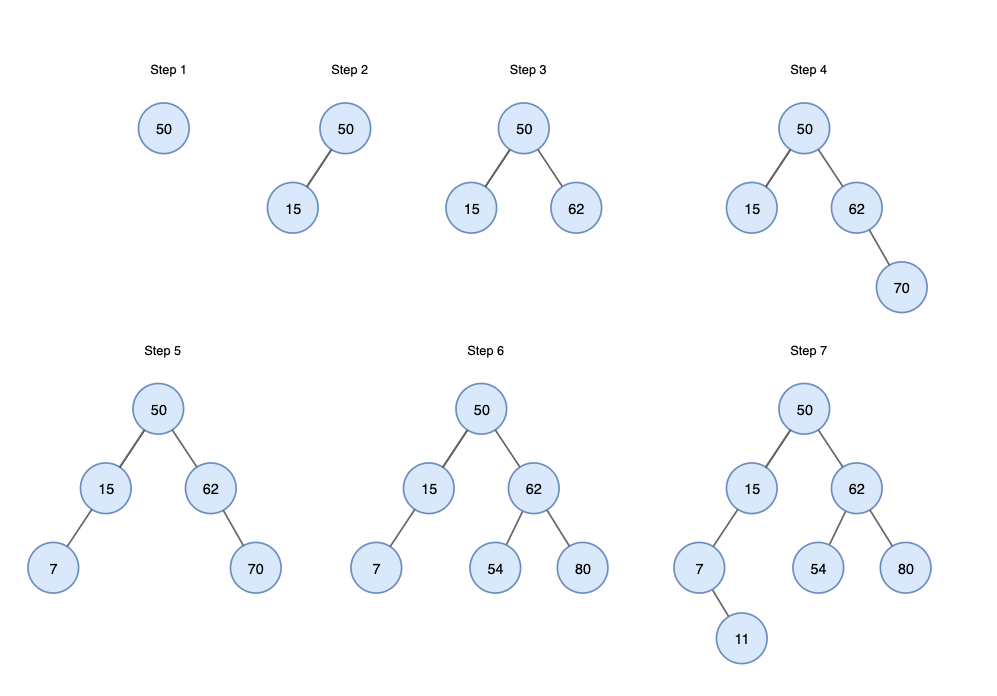
50, 15, 62, 70, 7, 54, 11
위의 숫자를 순서대로 이진 검색 트리에 삽입하면 아래와 같은 순서로 수행된다.
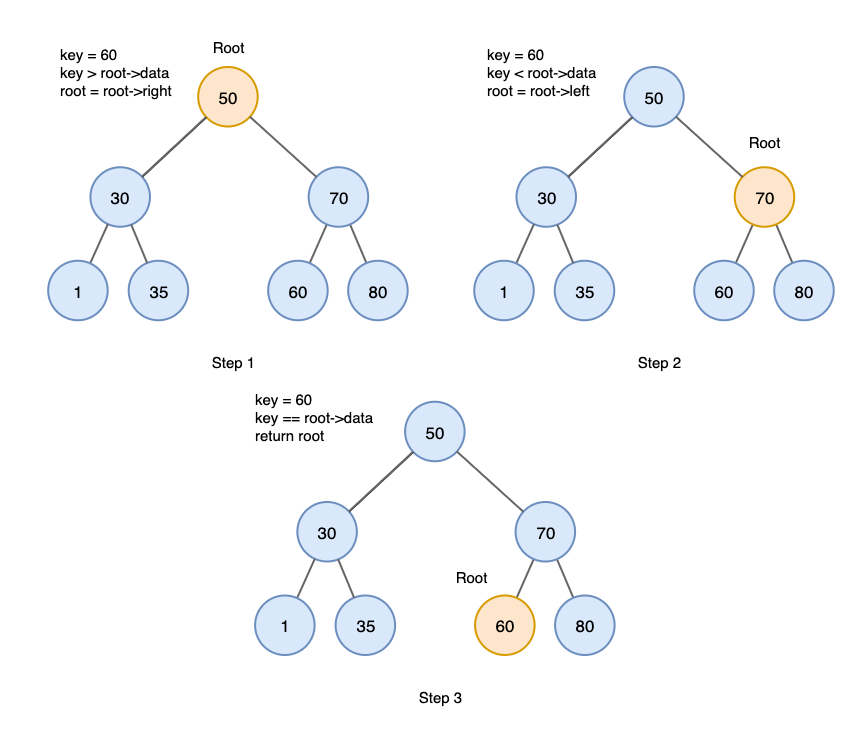
검색 (Serach)
- 루트에서 시작합니다.
- 검색값을 루트와 비교, 루트보다 작으면 왼쪽 자식트리로, 크다면 오른쪽 자식트리로 이동니다.
- 이동한 자식 트리에 대해 2번을 반복합니다.
- 원하는 값을 찾지 못하면 null을 반환합니다.
삽입 (insert)
- 루트에서 시작합니다.
- 삽입값을 루트와 비교, 루트보다 작으면 왼쪽 자식트리로, 크다면 오른쪽 자식트리로 이동니다.
- 이동한 자식 트리에 대해 2번을 반복합니다.
- 리프 노드에 도달한 후 노드보다 작으면 왼쪽, 크면 오른쪽에 삽입합니다.
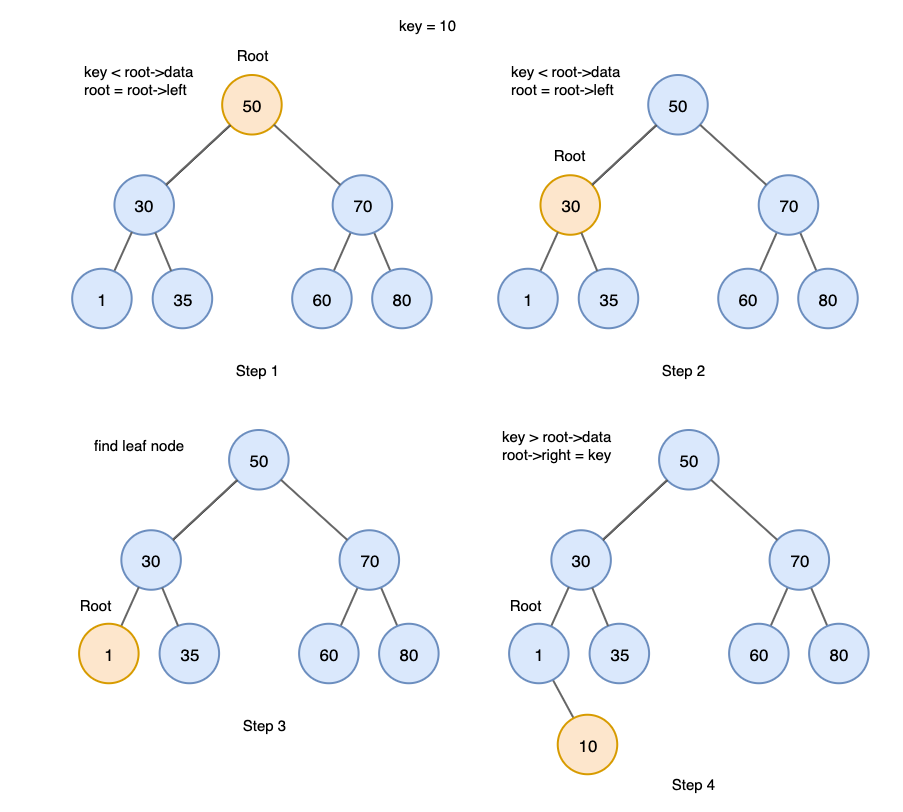
삭제 (delete)
삭제는 3가지의 경우로 나누어 수행합니다.
1. 삭제할 노드가 리프 노드일 경우
- 이 경우에는 그냥 삭제합니다.
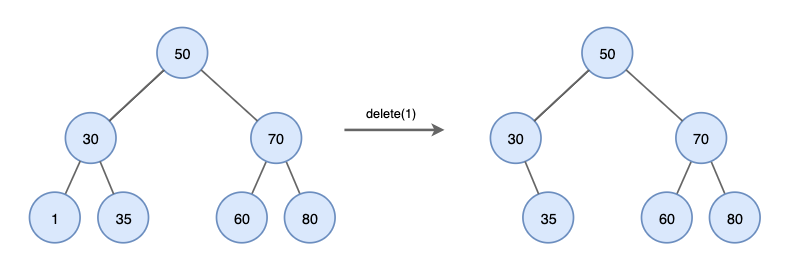
2. 삭제할 노드에 자식이 하나만 있는 경우
- 삭제한 노드를 삭제하고, 자식 노드는 삭제된 노드의 무보 노드에 직접 연결합니다.
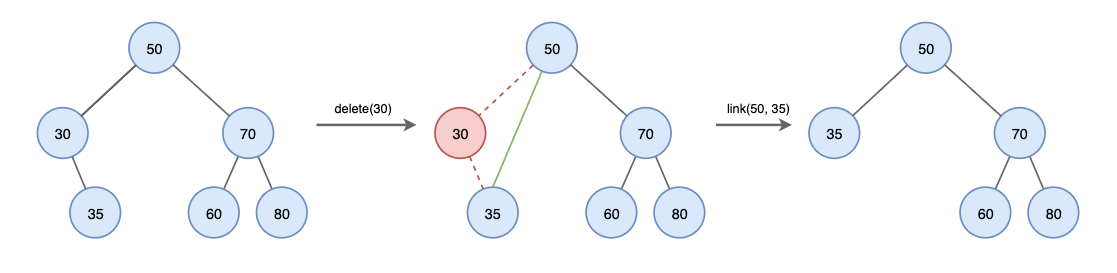
3. 삭제할 노드에 자식이 둘 있는 경우
- 오른쪽 서브 트리에서 가장 작은 값 또는 왼쪽 서브 트리에서 가장 큰 값을 삭제할 노드 자리로 올립니다.
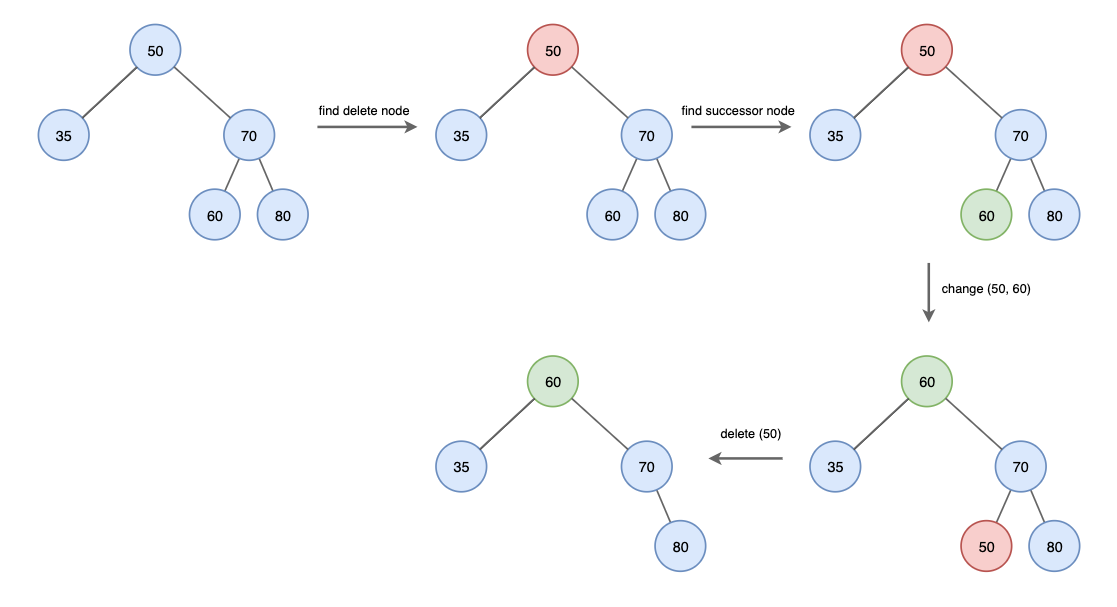
참고
한재엽님 Github Interview_Question_for_Beginner
gyoogle님 Github tech-interview-for-developer
http://www.ktword.co.kr/test/view/view.php?no=4726
https://yoongrammer.tistory.com/71
