정렬

정렬 알고리즘의 정의

정렬 알고리즘	정의
버블(bubble)	데이터의 인접 요소끼리 비교하고, swap 연산을 수행하며 정렬하는 방식
선택(selection)	대상에서 가장 크거나 작은 데이터를 찾아가 선택을 반복하면서 정렬하는 방식
삽입(insertion)	대상을 선택해 정렬된 영역에서 선택 데이터의 적절한 위치를 찾아 삽입하면서 정렬하는 방식
퀵(quick)	pivot 값을 선정해 해당 값을 기준으로 정렬하는 방식
병합(merge)	이미 정렬된 부분 집합들을 효율적으로 병합해 전체를 정렬하는 방식
기수(radix)	데이터의 자릿수를 바탕으로 비교해 데이터를 정렬하는 방식

---

버블 정렬

버블 정렬의 핵심 이론

• 버블 정렬은 두 인접한 데이터의 크기를 비교해 정렬하는 방법
• 간단하게 구현할 순 있지만 ,시간 복잡도는 O(n^2)으로 다른 정렬 알고리즘보다 속도가 느린 편
• 다음 그림과 같이 루프를 돌면서 인접한 데이터 간의 swap 연산으로 정렬

💡 버블 정렬 과정

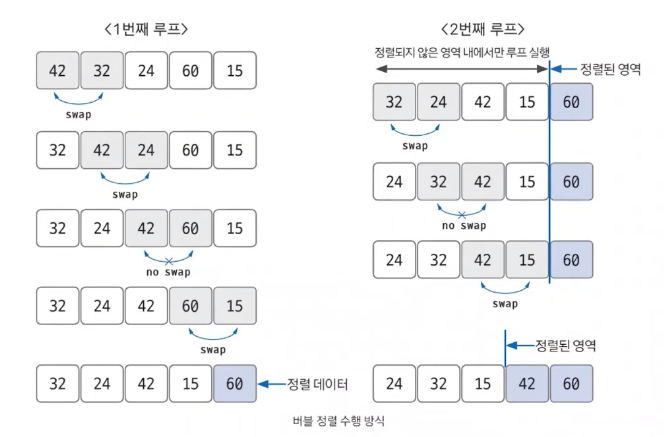
1. 비교 연산이 필요한 루프 범위를 설정
2. 인접한 데이터 값을 비교
3. swap 조건에 부합하면 swap 연산을 수행
4. 루프 범위가 끝날 때까지 2~3을 반복
5. 정렬 영역을 설정. 다음 루프를 실행할 때는 이 영역을 제외
6. 비교 대상이 없을 때까지 1~5를 반복

만약 특정한 루프의 전체 영역에서 swap이 한 번도 발생하지 않았다면 그 영역 뒤에 있는 데이터가 모두 정렬되었다는 뜻이기 때문에 프로세스를 종료해도 된다.

→ 더 이상 정렬 수행 x

---

선택 정렬

• 선택 정렬은 대상 데이터에서 최대나 최소 데이터를 데이터가 나열된 순으로 찾아가며 선택하는 방법
• 구현 방법이 복잡하고, 시간 복잡도도 O(n^2)으로 효율적이지 않아 코딩 테스트에서는 많이 사용하지 않음

선택 정렬의 핵심 이론

• 최솟값 또는 최댓값을 찾고, 남은 정렬 부분의 가장 앞에 있는 데이터와 swap하는 것이 선택 정렬의 핵심

💡 선택 정렬 과정

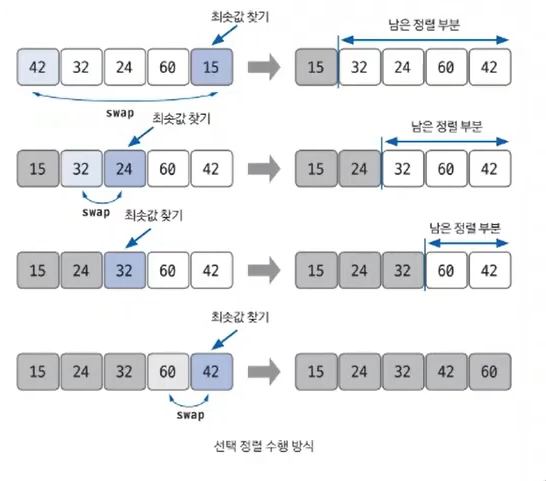
1. 남은 정렬 부분(정렬해야 하는 부분)에서 최솟값 또는 최댓값을 탐색
2. 남은 정렬 부분에서 가장 앞에 있는 데이터와 선택된 데이터를 swap
3. 가장 앞에 있는 데이터의 위치를 변경해(index++) 남은 정렬 부분의 범위를 축소
4. 전체 데이터 크기만큼 index가 커질 때까지, 즉, 남은 정렬 부분이 없을 때까지 반복

---

삽입 정렬

• 삽입 정렬은 이미 정렬된 데이터 범위에 정렬되지 않은 데이터를 적절한 위치에 삽입시켜 정렬하는 방식
• 시간 복잡도는 O(n^2)으로 느린 편이지만 구현하기가 쉽다.
• 코딩 테스트에서 많이 사용하지는 않음

삽입 정렬의 핵심 이론

• 선택 데이터를 현재 정렬된 데이터 범위 내에서 적절한 위치에 삽입하는 것

💡 삽입 정렬 과정

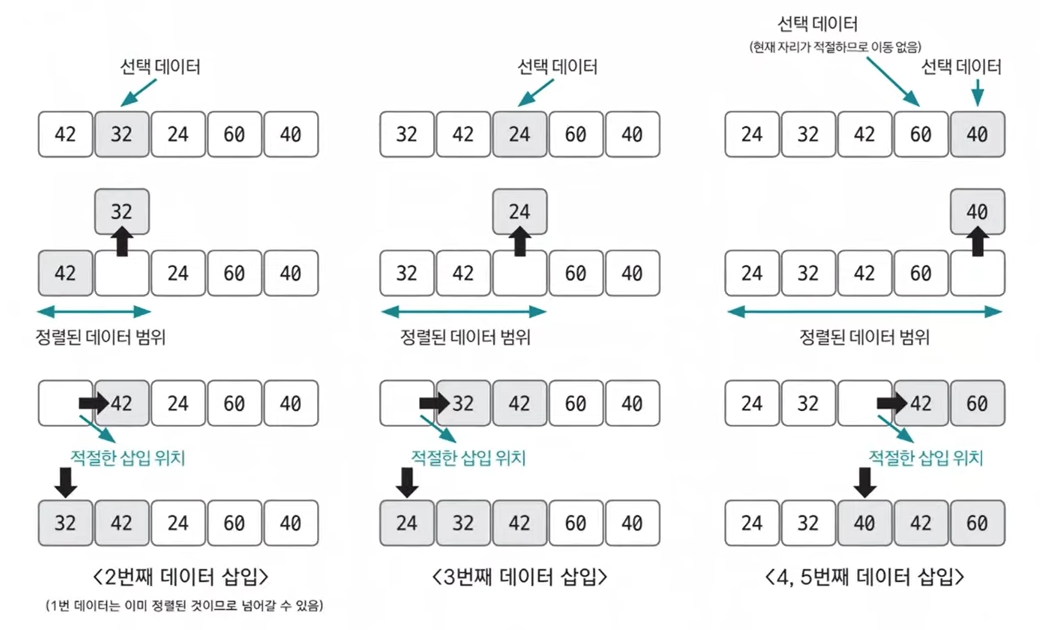
1. 현재 index에 있는 데이터 값을 선택
2. 현재 선택한 데이터가 정렬된 데이터 범위에 삽입될 위치를 탐색
3. 삽입 위치부터 index에 있는 위치까지 shift 연산을 수행
4. 삽입 위치에 현재 선택한 데이터를 삽입하고 index++ 연산을 수행
5. 전체 데이터의 크기만큼 index가 커질 때까지, 즉 선택할 데이터가 없을 때까지 반복

적절한 삽입 위치를 탐색하는 부분에서 이진 탐색 등과 같은 탐색 알고리즘을 사용하면 시간 복잡도를 줄일 수 있다. : O(n) → O(logn)

---

퀵 정렬

• 퀵 정렬은 기준값(pivot)을 선정해 해당 값보다 작은 데이터와 큰 데이터로 분류하는 것을 반복해 정렬하는 알고리즘
• 기준값이 어떻게 선정되는지가 시간 복잡도에 많은 영향을 미치고, 평균 시간 복잡도는 O(nlogn)[ex. 병합정렬]이며 최악의 경우는 시간 복잡도가 O(n^2)[ex.버블, 선택, 삽입]이 된다.

퀵 정렬의 핵심 이론

• pivot을 중심으로 계속 데이터를 2개의 집합으로 나누면서 정렬하는 것

💡 퀵 정렬 과정

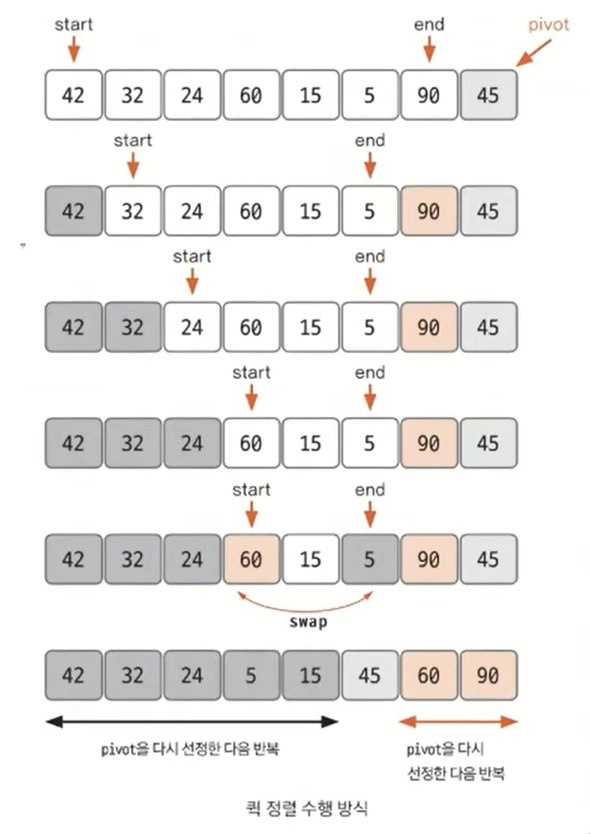
1. 데이터를 분할하는 pivot을 설정(위 그림의 경우 가장 오른쪽 끝을 pivot으로 설정)
2. pivot을 기준으로 다음 a~e과정을 거쳐 데이터를 2개의 집합으로 분리
   1. start가 가리키는 데이터가 pivot이 가리키는 데이터보다 작으면 start를 오른쪽으로 1칸 이동
   2. end가 가리키는 데이터가 pivot이 가리키는 데이터보다 크면 end를 왼쪽으로 1칸 이동
   3. start가 가리키는 데이터가 pivot이 데이터보다 크고, end가 가리키는 데이터가 pivot이 가리키는 데이터보다 작으면 start, end가 가리키는 데이터를 swap하고 start는 오른쪽, end는 왼쪽으로 1칸씩 이동
   4. start와 end가 만날 때까지 a~c를 반복
   5. start와 end가 만나면 만난 지점에서 가리키는 데이터와 pivot이 가리키는 데이터를 비교하여 pivot이 가리키는 데이터가 크면 만난 지점의 오른쪽에, 작으면 만난 지점의 왼쪽에 pivot이 가리키는 데이터를 삽입
3. 분리 집합에서 각각 다시 pivot을 선정
4. 분리 집합이 1개 이하가 될 때까지 과정 1~3을 반복

---

병합 정렬

• 병합 정렬은 분할 정복 방식을 사용해 데이터를 분할하고 분할한 집합을 정렬하여 합치는 알고리즘
• 시간 복잡도는 O(nlogn)
• 코테에 많이 나옴

병합 정렬의 핵심 이론

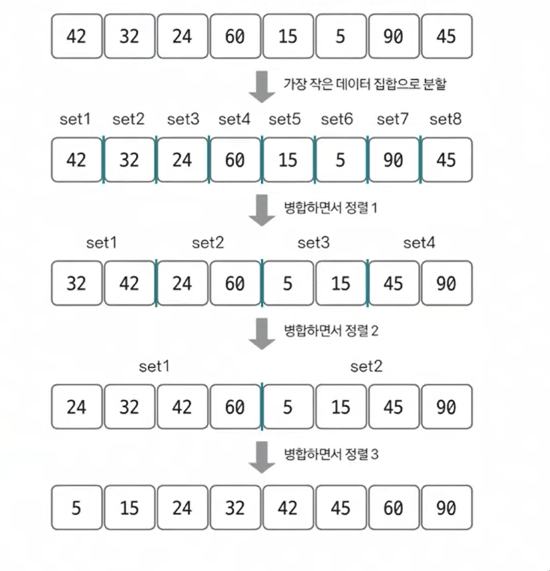
최초에는 8개의 그룹으로 나눈다.(set 1,2…) 이 상태에서 2개씩 그룹을 합치며 오름차순으로 정렬

이어서 2개씩 그룹을 합치며 다시 오름차순 정렬

이어서 그룹을 합치며 오름차순 정렬

• 병합 정렬은 코딩 테스트의 정렬 관련 문제에서 자주 등장
• 특히, 2개의 그룹을 병합하는 원리는 꼭 숙지해야함!

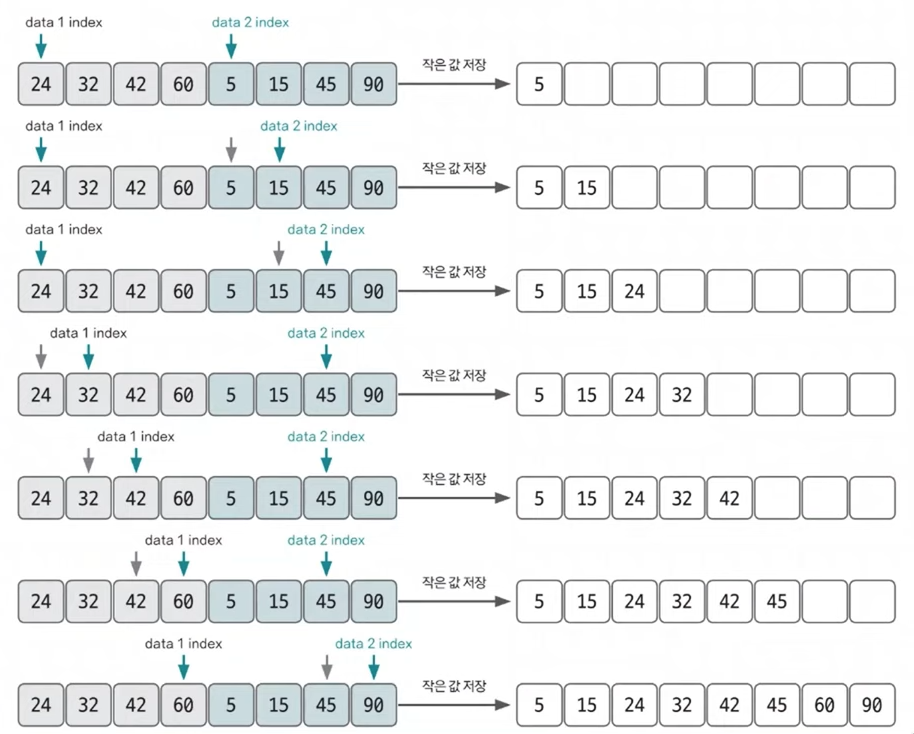
2개의 그룹을 병합하는 과정

• 투 포인터 개념을 사용하여 왼쪽, 오른쪽 그룹을 병합
• 왼쪽 포인터와 오른쪽 포인터의 값을 비교하여 작은 값을 결과 배열에 추가하고 포인터를 오른쪽으로 1칸 이동

---

기수 정렬

• 기수 정렬은 값을 비교하지 않는 특이한 정렬
• 기수 정열은 값을 놓고 비교할 자릿수를 정한 다음 해당 자릿수만 비교
• 시간 복잡도는 O(kn)으로, 여기서 k는 데이터의 자릿수를 뜻함

기수 정렬의 핵심 이론

• 기수 정렬은 10개의 큐를 이용
• 각 큐는 값의 자릿수를 대표

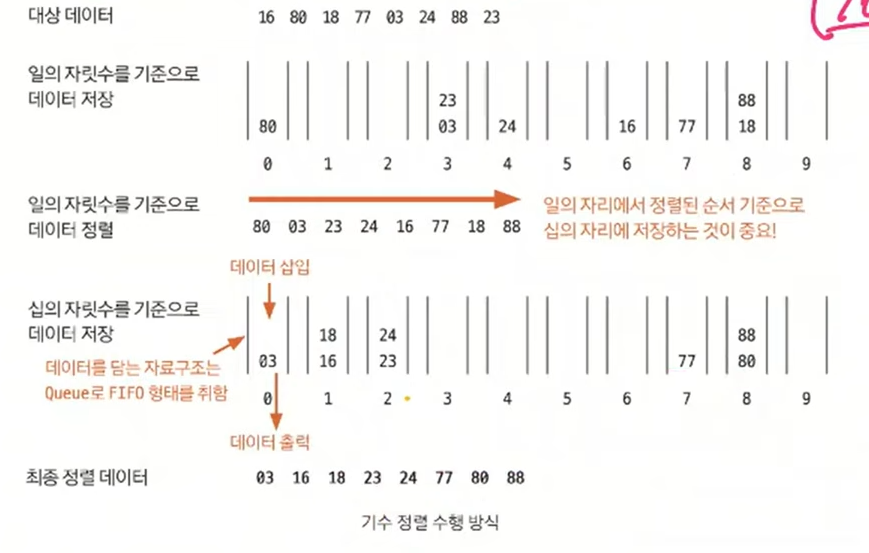
1. 일의 자릿수 기준으로 배열 원소를 큐에 집어 넣음
2. 0번째 큐부터 9번째 큐까지 pop을 진행
3. 이어서 십의 자릿수를 기준으로 같은 과정을 진행
4. 마지막 자릿수를 기준으로 정렬할 때까지 앞의 과정을 반복

• 기수 정렬은 시간 복잡도가 가장 짧은 정렬
• 만약 코딩 테스트에서 정렬해야 하는 데이터의 개수가 너무 많으면 기수 정렬 알고리즘을 활용하자!

---

출처 - 하루코딩