정수론

소수구하기

• 소수는 자신보다 작은 2개의 자연수를 곱해 만들 수 없는 1보다 큰 자연수를 말한다.
• 이와 같은 의미로 1과 자기 자신 외의 약수가 존재하지 않는 수를 말하기도 한다.
• 코딩 테스트에서는 이러한 소수를 판별하는 방식을 묻는 소수 구하기 문제가 종종 출제된다.

소수 구하기의 핵심 이론

• 소수를 구하는 대표적인 판별법으로는 에라토스테네스의 체를 들 수 있다.

🌸 에라토스테네스의 체 원리

1. 구하고자 하는 소수의 범위만큼 1차원 배열을 생성한다.
2. 2부터 시작하고 현재 숫자가 지워지지 않을 때는 현재 선택된 숫자의 배수에 해당하는 수를 배열에서 끝까지 탐색하면서 지운다. 이 때, 처음으로 선택된 숫자는 지우지 않는다.(소수니까)
3. 배열의 끝까지 2를 반복한 후 배열에서 남아 있는 모든 수를 출력한다.

---

오일러 피

• 오일러 피 함수 P[N]의 정의는 1부터 N까지 범위에서 N과 서로서인 자연수의 개수를 뜻한다.
• 서로소는 공약수가 1외에 없는 수

오일러 피의 핵심 이론

• 오일러 피 함수의 원리는 에라토스테네스의 체와 비슷하다.

🌸 오일러 피 함수의 원리

1. 구하고자 하는 오일러 피의 범위만큼 배열을 자기 자신의 인덱스값으로 초기화한다.
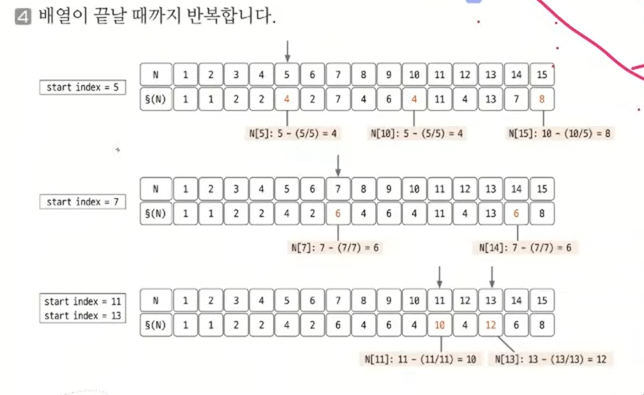
2. 2부터 시작해 현재 배열의 값과 인덱스가 같으면(=소수일 때) 현재 선택된 숫자(K)의 배수에 해당하는 수를 배열의 끝까지 탐색하며 P[i] = P[i] - P[i]/K 연산을 수행한다(i는 K의 배수).
3. 배열의 끝까지 2를 반복하여 오일러 피 함수를 완성한다.

오일러 피 함수의 원리 이해하기

---

유클리드 호제법

• 유클리드 호제법은 두 수의 최대공약수를 구하는 알고리즘이다.

유클리드 호제법의 핵심 이론

• 유클리드 호제법을 수행하려면 먼저 MOD 연산을 이해하고 있어야 한다.
• MOD 연산이 최대 공약수를 구하는 핵심 연산이다.

• MOD 연산을 이해하면 다음과 같이 3단계로 유클리드 호제법을 구현할 수 있다.

🌸 MOD 연산으로 구현하는 유클리드 호제법

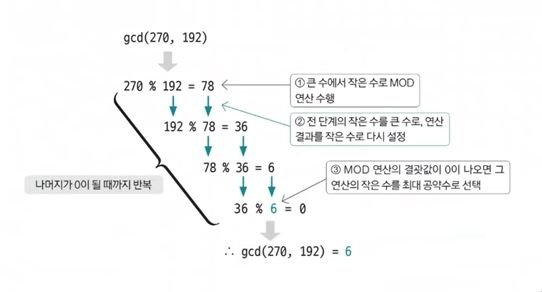
1. 큰 수를 작은 수로 나누는 MOD 연산을 수행한다.
2. 앞 단계에서의 작은 수와 MOD 연산 결괏값(나머지)으로 MOD 연산을 수행한다.
3. 단계2를 반복하다가 나머지가 0이 되는 순간의 작은 수를 최대 공약수로 선택한다.

유클리드 호제법의 원리 이해하기

ex) 270과 192의 최대 공약수 구하기

---

출처 - 하루코딩