조합
- 조합은 그 자체로 코딩 테스트에 자주 출제되는 주제
- 동적 계획법을 이해하는데 기초가 되므로 매우 중요하다.
조합
- 조합은 nCr로 표현하고, 이는 n개의 숫자에서 r개를 뽑는
경우의 수를 뜻한다. - 조합과 비교되는 순열은 nPr로 표현되고, n개의 숫자 중 r개를 뽑아 순서를 고려해 나열할 경우의 수를 뜻한다.
- 순열과 조합의 차이는
순서의 고려 유무이다. - 조합에서는 데이터 1,2,3과 3,2,1을 같은 경우로 판단하고, 순열은 다른 경우로 판단한다.
순열과 조합의 핵심 이론
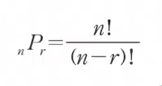
- 순열의 수학적 공식은 위와 같다.
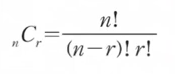
- 조합의 수학적 공식은 위와 같다.
- 순열과 매우 비슷하며 분모에 r!만 추가되어 있는 것을 확인할 수 있다.
- r!은 순서가 다른 경우의 수를 제거하는 역할이다.
1. 특정 문제를 가정하기
- 먼저 적당한 조합 문제를 가정해보자.
- 5개의 데이터에서 3개를 선택하는 조합의 경우의 수를 푸는 문제로 가정
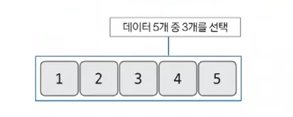
2. 모든 부분 문제가 해결된 상황이라고 가정하고 지금 문제 생각하기
- 5개의 데이터 중 4개를 이미 선택이 완료된 데이터라고 가정하자.
- 그리고 마지막 데이터의 선택 여부에 따른 경우의 수를 계산한다.

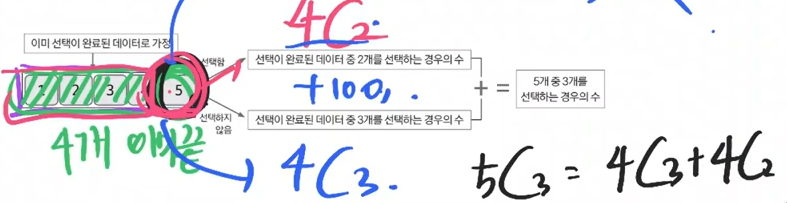
앞 그림을 점화식으로 표현하면 다음과 같다.
- 5개 중 3개를 선택하는 경우의 수 점화식
D[5][3] = D[4][2] + D[4][3]
3. 특정 문제를 해결한 내용을 바탕으로 일반 점화식 도출하기
- 이 일반화된 점화식을 이용하면 조합과 관련된 모든 경우의 수를 쉽게 구할 수 있다.
- 조합 점화식
D[i][j] = D[i - 1][j] + D[i - 1][j - 1]
출처 - 하루코딩

