최소 신장 트리 (MST)

• 최소 신장 트리(minimum spanning tree)란 그래프에서 모든 노드를 연결할 때 사용된 엣지들의 가중치의 합을 최소로하는 트리이다.
  • 크루스칼, 프림 알고리즘 2개로 나뉜다.
  • 여기서는 크루스칼 알고리즘을 다룬다.

🌸 최소 신장 트리의 특징

• 사이클이 포함되면 가중치의 합이 최소가 될 수 없으므로 사이클을 포함하지 않는다.
• N개의 노드가 있으면 최소 신장 트리를 구성하는 엣지의 갯수는 항상 N - 1개다.

최소 신장 트리의 핵심 이론

1. 엣지 리스트로 그래프를 구현하고 유니온 파인드 리스트 초기화하기

• 유니온 파인드는 사이클 판별을 위해서 사용한다.
• 최소 신장 트리는 데이터를 노드가 아닌 엣지 중심으로 저장하므로 인접 리스트가 아닌 엣지 리스트의 형대로 저장한다.
• 이 리스트는 일반적으로 노드 변수 2개와 가중치 변수로 구성된다.
• 사이클 처리를 위한 유니온 파인드 리스트도 함께 초기화한다.
• 리스트의 인덱스를 해당 자리의 값으로 초기화하면 된다.

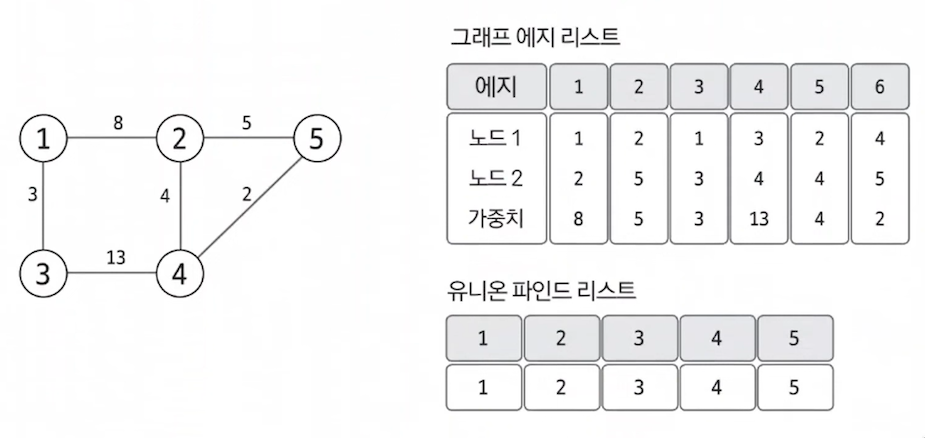
2. 그래프 데이터를 가중치 기준으로 정렬하기

• 엣지 리스트에 담긴 그래프 데이터를 가중치 기준으로 오름차순 정렬한다.

3. 가중치가 낮은 엣지부터 연결 시도하기

• 가중치가 낮은 엣지부터 순서대로 선택에 연결을 시도한다.
• 이 때 바로 연결하지 않고 엣지를 연결했을 때 그래프에 사이클 형성 유무를 find 연산을 이용해 확인한 후 사이클이 형성되지 않을 때만 union 연산을 이용해 두 노드를 연결한다.

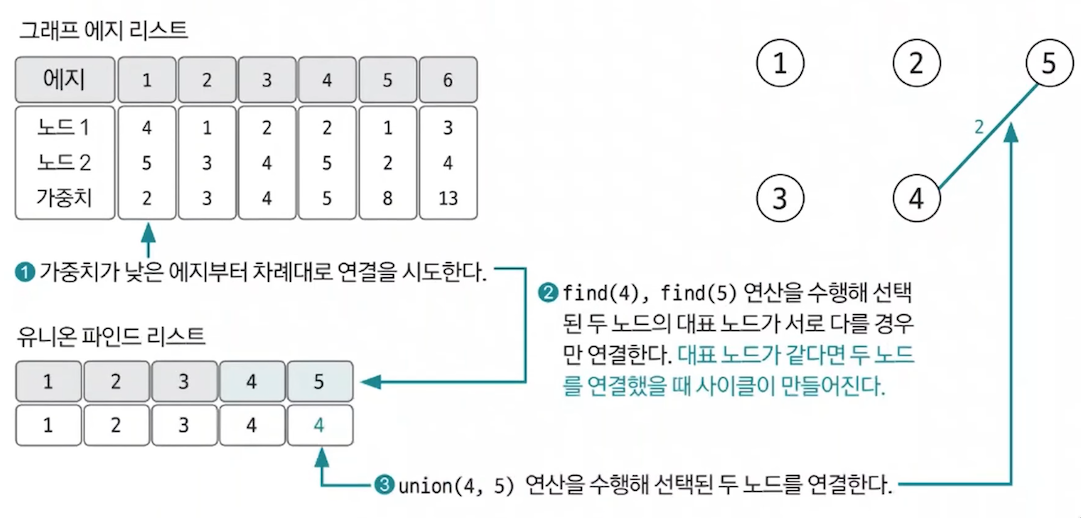
4. 과정 3 반복하기

• 전체 노드의 갯수가 N개이면 연결한 엣지의 갯수가 N - 1이 될 때까지 과정 3을 반복한다.

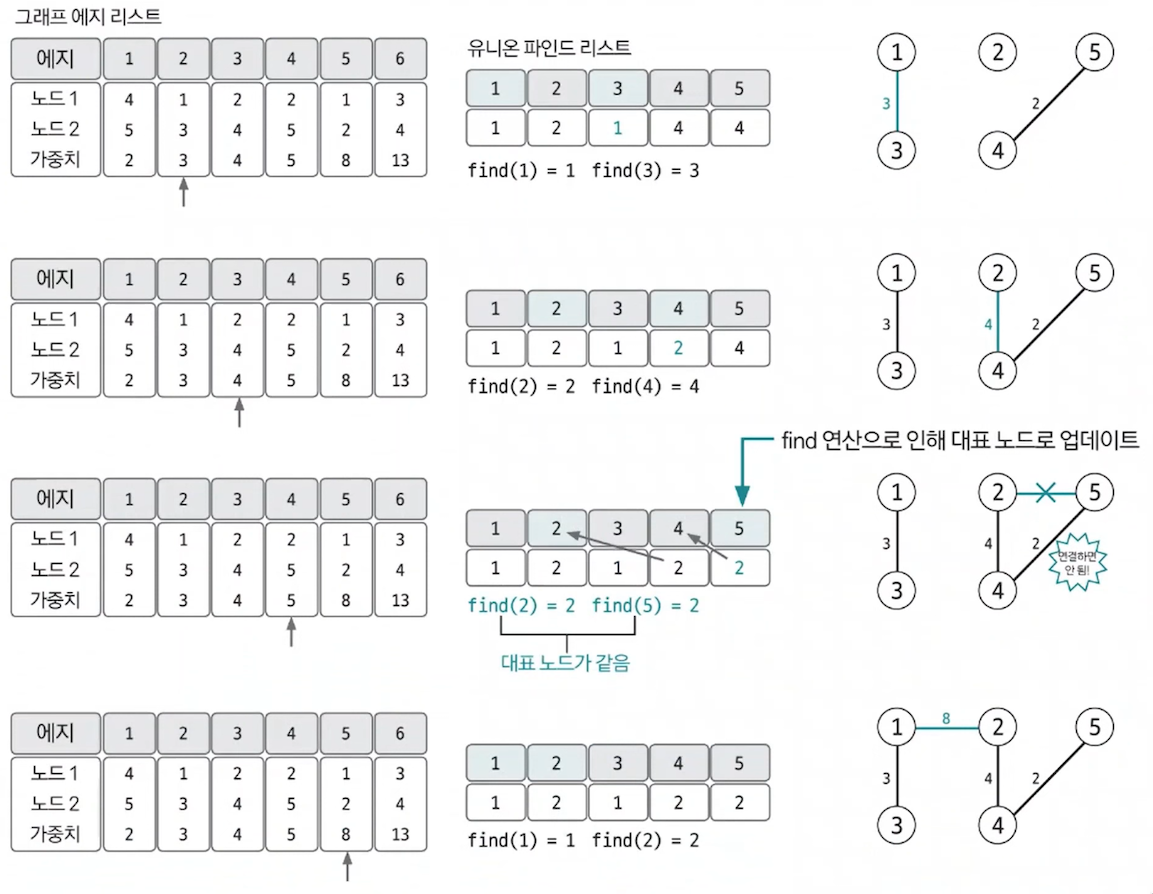
5. 총 엣지 비용 출력하기

• 엣지의 갯수가 N - 1이 되면 알고리즘을 종료하고, 완성된 최소 신장 트리의 총 엣지 비용을 출력한다.

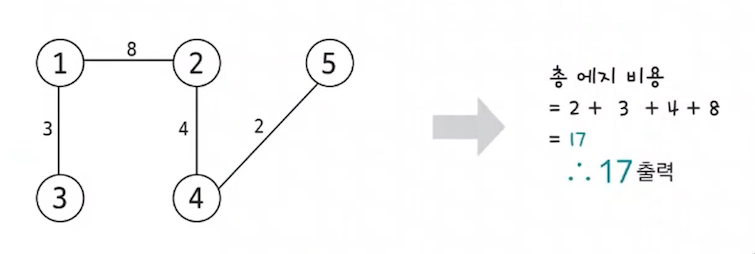
• 최소 신장 트리는 다른 그래프 알고리즘과는 달리, 엣지 리스트의 형태를 이용해 데이터를 담는다는 특징이 있다. 그 이유는 엣지를 기준으로하는 알고리즘이기 때문.
• 또한, 사이클이 존재하면 안되는 특징이 있으므로 사이클 판별 알고리즘인 유니온 파인트 알고리즘을 내부에 구현해야한다.

---

출처 - 하루코딩