💡 세그먼트 트리는 구간 합을 구할때 시간 복잡도가 O(logN)이다.
코드 작성
├── collections
│ ├── segmentTree
│ └── stack
└── pkg
└── mod
└── cache
collections 디렉토리 안에서 go mod init collections 명령어를 통해 모듈을 만들었다.
그 곳에 segementTree 폴더를 만들고 작성을 진행한다.
세그먼트 트리 구성
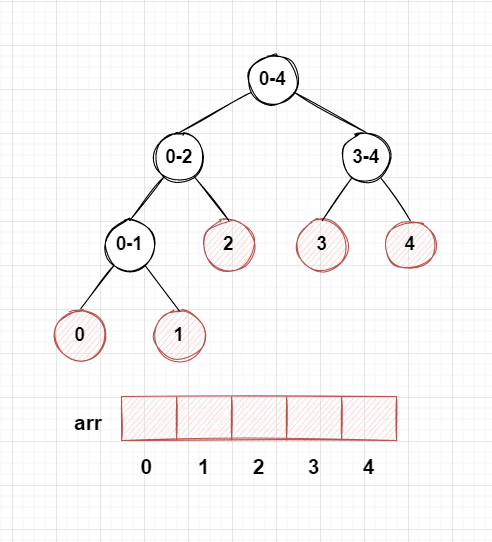
리프 노드는 arr 배열의 값들로 채워 놓고 부모 노드에는 왼쪽 자식과 오른쪽 자식의 합을 저장한다.
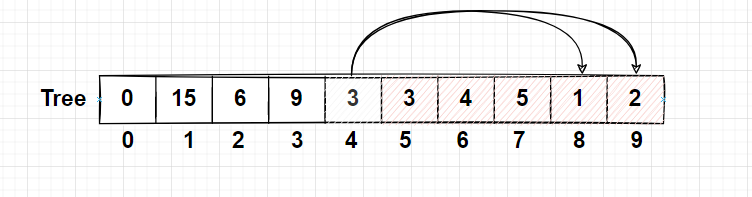
세그먼트 트리는 이진 트리이므로 배열을 선언해 구현할 경우 거의 모든 인덱스에 값을 채울 수 있다.부모 노드의 인덱스가 i라면 왼쪽,오른쪽 자식 노드는 각각 2i, 2i+1이 된다. 자식노드를 계산하기 쉽게하기 위해서 인덱스는 1부터 시작한다.
정확한 tree배열 크기 구하기
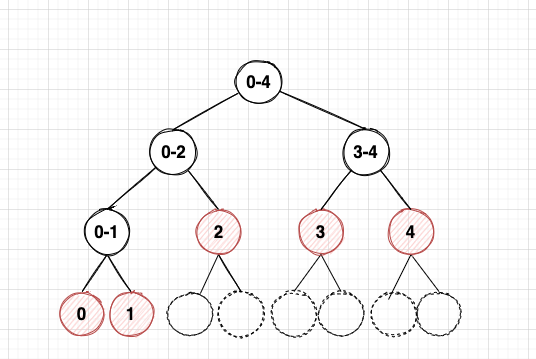
정확한 tree배열의 크기를 정하기 위해서는 세그먼트 트리의 높이를 알아야 한다. 트리의 높이를 H, arr배열 크기를 N이라 했을 때 H = ceil(log2N)이 된다. 거기다 2^(H+1)했을 때 최종적으로 tree배열의 크기가 나온다. 항상 2^(H+1)<4N이기 때문에 공간이 부족하지 않다면 간단하게 tree 크기를 4N으로 한다.
구현해야할 세그먼트 트리의 기능은 3가지 이다.
build: 초기화query: 구간합 구하기update: 변경
모든 기능은 재귀를 이용한다.
type SegmentTree struct {
arr []int
tree []int
}
func New(arr []int) *SegmentTree {
return &SegmentTree{arr, make([]int, 4*len(arr))}
}tree배열의 크기는 트리를 구성하는 노드의 총 갯수를 의미하는데 일단 N*4를 배열 크기로 한다.
build 구현
build 함수를 이용해서 tree배열에 값을 넣는 작업을 수행한다.
// build 세그먼트 트리를 채우는 함수
// start : 배열의 시작 인덱스, end : 배열의 마지막 인덱스
// node : 세그먼트 트리의 인덱스 (1부터 시작)
func (s *SegmentTree) build(start, end, node int) {
// 리프 노드
if start == end {
s.tree[node] = s.arr[start]
return
}
mid := (start + end) / 2
// 좌측 노드와 우측 노드를 채워주면서 부모 노드의 값도 채워준다.
s.build(start, mid, 2*node)
s.build(mid+1, end, 2*node+1)
s.tree[node] = s.tree[2*node] + s.tree[2*node+1]
return
}query 구현
구간합을 구하는 기능을 수행한다. 기본적으로 범위 내에 있다면 값을 반환하고 그렇지 않으면 0을 반환한다.
// query 구간 합을 구하는 함수
// start : 시작 인덱스, end : 마지막 인덱스
// left, right : 구간 합을 구하고자 하는 범위
func (s *SegmentTree) query(start, end, node, left, right int) int {
if (left <= start) && (end <= right) {
return s.tree[node]
}
//범위 밖인 경우
if (right < start) || (end < left) {
return 0
}
mid := (start + end) / 2
leftSum := s.query(start, mid, 2*node, left, right)
rightSum := s.query(mid+1, end, 2*node+1, left, right)
return leftSum + rightSum
}
update 구현
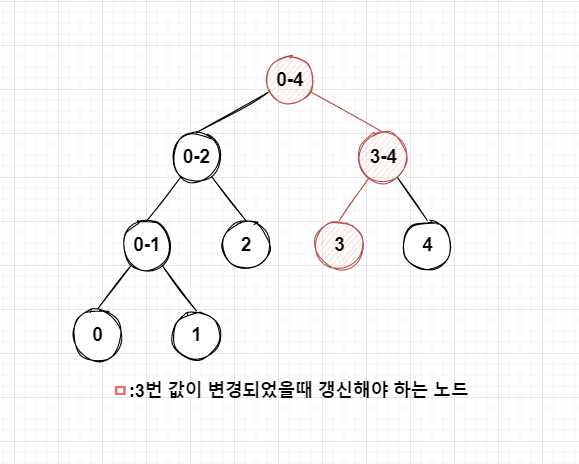
어떤 수를 변경될 경우, 그 숫자의 노드 뿐만 아니라 부모 노드 모두를 변경해야 한다. 앞서 말했듯 재귀를 이용해 구현 할 수 있다.
구간 합일 경우에는 원래값과 수정값의 차이(diff)를 구해 자식 노드와 나머지 노드에 diff를 더하면 되지만 업데이트는 기본적으로 자식노드를 먼저 변경하고, 변경된 정보를 토대로 부모 노드를 변경하는 방향으로 가는 것이 좋다고 한다.
// update 특정 원소의 값을 수정하는 함수
// start : 시작 인덱스
// end : 마지막 인덱스
// node : 세그먼트 트리의 인덱스 (1부터 시작)
// i : 수정하고자 하는 노드의 인덱스
// diff : 원래값-수정 값
func (s *SegmentTree) update(start, end, node, i, diff int) {
//범위에서 벗어남
if (i < start) || (end < i) {
return
}
s.tree[node] += diff
if start != end {
mid := (start + end) / 2
s.update(start, mid, 2*node, i, diff)
s.update(mid+1, end, 2*node+1, i, diff)
}
return
}1105.구간 곱 구하기를 풀어보면 update함수를 위의 방법과 다른 방법으로 구현해야 하는데 위의 방법은 부모노드를 먼저 변경한다.
부모를 먼저 변경해도 되는 경우는 자식의 결과를 몰라도 항상 답을 알 수 있는 경우인데 1105.구간 곱 구하기는 그렇지 않기 때문이다.
적용해보기

기본적인 문제말고 응용문제를 풀어보는 게 세그먼트 트리가 뭔지 더 잘 이해할 수 있는데 응용문제가 정말 많다.
최종코드
package segementTree
type SegmentTree struct {
arr []int
tree []int
}
func New(arr []int, n int) *SegmentTree {
return &SegmentTree{arr, make([]int, n)}
}
// build 세그먼트 트리를 채우는 함수
// start : 배열의 시작 인덱스, end : 배열의 마지막 인덱스
// node : 세그먼트 트리의 인덱스 (1부터 시작)
func (s *SegmentTree) build(start, end, node int) {
// 리프 노드
if start == end {
s.tree[node] = s.arr[start]
return
}
mid := (start + end) / 2
// 좌측 노드와 우측 노드를 채워주면서 부모 노드의 값도 채워준다.
s.build(start, mid, 2*node)
s.build(mid+1, end, 2*node+1)
s.tree[node] = s.tree[2*node] + s.tree[2*node+1]
return
}
// query 구간 합을 구하는 함수
// start : 시작 인덱스, end : 마지막 인덱스
// left, right : 구간 합을 구하고자 하는 범위
func (s *SegmentTree) query(start, end, node, left, right int) int {
if (left <= start) && (end <= right) {
return s.tree[node]
}
if (right < start) || (end < left) {
return 0
}
mid := (start + end) / 2
leftSum := s.query(start, mid, 2*node, left, right)
rightSum := s.query(mid+1, end, 2*node+1, left, right)
return leftSum + rightSum
}
// update 특정 원소의 값을 수정하는 함수
// start : 시작 인덱스
// end : 마지막 인덱스
// node : 세그먼트 트리의 인덱스 (1부터 시작)
// i : 구간 합을 수정하고자 하는 노드
// diff : 원래값-수정 값
func (s *SegmentTree) update(start, end, node, i, diff int) {
//범위에서 벗어남
if (i < start) || (end < i) {
return
}
s.tree[node] += diff
if start != end {
mid := (start + end) / 2
s.update(start, mid, 2*node, i, diff)
s.update(mid+1, end, 2*node+1, i, diff)
}
return
}

