[알고리즘][Kotlin] Topological Sorting

위상 정렬이란 DAG 비순환 방향 그래프에서 노드를 선형으로 정렬하는 알고리즘을 말한다.

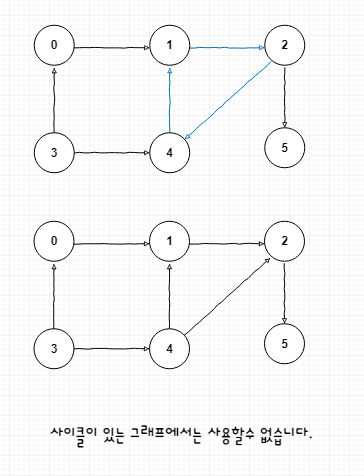
위상정렬은 BFS와 DFS를 응용해서 구현할 수 있는 알고리즘이다. 시간복잡도는 O(V+E)이고 주의할 점은 그래프가 순환한다면 위상 정렬을 사용할 수 없다.

BFS와 DFS 두가지 다 구현해볼 예정이다.

BFS로 구현

BFS로 구현할 경우 진입차수 (Indegree)라는 개념을 이해할 필요가 있다. 진입차수는 노드로 들어오는 간선의 개수를 말한다.

보통 BFS를 구현할 때 방문 체크를 위해 boolean 타입의 visited 배열을 생성한다.
그리고 만약 아직 방문하지 않은 노드라면 queue에 넣는다.
이때 indegree 배열은 visited 배열과 비슷한 역할을 한다.

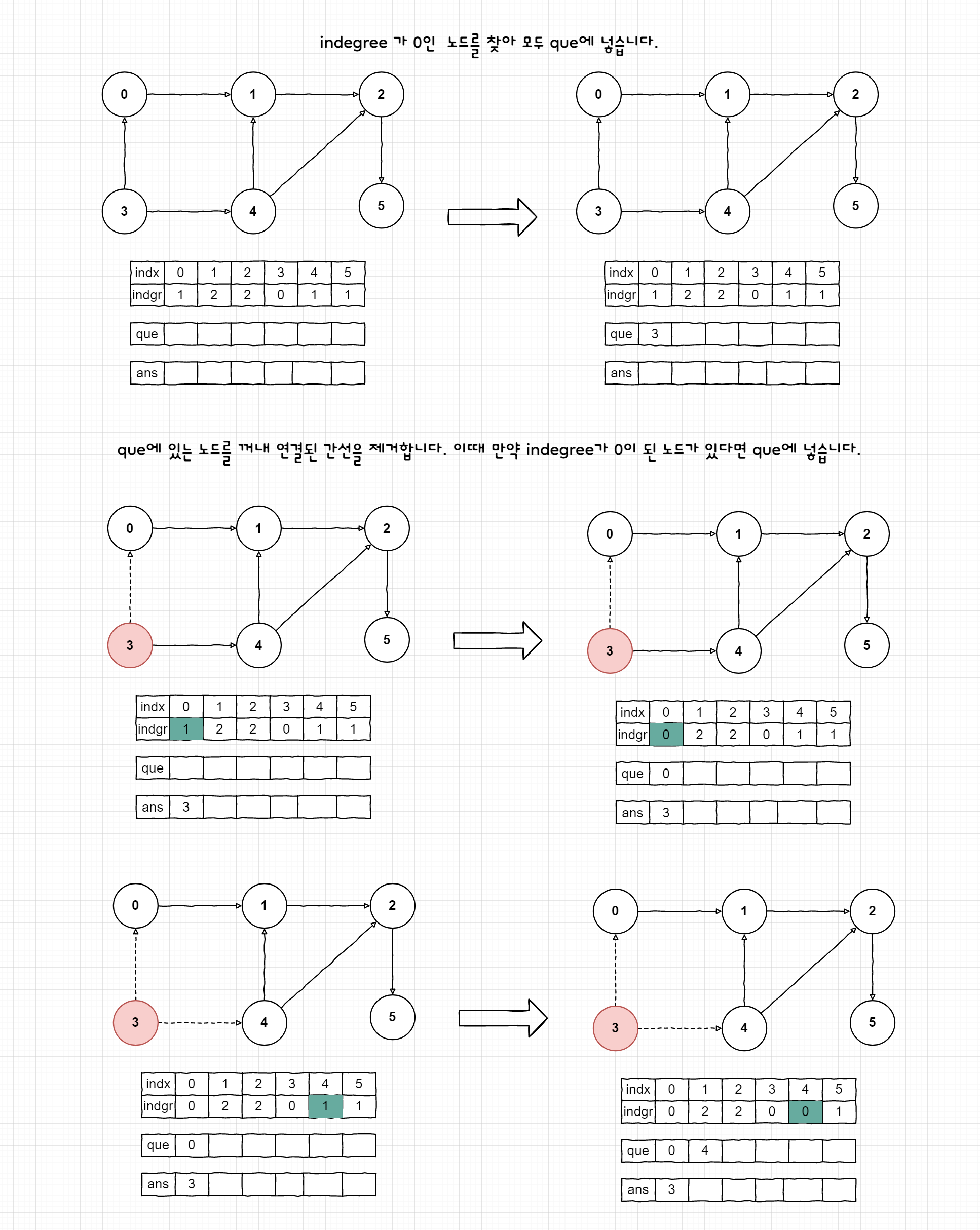
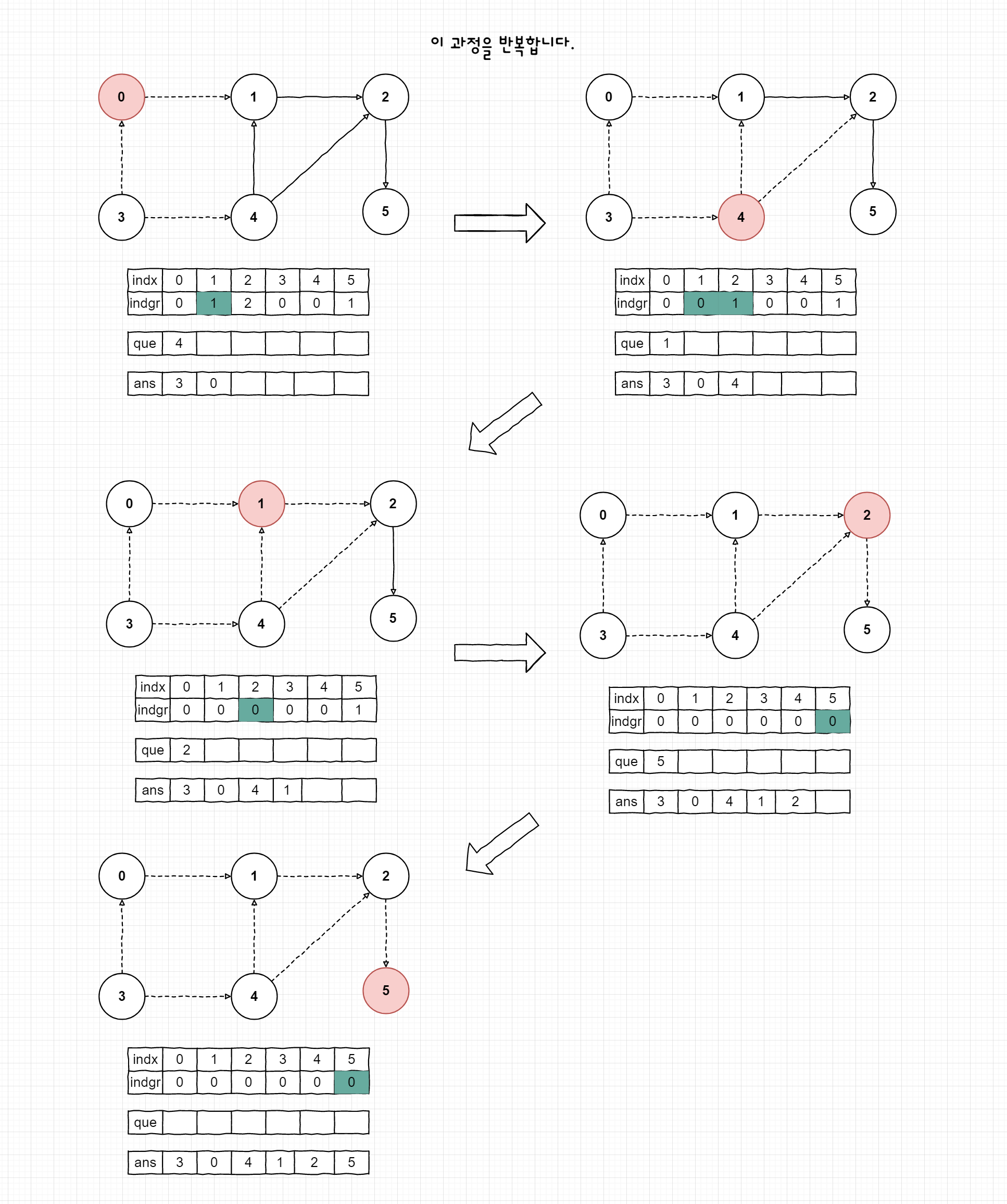
구현 과정은 아래와 같다.

1. 들어오는 간선(indegree)이 없는 정점을 찾아서 큐(Queue)에 넣는다.
2. 큐의 정점의 나가는 간선들을 삭제한다.
3. 큐가 빌 때까지 1-2번을 반복

BFS 코드

import java.util.*
import kotlin.collections.ArrayList

private lateinit var arr:ArrayList<ArrayList<Int>>
private lateinit var indegree:IntArray
private lateinit var answer:ArrayList<Int>

fun main() {
    val (n,m) = readLine()!!.split(" ").map{it.toInt()}
    arr = ArrayList()
    indegree = IntArray(n+1)
    answer = ArrayList()

    //인접리스트 생성
    repeat(n+1){arr.add(ArrayList())}
    //간선 추가
    repeat(m){
        val (start,end) = readLine()!!.split(" ").map{it.toInt()}
        arr[start].add(end)
        // 해당 노드의 진입차수를 추가해 줍니다.
        indegree[end]++
    }
    //bfs
    bfs()
    //순서대로 꺼내 줍니다.
    answer.forEach{ print("${it} ")}
}
private fun bfs(){
    val que = LinkedList<Int>()
	// indegree가 0인 노드를 모두 que에 추가
    indegree.forEachIndexed{index,i->
        if(index!=0&&i==0){
            que.add(index)
        }
    }
    
    while(que.isNotEmpty()){
        val n = que.poll()
        
        answer.add(n)
        
        for(i in arr[n]){
        	// 진입차수를 제거했을때 0이면 que에 추가
            if(--indegree[i]==0){
                que.add(i)
            }
        }
    }
}

DFS로 구현

BFS와 달리 DFS로 구현할 경우 진입차수 (Indegree)를 이용하지 않고 방문 체크를 사용 한다.

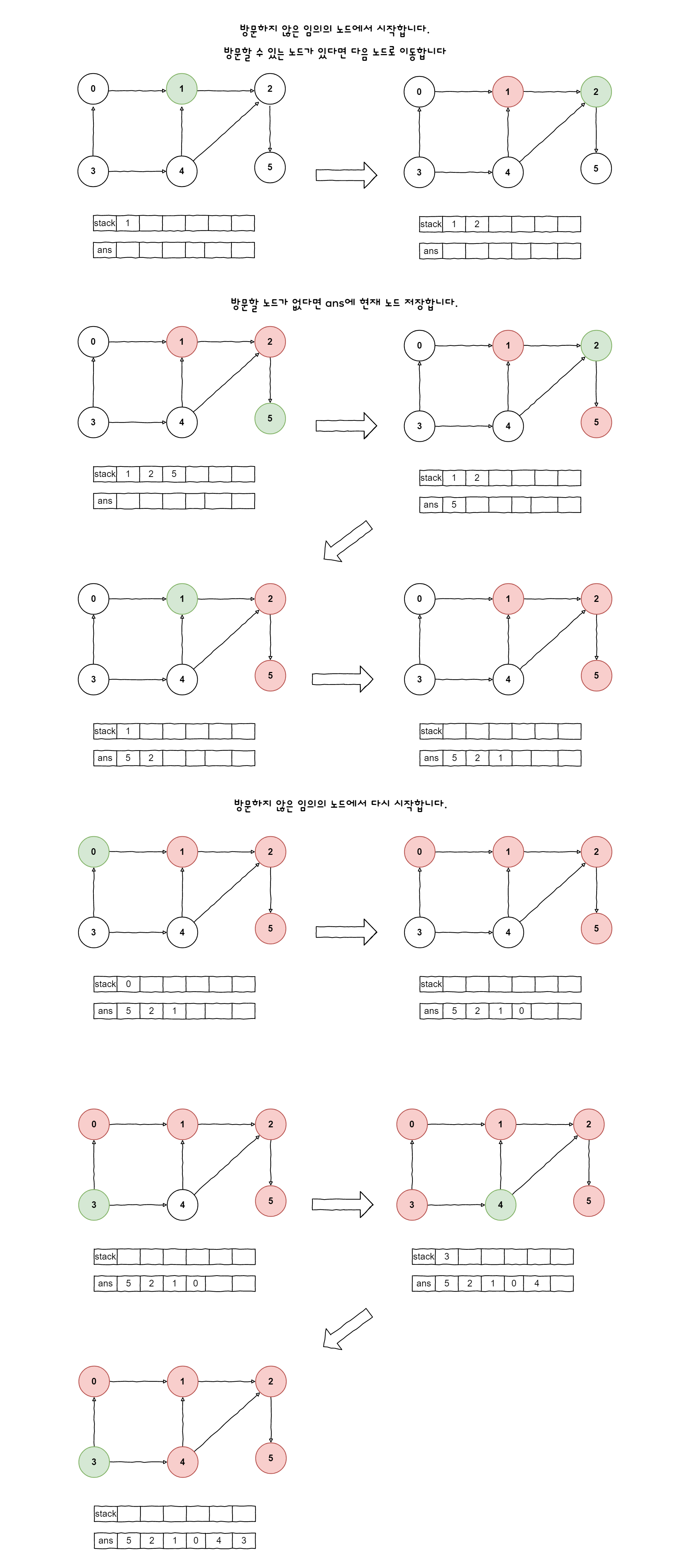
구현 과정은 다음과 같다.

1. 방문하지 않은 임의의 노드에 대해 DFS를 실행
2. 방문할 곳이 없다면 저장
3. 탐색할 곳이 있다면 이동
4. 1-3반복

DFS 코드

import kotlin.collections.ArrayList

private lateinit var arr: ArrayList<ArrayList<Int>>
private lateinit var visited: BooleanArray
private lateinit var answer: ArrayList<Int>

fun main() {
    val (n, m) = readLine()!!.split(" ").map { it.toInt() }
    visited = BooleanArray(n + 1)
    answer = ArrayList()

    //인접리스트
    arr = ArrayList<ArrayList<Int>>().apply {
        //노드 수 만큼 ArrayList생성
        repeat(n + 1) { this.add(ArrayList()) }
        //간선 추가
        repeat(m) {
            val (start, end) = readLine()!!.split(" ").map { it.toInt() }
            this[start].add(end)
        }
    }
    //방문하지 않은 노드에 대해 DFS
//    for (i in 1 .. n){   어떤 노드로 시작 해도 상관없다.
    for (i in n downTo 1) {
        if (visited[i]) continue
        dfs(i)
    }
    // 마지막 부터 꺼내줍니다.
    answer.reversed().forEach { print("$it ") }
}

private fun dfs(num: Int) {
    visited[num] = true
    for (i in arr[num]) {
        if (visited[i]) continue
        // 이동할 노드가 있다면 이동
        dfs(i)
    }
    //더이상 방문할곳이 없다면
    answer.add(num)
}

결과

2252.줄 세우기

BFS가 DFS보다 살짝 더 빠른걸로 나오는데 다른 문제들도 실험해보면 좋을 것 같다.