[코딩테스트] 아방가르드 타일링

문제 바로가기

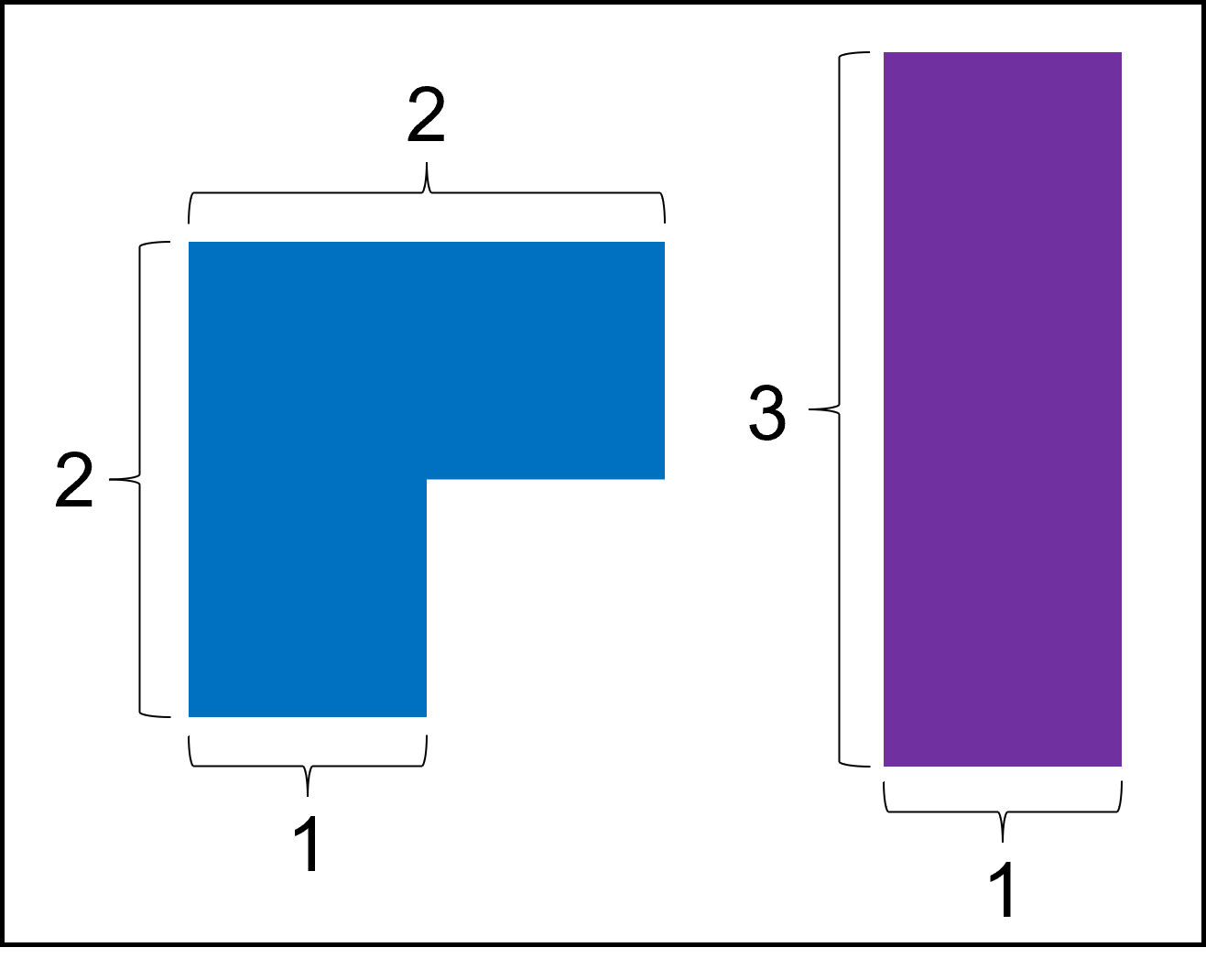위 그림에 제시된 것과 같은 모양의 두 종류의 타일이 있다.
각 타일은 90도마다 회전이 가능한데, 이때 가로 n (n은 자연수), 세로 3으로 타일링을 할 수 있는 경우의 수를 구하는 문제다.

풀이

힌트, 참고 풀이

핵심 풀이법은 점화식을 구하는 일이다.
그런데 이 문제는 점화식을 구하는 것부터 쉽지 않다.
그나마 다행인 점은, n > 3인 경우, 3으로 나눈 나머지가 1, 2, 0일 때 새롭게 추가되는 유형의 타일링이 2, 2, 4개로 반복된다는 점이다. (힌트 참고)
그렇지만 점화식을 확인하기 위해, n = 6까지의 타일링을 할 수 있는 경우의 수는 직접 구해야 했다.

경우의 수를 $S(n)$ 이라 할 때 $S(4) = 23, S(5) = 62, S(6) =170$ 이 나오게 됨을 확인하였는데, 여기서 점화식을 추출해야 한다. n = 4, 5, 6일 때 각각 다음과 같이 추출된다.
$23 = 10 + (2) * 3 + (5) * 1 + (2)$
$62 = 23 + (2) * 10 + (5) * 3 + (2) * 1 + (2)$
$170 = 62 + (2) * 23 + (5) * 10 + (2) * 3 (2) * 1 + (4)$

이를 일반화하면 $S(n) = S(n-1) + 2S(n-2) + 5S(n-3) + 2S(n-4) + 2S(n-5) + 4S(n-6) + ...$ 이 되는데, S(n-4) 항부터는 계수가 2, 2, 4로 반복되는 점을 이용하여 $S(n+3) - S(n)$을 계산 가능하며,
$S(n+3)= S(n+2) + 2S(n+1) + 6S(n) + S(n-1) - S(n-3)$ 이 된다.

이를 정리하여 행렬로 나타내면 다음과 같다.

$\begin{bmatrix}S(n+3)\\S(n+2)\\S(n+1)\\S(n)\\S(n-1)\\S(n-2) \end{bmatrix}$ = $\begin{bmatrix}1&2&6&1&0&-1\\1&0&0&0&0&0\\0&1&0&0&0&0\\0&0&1&0&0&0\\0&0&0&1&0&0\\0&0&0&0&1&0 \end{bmatrix}$ $\begin{bmatrix}S(n+2)\\S(n+1)\\S(n)\\S(n-1)\\S(n-2)\\S(n-3) \end{bmatrix}$

풀이 코드

1. numpy 이용 (런타임 에러)

import numpy as np

def matrix_product(arr, L):
    l = len(arr)
    result = [0] * l
    for i in range(l):
        for j in range(l):
            result[i] += arr[i][j] * L[-j-1]
            result[i] %= 1000000007
    return result%1000000007

def solution(n):
    S = [1, 3, 10, 23, 62, 170]
    if n < 7:
        return S[n-1]
    
    arr = [[1, 2, 6, 1, 0, -1]]
    for i in range(5):
        L = [0] * 6
        L[i] = 1
        arr.append(L)
        
    mtx = [row[:] for row in arr]
    r_matrix = [[0] * 6 for _ in range(6)]
    for i in range(6):
        r_matrix[i][i] = 1
        
    count = n - 3
    while count > 0:
        if count % 2:
            r_matrix = np.dot(r_matrix, mtx)
        mtx = np.dot(mtx, mtx)
        count //= 2
    return matrix_product(r_matrix, S)[3]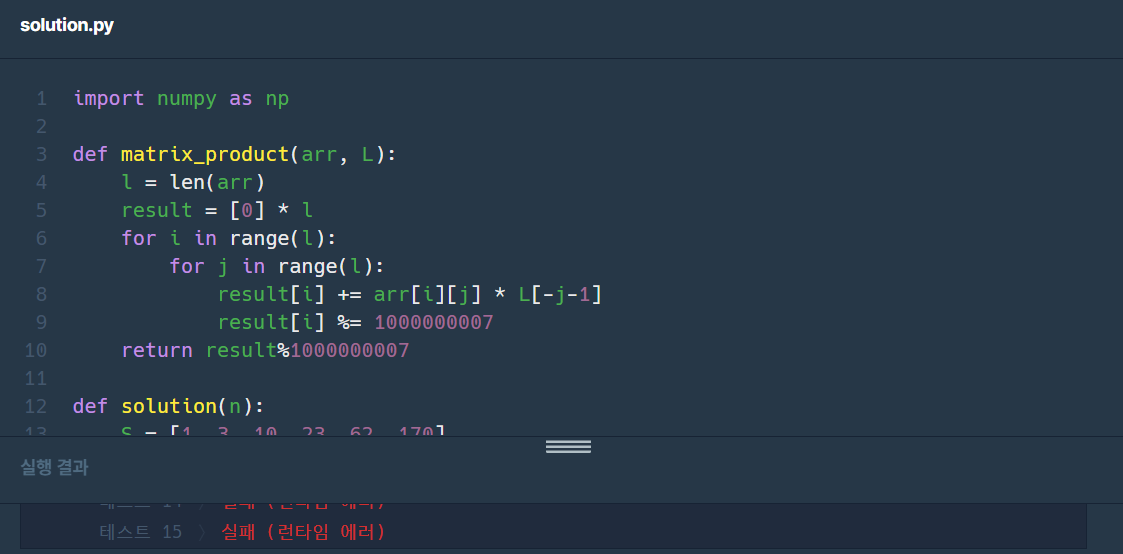

numpy를 쓸 경우 dot이든 matmul을 쓰든 런타임 에러가 발생한다.
그런데 numpy를 쓰지 않고 dot product 함수를 직접 정의할 때도 에러가 발생하는데, 그 이유로는 직접 만든 함수 안에서 1,000,000,007로 나누는 값을 return해서 런타임 에러가 난다고 생각했다.

따라서 1,000,000,007을 mod라는 변수에 부여하였으며, numpy를 import하지 않고 내적함수를 직접 정의하여 아래와 같은 코드를 구현하였다.

mod = 1000000007

def dot_product(arr1, arr2):
    l = len(arr1)
    new_arr = [[0] * l for _ in range(l)]
    for i in range(l):
        for j in range(l):
            for k in range(l):
                new_arr[i][j] += arr1[i][k] * arr2[k][j]
            new_arr[i][j] %= mod
    return new_arr

def matrix_product(arr, L):
    l = len(arr)
    result = [0] * l
    for i in range(l):
        for j in range(l):
            result[i] += arr[i][j] * L[-j-1]
            result[i] %= mod
    return result

def solution(n):
    S = [1, 3, 10, 23, 62, 170]
    if n < 7:
        return S[n-1]
    
    arr = [[1, 2, 6, 1, 0, -1]]
    for i in range(5):
        L = [0] * 6
        L[i] = 1
        arr.append(L)
        
    mtx = [row[:] for row in arr]
    r_matrix = [[0] * 6 for _ in range(6)]
    for i in range(6):
        r_matrix[i][i] = 1
        
    count = n - 3
    while count > 0:
        if count % 2:
            r_matrix = dot_product(r_matrix, mtx)
        mtx = dot_product(mtx, mtx)
        count //= 2
    return matrix_product(r_matrix, S)[3]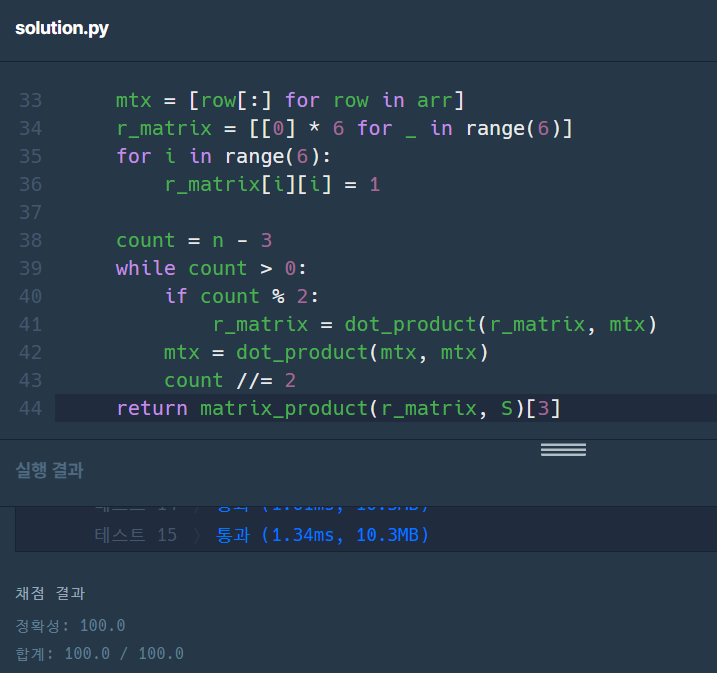

후기

다른 참고 코드를 볼 수 있었던 것이 운이 좋았다.
답을 참조하고 풀긴 했지만 답을 이해하는 과정도 쉽지 않았던 것 같다.
점화식을 구하면 되는 문제니 쉽게 풀 수 있을 것이라 생각했지만 알고 보니 노가다성이 좀 있는 문제였다는 건 반전.