전기화학임피던스 분광법(EIS) 2

지난 포스팅에선 추출된 nyquist plot에서 눈대중으로 원에 맞는 부분에 대해서 원 피팅을 하여 배터리 내부저항과 분극저항을 구했다.

이번 포스트에서는 와버그 저항성분(nyquist plot에서 오른쪽 위로 올라가는 성질)까지 고려하여 피팅을 해 보았다.
그놈의 지겨운 피팅놀이는 여기까지 할 것 같다 ㅋㅋ

목표오차함수는 각 주파수지점의 거리제곱 합으로 정의했고,
주파수는 1000hz 부터 0.1hz까지의 임피던스 데이터를 사용했다.
배터리 모델은

위 사진에서 왼쪽 모델을 사용했다.
사실 오른쪽 모델이 가장 일반적으로 사용되는 모델 중 하나지만 와버그 저항이 병렬 항으로 ㄷㄹ어갈경우 식이 굉장히 복잡해져서 코드에 집어넣기 매우 힘들어진다..

그렇게 x저항(R_re), y저항(R_im)을 구해서 w에 따른 좌표를 2차원 scatter를 해 보면

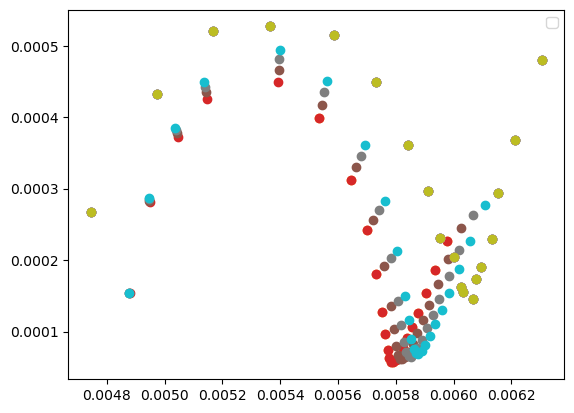
이와 같은데 초록 점이 측정된 나이키스트선도이고 나머지 점들은 점차 학습되어가는 선도이다. 모멘텀 경사하강으로 300회 학습마다 scatter를 찍은 것이며
bds에서 찍혀나오는 Rs,Rp값 대비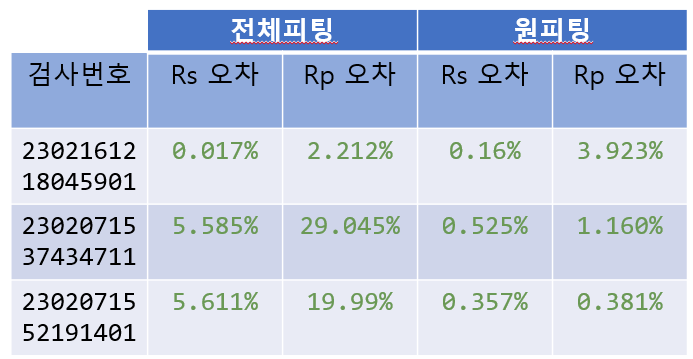
상당히 많은 오차를 수반했다.
이는 아마 모델이 틀렸을 확률이 가장 크고, local minimum에 수렴했을 확률도 있다.
아마 더 좋은 배터리모델을 적용하고, 배터리별로 어느정도 global minimum에 가까운 파라미터를 사전에 알고 있어야 최적화가 잘 될 것 같다.

코드는 다음과 같다. 미분 자체는 해석적으로 하느라 코드가 길어졌다.

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from matplotlib.pylab import rcParams
from tqdm import tqdm
def create_nyquist(R1, R2, C, A, t):
    t=np.array([1000,500,333,250,143,100,66.7,47.6,33.3,21.7,15.2,10,6.8,4.7,3.3,2.2,1.5,1,0.68,0.47,0.33,0.22,0.15,0.1])
    w=2*np.pi*t
    a,b=[],[]
    for i in w:
        #plt.scatter(x(R1,R2,C,A,i), y(R1,R2,C,A,i))
        a+=[x(R1,R2,C,A,i)]
        b+=[y(R1,R2,C,A,i)]
    dfit=pd.DataFrame({'hz':t.tolist(),'re':a,'im':b})
    return dfit

def x(R1, R2, C, A, w):
    return R2 / ((w * C * R2) ** 2 + 1) + A / (w ** (1 / 2)) + R1
def y(R1, R2, C, A, w):
    return w * C * R2**2 / ((w * C * R2) ** 2 + 1) + A / (w ** (1 / 2))
def x_R1(R1, R2, C, A, w):
    return R2 / ((w * C * R2) ** 2 + 1) + A / (w ** (1 / 2))
def x_R2(R1, R2, C, A, w):
    return 1/((w * C * R2) ** 2 + 1)-R2*2*(w*C*R2)*w*C/((w*C*R2)**2+1)**2+A / (w ** (1 / 2)) + R1
def x_C(R1, R2, C, A, w):
    return -R2*2*(w*C*R2)*w*R2/((w*C*R2)**2+1)**2
def x_A(R1, R2, C, A, w):
    return 1/w**(1/2)
def y_R1(R1, R2, C, A, w):
    return 0
def y_R2(R1, R2, C, A, w):
    return 2*w*C*R2/(((w * C * R2) ** 2 + 1)) - w*C*R2**2*2*(w*C*R2)*w*C/(((w * C * R2) ** 2 + 1))**2
def y_C(R1, R2, C, A, w):
    return w*R2**2/((w * C * R2) ** 2 + 1)-w*C*R2**2*2*(w*C*R2)*w*R2/(((w * C * R2) ** 2 + 1))**2
def y_A(R1, R2, C, A, w):
    return 1/w**(1/2)
def E_R1(R1, R2, C, A):
    sum=0
    for j in range(len(t[cut:])):
        i=t[j+cut]
        sum+=2*x_R1(R1, R2, C, A, 2*np.pi*i)*(dfit.re.iloc[j]-df.re.iloc[j])
        #sum+=2*y_R1(R1, R2, C, A, 2*np.pi*i)*(dfit.im.iloc[j]-df.im.iloc[j])
    return sum
def E_R2(R1, R2, C, A):
    sum=0
    for j in range(len(t[cut:])):
        i=t[j+cut]
        sum+=2*x_R2(R1, R2, C, A, 2*np.pi*i)*(dfit.re.iloc[j]-df.re.iloc[j])
        #sum+=2*y_R2(R1, R2, C, A, 2*np.pi*i)*(dfit.im.iloc[j]-df.im.iloc[j])
    return sum
def E_C(R1, R2, C, A):
    sum=0
    for j in range(len(t[cut:])):
        i=t[j+cut]
        sum+=2*x_C(R1, R2, C, A, 2*np.pi*i)*(dfit.re.iloc[j]-df.re.iloc[j])
        #sum+=2*y_C(R1, R2, C, A, 2*np.pi*i)*(dfit.im.iloc[j]-df.im.iloc[j])
    return sum
def E_A(R1, R2, C, A):
    sum=0
    for j in range(len(t[cut:])):
        i=t[j+cut]
        sum+=2*x_A(R1, R2, C, A, 2*np.pi*i)*(dfit.re.iloc[j]-df.re.iloc[j])
        #sum+=2*y_A(R1, R2, C, A, 2*np.pi*i)*(dfit.im.iloc[j]-df.im.iloc[j])
    return sum
def learning(R1, R2, C, A,v):
    learning_rate=0.00001
    r=0.1  
    v[0]=r*v[0]-learning_rate*E_R1(R1, R2, C, A)
    v[1]=r*v[1]-learning_rate*E_R2(R1, R2, C, A)
    v[2]=r*v[2]-learning_rate*E_C(R1, R2, C, A)
    v[3]=r*v[3]-learning_rate*E_A(R1, R2, C, A)
    R1  +=v[0]
    R2  +=v[1]
    C   +=v[2]
    A   +=v[3]
    return R1,R2,C,A,v
# %%
cut=5
df = pd.read_csv("C:/Users/pmgrow/OneDrive - 피엠/바탕 화면/eis.csv")
df = df[df.insp_sq == 2302071552191401][["hz", "re", "im"]][:24].reset_index(drop=True)
df.im = -df.im
#%%
df=df[cut:]
t=np.array([1000,500,333,250,143,100,66.7,47.6,33.3,21.7,15.2,10,6.8,4.7,3.3,2.2,1.5,1,0.68,0.47,0.33,0.22,0.15,0.1])
R1, R2=0.004850308070276534 ,0.0009019052497186386
C, A=1.022837624904952 ,1.795498770154788e-04
dfit=create_nyquist(R1,R2,C,A,t)
dfit=dfit[cut:]
#%%
plt.scatter(df.re, df.im)
plt.scatter(dfit.re,dfit.im)
v=[0,0,0,0]
error=((df-dfit)**2).sum().sum()
r=0.9
for i in tqdm(range(1000)):
    R1,R2,C,A,v=learning(R1, R2, C, A,v)
    dfit=create_nyquist(R1,R2,C,A,t)
    if i%300==0:
        plt.scatter(df.re, df.im)
        plt.scatter(dfit.re,dfit.im)
plt.legend()
print(((df-dfit)**2).sum().sum()/error)        
print(R1,R2,C,A)
# %%
"""
insp_sq:2302161218045901 
R1, R2=0.004750214903933416, 0.0015372215122571478
C, A=0.7022837504179849, 5.9524174418708495e-05
오차: rs: 0.017% rp: -2.212%

insp_sq:2302071537434711
R1,R2=0.004850553712629513, 0.001119669711767384
C,A=1.0228376233080303, 0.0002867494011425674
오차: rs:5.585% rp:29.045%

insp_sq:2302071552191401
R1,R2=0.004850707421761088, 0.001236200820737827
C,A=1.0228376142534317, 0.00031311379658291287
오차: rs:5.611% rp:19.99%

"""

이렇게 EIS 커브피팅을 해 보았는데 보통 연구에서는 피팅프로그램을 쓰는 것 같다.
z-view라는 유료 프로그램이 대표적이고,
나는 EIS spectrum Analyser 라는 프로그램을 써 보았다. 이에대해 간단하게 소개만 하고 포스팅을 마치겠다

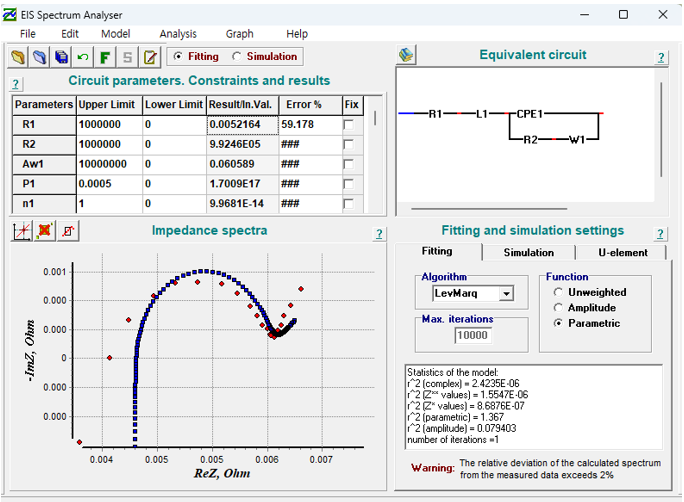
위 사진에서 우상단에 모델과 좌상단의 파라미터 초기값과 범위설정을 할 수 있고, 우 하양에서는 최적화 알고리즘과 최적화함수 등을 선택할 수 있다.

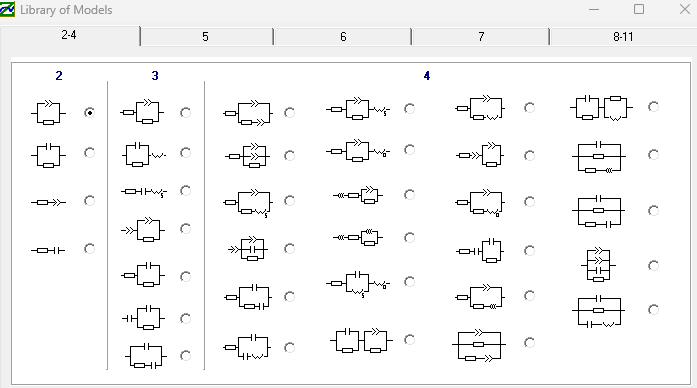
모델의 경우 샘플 모델에서 시작해서 파라미터들을 바꾸고 더해서 원하는 모델로 바꿀 수 있다.

근데 이 프로그램도 초기값선정(local minimum)문제에서 자유롭지 못해서 배터리 파라미터들에 대한 어느정도 범위감각이 있는 배터리 고수들만이 잘 다룰 수 있을 것 같다.