📜 문제 이해하기
자연수 N과 정수 K가 주어졌을 때 이항 계수
(N K)를 1,000,000,007로 나눈 나머지를 구하는 프로그램을 작성하시오.
💡 문제 재정의
자연수 N개중에서 K개를 고르는 조합의 개수를 1000000007 나눈다.
✏️ 계획 수립
이항계수 N개중 K개를 고르는 것의 수는 다음과 같다.
N!/K!(N-K)!
하지만 이 문제의 핵심은 입력의 범위이다. N의 범위가 최대 4백만까지 될 수 있는데 위 팩토리얼을 그대로 사용한다면 당연히 시간초과가 발생하고 DP를 이용해도 O(N²)이기에 시간 초과가 발생한다. 따라서 정수론을 이용하여 문제를 해결하기로 했다.
이때 나누는 수 1000000007가 소수임을 이용하자. 1000000007을 소수 P라고 정의하여 서술한다.
1) Factorial 함수 구현
기존의 math.factorial은 값이 점점 커지고 그에 따라 곱셈에 오랜 시간이 걸린다. 따라서 modular 함수의 성질을 이용해 factorial을 직접 구현하되 모든 곱셈에 대해 modular 연산을 취한다.
2) Modular 곱셈의 성질
A B mod c = (A mod c B mod c) mod c라는 성질이 존재한다. 따라서 N!/K!(N-K)! mod p를 N!(K!(N-K)!)^-1 mod p로 바꾸고 (N! mod p (K!(N-K)!)^-1 mod p) mod p로 변경한다.
3) 곱셈의 역원 구하기
페르마의 소정리를 이용할 수 있다. !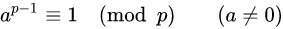
a^p-1은 a^p-2 * a로 정리할 수 있고 a^p-2가 a의 곱셈의 역원이 됨을 확인할 수 있다.
하지만 a^p-2도 터무니없이 큰 수 이다. a는 최대 4백만이고 p-2 1000000005이기 때문이다.
4) 연속 제곱법
연속 제곱법을 사용하면 지수항이 큰 수라도 빠르게 계산할 수 있다.
위 방법을 전부 서술하기에는 너무 많기에 아래 링크를 첨부하였다.
연속제곱법 설명 [울프람알파]
위 방법을 전부 사용하여 구현한다면 빠른 시간내에 이항 계수를 구할 수 있다.
💻 계획 수행
import math
def successive_squaring(a, s, p):
square_list = [a]
# 연속 제곱법
bin_s = bin(s)[2:]
bit_count = len(bin_s) - 1
result = 1
count = 0
while bit_count > count:
square_list.append(square_list[count] ** 2 % p)
count += 1
for i, b in enumerate(bin_s):
if b == '1':
result *= square_list[bit_count - i]
result %= p
return result
def factorial(n, p):
result = 1
while n > 1:
result = result * n % p
n -= 1
return result
if __name__ == '__main__':
n, k = map(int, input().split())
p = 1000000007
numer = factorial(n, p)
denom_inverse = successive_squaring(factorial(k, p) * factorial(n - k, p), p - 2, p)
print(numer * denom_inverse % p)🤔 회고
이전 이항 계수 문제에 비해 정수론을 어느정도 알아야 풀 수 있는 문제였다. 나 또한 오랜만에 정수론을 다루기에 조금 헷갈려서 인터넷을 검색하면서 문제를 해결하였다. 틈틈히 정수론을 공부해야겠다.
