goal
- Graph
- Tree
- Binary Search Tree
1. Graph
- Graph란?
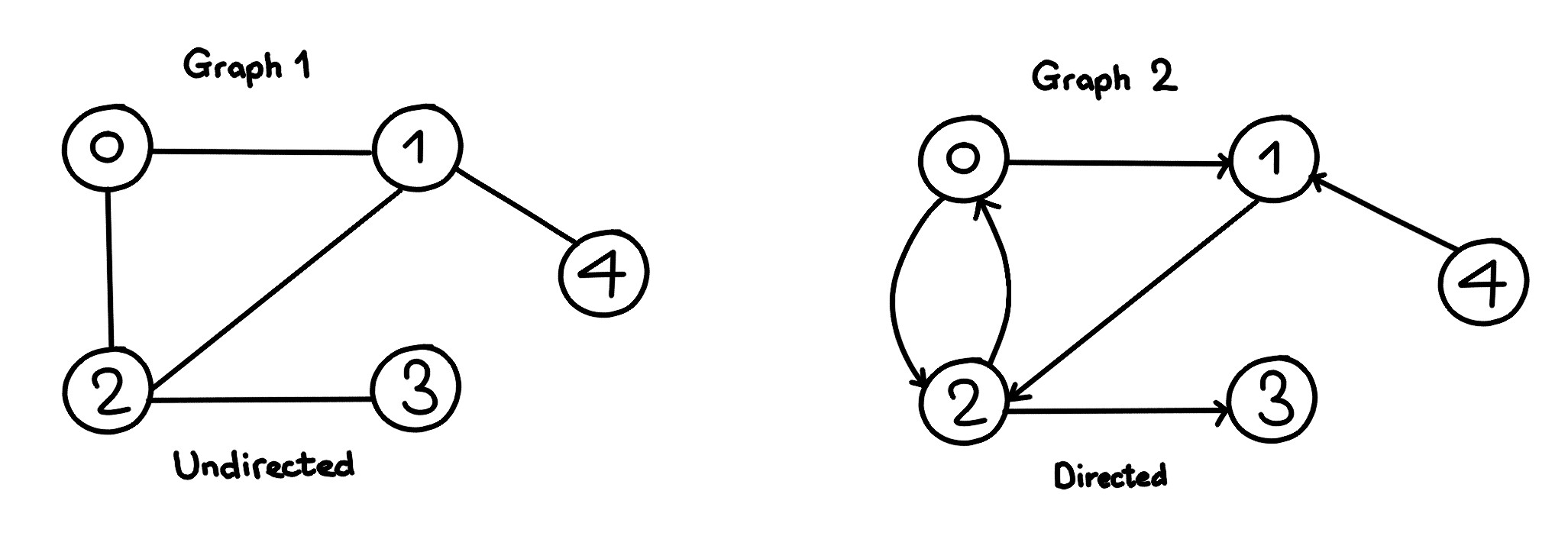
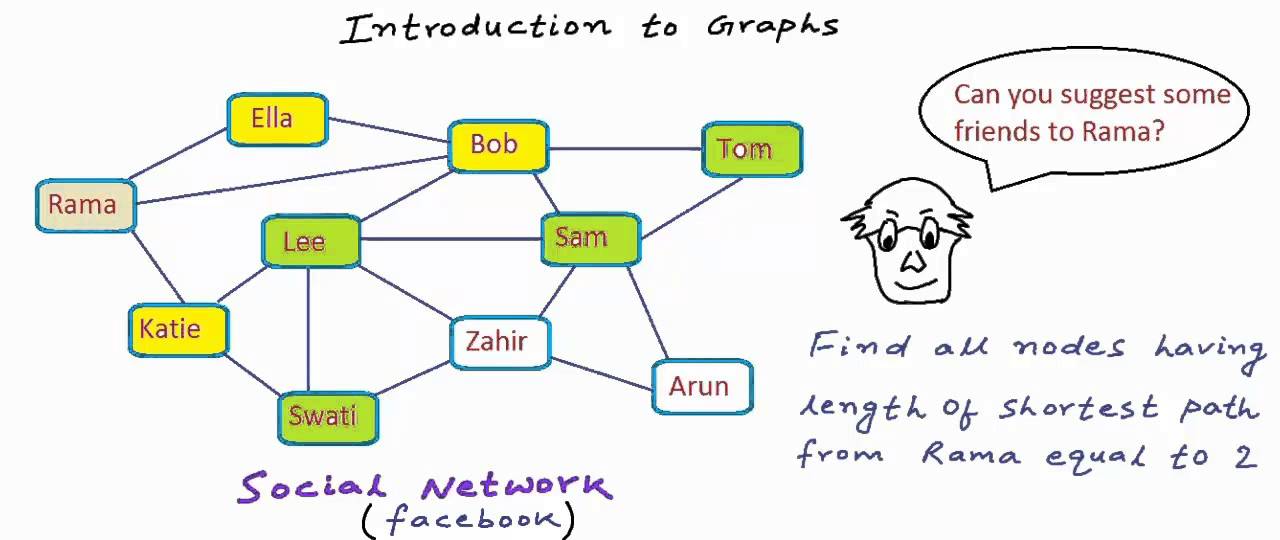
- 트리 구조에서 edge가 방향을 위->아래, 아래->위 로 움직이고, 방향을 안 가질 수도 있고, 들어오는 방향이 여러 곳이 될 수도 있고, 주변의 노드들과 주고 받을 수도 있고, 돌고돌아 써클이 생길수도 있고 하는 자료구조 (트리는 그래프의 한 종류) / 그래프는 vertex와 edge로 구성된 한정된 자료구조를 의미
- 개념
-
노드 (Node or 정점 -vertex- 이라고도 부름), 그리고 노드와 노드를 연결하는 간선(edge)으로 구성
-
그래프 구조와 그래프 관리에 사용되는 알고리즘에 영향을 받음
-
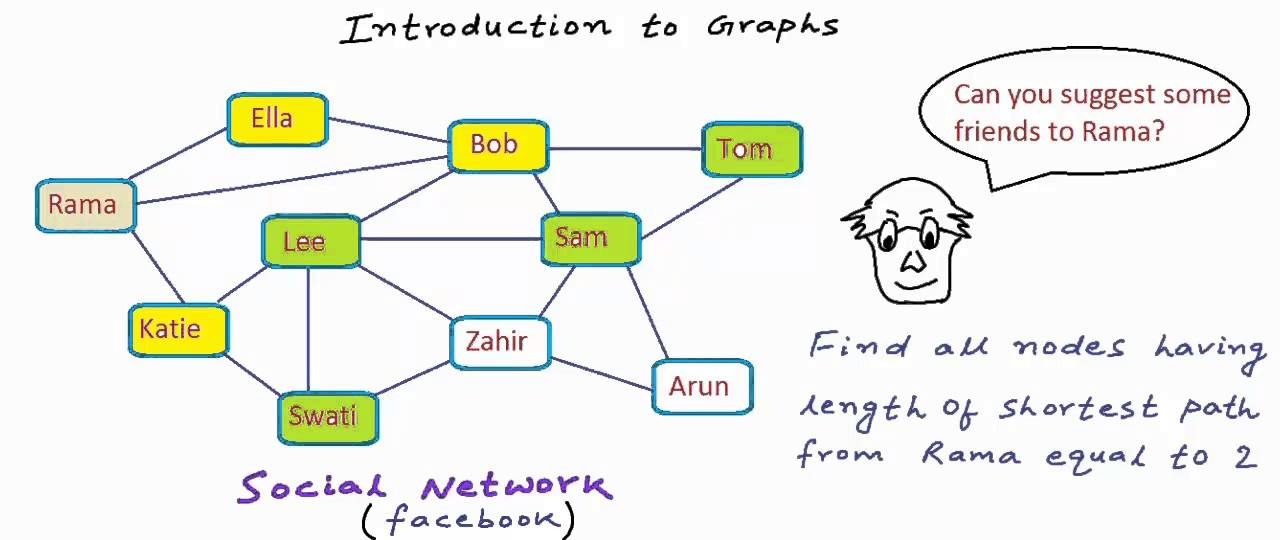
그래프 실생활 예 : 구글 검색
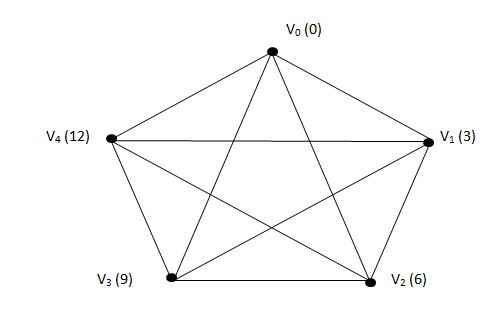
** 여기서 문제 1)
- 종류 (그래프 구현)
1) 인접 행렬 (Adjacent matrix)
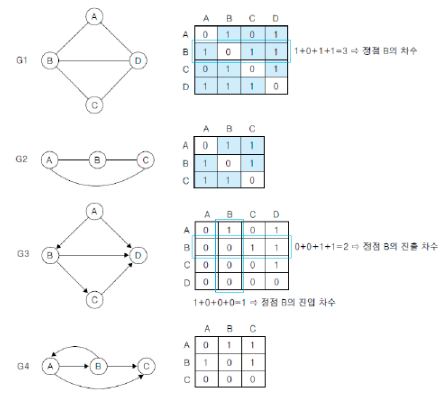
- 개념 : (이어져있으면 1 / 아니면 0 / 으로 정리된) 그래프에서 어느 꼭짓점들이 변으로 연결되었는지 나타내는 정사각 행렬 (=행렬에 대한 2차원 배열을 사용하는 순차 자료구조 방법)
** 수학에서의 행렬은 : 수 또는 다항식 등을 직사각형 모양으로 배열한 것 - 그래프의 두 정점을 연결한 간선의 유무를 행렬로 저장
- n개의 정점을 가진 그래프 : n x n 정방행렬
- 행렬의 행번호와 열번호 : 그래프의 정점
- 행렬 값 : 두 정점이 인접되어 있으면 1, 인접되어 있지 않으면 0
- 무방향 그래프의 인접 행렬
- 행 i 의 합 = 열 i 의 합 = 정점 i 의 차수
- 방향 그래프의 인접 행렬
- 행 i 의 합 : 정점 i 의 진출차수
- 열 i 의 합 : 정점 i 의 진입차수
- 단점
- n개의 정점을 가지는 그래프를 항상 nxn개의 메모리 사용
- 정점의 개수에 비해서 간선의 개수가 적은 희소 그래프에 대한 인접 행렬은 희소 행렬이 되므로 메모리의 낭비 발생
2) 인접 리스트 (Adjacent matrix)
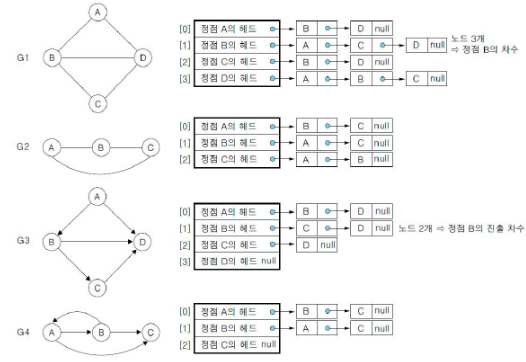
- 개념 : 각 정점에 대한 인접 정점들을 연결하여 만든 단순 연결 리스트
- 각 정점의 차수만큼 노드를 연결
- 리스트 내의 노드들은 인접 정점에 대해서 오름차순으로 연결
- 인접 리스트의 각 노드
- 정점을 저장하는 필드와 다음 인접 정점을 연결하는 링드 필드로 구성
- 정점의 헤드 노드
- 정점에 대한 리스트의 시작을 표현
- n개의 정점과 e개의 간선을 가진 무방향 그래프의 인접 리스트
- 헤드 노드 배열의 크기 : n
- 연결하는 노드의 수 : 2e
- 각 정점의 헤드에 연결된 노드의 수 : 정점의 차수
- n개의 정점과 e개의 간선을 가진 방향 그래프의 인접 리스트
- 헤드 노드 배열의 크기 : n
- 연결하는 노드의 수 : e
- 각 정점의 헤드에 연결된 노드의 수 : 정점의 진출 차수
- 그래프 순회(Graph traversal) / 그래프 탐색(Graph search) 방법
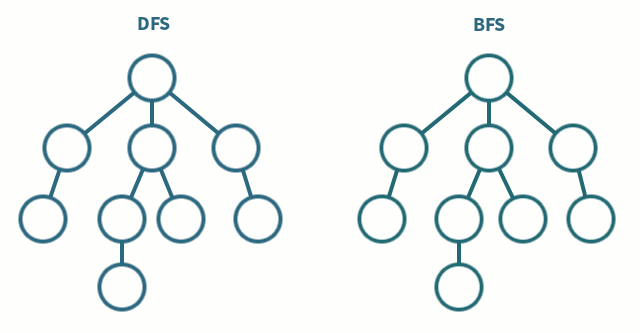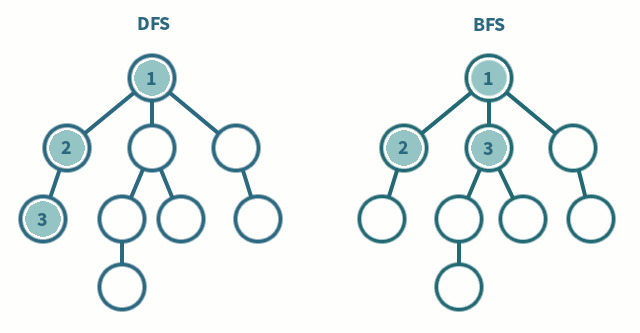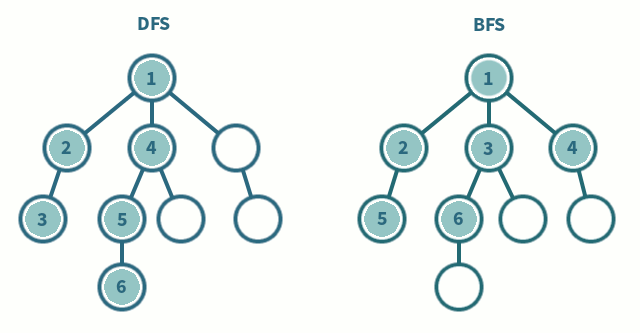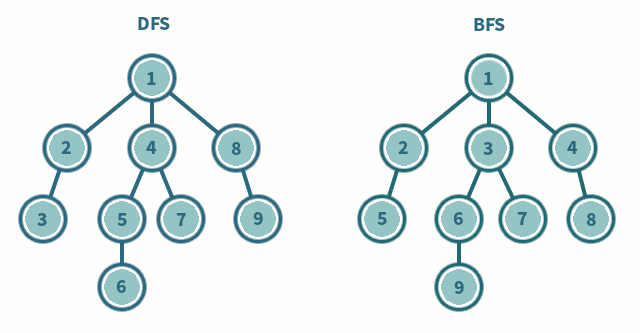
1) 깊이 우선탐색 (DFS, Depth-First Search)
: 루트 노드(혹은 다른 임의의 노드)에서 시작해서 다음 분기(branch)로 넘어가기 전에 해당 분기를 완벽하게 탐색하는 방법
- 자기 자신을 호출하는 순환 알고리즘의 형태를 지님
- 미로를 탐색할 때 한 방향으로 갈 수 있을 때까지 계속 가다가 더 이상 갈 수 없게 되면 다시 가장 가까운 갈림길로 돌아와서 이곳으로부터 다른 방향으로 다시 탐색을 진행하는 방법과 유사함
- 가장 마지막에 만났던 갈림길 간선의 정점으로 가장 먼저 되돌아가서 다시 깊이 우선 탐색을 반복해야 하므로, 후입선출 구조의 스택 사용
- 즉 넓게(wide) 탐색하기 전에 깊게(deep) 탐색함
- 모든 노드를 방문하고자 하는 경우에 이 방법을 선택함
- 깊이 우선 탐색(DFS)이 너비 우선 탐색(BFS)보다 좀 더 간단함
- 검색 속도 자체는 너비 우선 탐색(BFS)에 비해서 느림
- 수행 순서
(1) 시작 정점 a를 결정하여 방문한다.
(2) 정점 a에 인접한 정점 중에서
ㄱ. 방문하지 않는 정점 b가 있으면, 정점 a를 스택에push하고 정점 b를 방문한다. 그리고 b를 a로 하여 다시 (2)를 반복한다.
ㄴ. 방문하지 않은 정점이 없으면, 탐색의 방향을 바꾸기 위해서 스택을pop하여 받은 가장 마지막 방문 정점을 a로 하여 다시 (2)를 반복한다.
(3) 스택이 공백이 될 때까지 (2)를 반복한다.
2) 너비 우선탐색 (BFS, Breadth-First Search)
: 루트 노드(혹은 다른 임의의 노드)에서 시작해서 인접한 노드를 먼저 탐색하는 방법 /
- 시작 정점으로부터 가까운 정점을 먼저 방문하고 멀리 떨어져 있는 정점을 나중에 방문하는 순회 방법
- 가까운 정점들에 대해서 차례로 다시 너비우선 탐색을 반복해야 하므로, 선입선출의 구조를 갖는 큐를 사용
- 즉 깊게(deep) 탐색하기 전에 넓게(wide) 탐색하는 것
- 두 노드 사이의 최단 경로 혹은 임의의 경로를 찾고 싶을 때 이 방법을 선택함
- ex) 지구 상에 존재하는 모든 친구 관계를 그래프로 표현한 후 Ash 와 Vanessa 사이에 존재하는 경로를 찾는 경우
- 공간 복잡도 : 공간을 얼마나 잡아 먹는지
2. Tree (트리)
- Tree란?
: 노드 간 부모 자식 관계를 가지는 (계층, 그룹의 개념이 있음) 계층적 자료구조
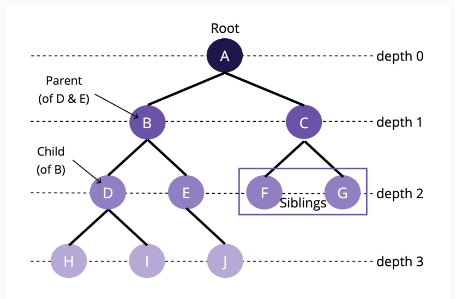
- 개념
- node : A, B, C, D 등 트리의 구성요소
- root : A처럼, 트리 구조에서 최상위에 존재하는 노드
- depth : 루트를 기준으로, 다른 노드로 접근하기 위한 거리
- sibling 관계 : 같은 부모를 가지면서, 같은 depth에 존재하는 노드들 (D와E & F와G)
- parent(부모)와 child(자식) : B와C(자식)의 A(부모)
- edge : 노드와 노드를 잇는 선 (방향은 위 -> 아래)
- leaf : 자식이 없는 맨 끝의 노드
- height : 루트 노드의 높이 or 동등하게 가장 깊은 노드의 깊이
- 트리구조는 재귀적
- 들어오는 곳은 하나고 나오는 곳은 여러개가 될 수 있음
- 탐색 방법
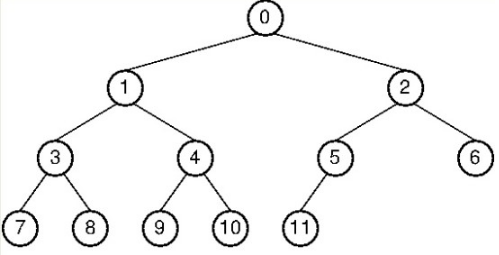
1) 전위 순회 (Preorder Traversal)
: 부모 → 좌 → 우 : 뿌리를 가장 먼저
0->1->3->7->8->4->9->10->2->5->11->6
2) 중위 순회 (Inorder Traversal)
: 좌 → 부모 → 우 : 좌측 하위 트리 방문 후 뿌리 방문
7->3->8->1->9->4->10->0->11->5->2->6
3) 후위 순회 (Postorder Traversal)
: 좌 → 우 → 부모 : 하위 트리 모두 방문 후 뿌리 방문
7->8->3->9->10->4->1->11->5->6->2->0
4) 층별 순회 (Level order Traversal)
: 위쪽 노드들부터 아래쪽으로 순차적으로 방문
0->1->2->3->4->5->6->7->8->9->10->11
2-1. Binary Tree (이진검색트리)
- Binary Tree란?
: 최대 2개의 자식만 갖는 트리 / 노드 값의 정렬 방법에 따라 순서가 존재
- 개념?
- 노드의 왼쪽 서브트리에는 노드의 값보다 작은 값이, 오른쪽 서브트리에는 노드의 값보다 같거나 큰 값이 존재 (<- 이 순서를 따르지 않는 트리는 Binary tree(이진트리)라고 함) /
- 종류
1) 정 이진 트리 (Full Binary Tree)
2) 완전 이진 트리 (Complete Binary Tree) : 모든 노드들이 레벨별로 왼쪽부터 채워져 있는 경우
3) 포화 이진 트리 (Perfect Binary Tree)
공간복잡도 시간복잡도 계속
