
💡문제
개똥벌레 한 마리가 장애물(석순과 종유석)로 가득찬 동굴에 들어갔다. 동굴의 길이는 N미터이고, 높이는 H미터이다. (N은 짝수) 첫 번째 장애물은 항상 석순이고, 그 다음에는 종유석과 석순이 번갈아가면서 등장한다.
아래 그림은 길이가 14미터이고 높이가 5미터인 동굴이다. (예제 그림)
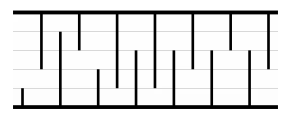
이 개똥벌레는 장애물을 피하지 않는다. 자신이 지나갈 구간을 정한 다음 일직선으로 지나가면서 만나는 모든 장애물을 파괴한다.
위의 그림에서 4번째 구간으로 개똥벌레가 날아간다면 파괴해야하는 장애물의 수는 총 여덟개이다. (4번째 구간은 길이가 3인 석순과 길이가 4인 석순의 중간지점을 말한다)
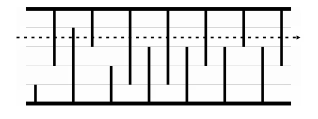
하지만, 첫 번째 구간이나 다섯 번째 구간으로 날아간다면 개똥벌레는 장애물 일곱개만 파괴하면 된다.
동굴의 크기와 높이, 모든 장애물의 크기가 주어진다. 이때, 개똥벌레가 파괴해야하는 장애물의 최솟값과 그러한 구간이 총 몇 개 있는지 구하는 프로그램을 작성하시오.
입력
첫째 줄에 N과 H가 주어진다. N은 항상 짝수이다. (2 ≤ N ≤ 200,000, 2 ≤ H ≤ 500,000)
다음 N개 줄에는 장애물의 크기가 순서대로 주어진다. 장애물의 크기는 H보다 작은 양수이다.
출력
첫째 줄에 개똥벌레가 파괴해야 하는 장애물의 최솟값과 그러한 구간의 수를 공백으로 구분하여 출력한다.
예제입력
6 7
1
5
3
3
5
1예제출력
2 3📖내가 작성한 Code
import sys
import collections
'''
imos 기법 문제
'''
def imos(N, H, obs):
stalagmite_differ_array = [0] * (H + 1)
stalactite_differ_array = [0] * (H + 1)
for i in range(N):
if i % 2 == 0:
stalagmite_differ_array[0] += 1
stalagmite_differ_array[obs[i]] -= 1
else:
stalactite_differ_array[H] += 1
stalactite_differ_array[H - obs[i]] -= 1
beak_stalagmite = [stalagmite_differ_array[0]] + [0] * (H - 1)
beak_stalactite = [0] * (H - 1) + [stalactite_differ_array[H]]
for i in range(1, H):
beak_stalagmite[i] = beak_stalagmite[i - 1] + stalagmite_differ_array[i]
beak_stalactite[H - i - 1] = beak_stalactite[H - i] + stalactite_differ_array[H - i]
result = collections.Counter([i+j for i, j in zip(beak_stalagmite, beak_stalactite)])
key = min(result.keys())
return key, result[key]
def main():
inputs = map(int, sys.stdin.read().split())
N, H = next(inputs), next(inputs)
obs = [next(inputs) for _ in range(N)]
sys.stdout.write(" ".join(map(str,imos(N, H, obs))))
if __name__ == '__main__':
main()
✍️풀이과정
imos 예시 문제라길래 풀어봄. index만 조심하면 될듯.
imos법(imos method 혹은 いもす法)
고안자 今城 健太郎 (Kentaro Imajo)씨의 닉네임인 imos의 이름이 유래된 방법으로, 누적합 알고리즘을 다차원, 다차수로 확장한 방법
길이가 N인 배열(혹은 리스트)이 있고, 𝑄번에 걸쳐 [l,r] 구간에 일정 값을 더하거나 빼야 하는 누적합의 경우 O(r−l+1)
차분 배열(Difference Array)이나 이벤트 기록(Event Recording) 기법을 사용하여, 구간의 시작점에는 더할 값을 더하고, 구간의 끝 지점 바로 다음에는 다시 그 값을 빼버리는 ‘표식’을 남기는 방법
업데이트 단계에서는 각 연산을 O(1)에 수행하고 마지막에 한번에 실행하므로 전체 시간 복잡도는 O(N+Q)
🧠 코드 리뷰
성능/정답/접근 모두 잘 되어 있는 코드입니다. 큰 수정 없이도 문제 해결은 충분하며, 소소한 리팩토링(주석, 변수명, Counter 생략 가능성) 정도 고려해 보시면 좋겠습니다.
🛠️AI 개선 코드
import sys
def imos_improved(N, H, obs):
# 하나의 차분 배열(difference array)만 사용
diff = [0] * (H + 1)
# N개의 장애물을 두 개씩 (석순/종유석) 처리
# 짝수 i -> 석순, 홀수 i -> 종유석
# 기존 '더 빠른' 코드에서도 활용된 로직과 동일
for i in range(0, N, 2):
# 석순(obs[i]) : H - obs[i] 위치부터 위로 +1
diff[H - obs[i]] += 1
# 종유석(obs[i+1]) : obs[i+1] 위치부터 위로 -1
diff[obs[i+1]] -= 1
# 현재 장애물 수(current)는 "N/2"로 시작
# 왜냐하면 N개 중 절반은 석순, 절반은 종유석인데,
# 가장 아래(또는 위) 기준에서 석순/종유석이 모두 영향을 주지 않은 상태를 0으로 보고
# diff를 올라가면서(또는 내려가면서) 실제 카운트를 구하는 방식
current = N // 2
min_stone = current
count = 1
# 1부터 H까지 누적합을 구하며 최소값 및 등장 횟수를 갱신
for h in range(1, H + 1):
current += diff[h]
if current < min_stone:
min_stone = current
count = 1
elif current == min_stone:
count += 1
return min_stone, count
def main():
input_data = sys.stdin.read().split()
N = int(input_data[0])
H = int(input_data[1])
obs = list(map(int, input_data[2:]))
min_val, cnt = imos_improved(N, H, obs)
print(min_val, cnt)
if __name__ == '__main__':
main()
💻결과

