1번. 중복 검사
- 배열을 정렬하면 현재 문자 다음에 오는 문자는 같거나 다르다.
- set을 이용하여 중복되는 문자인지 확인한다.
- hashset : Set 인터페이스에서 지원하는 구현 클래스
- Set + in = O(1) vs List + in = O(N)
- 중복되는 문자가 없다면 원래 리스트와 중복을 제거한 리스트의 길이는 같다.
2번. 아나그램
- 원래 문자열의 문자들을 모두 한 번씩 사용하여 단어 만들기
- 원래 문자열과 새로운 문자열을 정렬하면 같다.
- 주어진 문자열을 모두 사용하여 새로운 문자열을 만들어야 한다. 즉, 개수가 같다.
- 반례 : s와 t의 문자열 길이는 서로 다르다
3번. 배열 합치기
- list + list
- extend : 반환값이 없다.
4번. 오른쪽 가장 큰 요소로 바꾸기
- 뒤에서부터 저장해둔 최댓값과 비교하여 작은지 큰지 확인한다.
- 작으면 저장해둔 최댓값 / 크다면 저장해둔 최대값과 서로 바꾼다.
- 시간 초과(왼쪽부터 하면 최댓값을 계속 확인해야한다) : for + max()
5번. 해당 문자열의 하위 시퀀스
- while 문을 이용하여 두 문자열이 같은지 다른지 확인한다.
- 같으면 상위, 하위 다음 문자 / 다르다면 상위 다음 문자로 이동한다.
- 이중 for 문 : 만약 두 문자가 같다면 idx(내부 for문의 시작값)에 현재 인덱스 값 + 1
- 하위 시퀀스인지 판별하기 위해, 하위 시퀀스 길이만큼 visited 배열 생성
7번. 두 숫자의 합이 특정 숫자와 같은지 확인하기
- 특정 숫자에서 배열의 값을 뺀 나머지가 딕셔너리에 존재하는지 확인한다.
- 나머지가 없다면 딕셔너리에 저장 / 있다면 리턴한다.
- 반례 : 모든 숫자를 딕셔너리에 저장한 후 탐색한다면, 자기 자신을 또 반환할 수 있다. Ex) 6 - 3 = 3
8번. 문자열 배열 중에서 가장 긴 접두사 문자열 찾기
- 처음 문자열을 기준으로 각 문자열들의 문자들을 차례로 검사한다.
- 조건1 : 인덱스의 값이 각 문자열들의 길이와 같을 경우 종료
- 조건2 : 각 문자열들의 문자가 다를 경우 종료
- 만약 각 문자열 모두 같은 문자라면 저장해둔 접두사에 이어붙인다.
- 반례 : [""] / 배열의 길이 = 1, 문자열의 길이 = 0
9번. 그룹 아나그램
- 각 문자열들의 문자 개수를 알파벳 기준으로 계산하고, 딕셔너리에 해당 배열을 문자열로 저장한다.
- 딕셔너리는 배열을 저장할 수 없어 tuple로 저장한다.
- 즉, Key = 알파벳 기준 개수 배열 / Value = Key 값에 대한 문자열
- 반례 : 문자열의 전체 유니코드 값을 key로 설정할 때, 문자열이 다르지만 전체 유니코드 값이 같을 수 있다.
10번. 파스칼 삼각형
- [0] + 이전 숫자행 배열 + [0] 로 설정한 후 반복문을 수행한다.
- 다음 숫자행 배열의 길이는 이전 숫자행 배열의 마지막 값과 같다.
- 처음과 마지막 값은 무조건 1 / 나머지는 바로 위(이전 숫자행)에 있는 두 숫자의 합이다.
12번. 이메일 만들기
- 반례 : 로컬 이름과 도메인 이름을 구분해야 한다.
13번. 두 문자의 동형
- 함정 : s의 문자를 대체하여 t를 얻을 수 있으면 두 문자열 s와 t는 동형입니다.
- 반례 : s와 t가 동형이면, t의 문자를 대체하여 s를 얻을 수 있어야 한다.
Input: s = "badc", t = "baba"
Output: false14번. 인접하는 숫자 판단하기
- 문제점 : 양옆과 양옆 사이는 판별하는 기준이 다르다.
- 양옆과 양옆 사이의 판별 기준을 동일시 하기 위해 양 옆에 [0]을 추가한다.
- 인덱스 범위 해결 : for문의 인덱스를 1부터 n - 1까지 검사할 수 있다.
- 어렵게 풀기
- Ex01과 Ex02 = flowerbed가 같고 n이 다른 경우
- flowerbed = [1, 0, 0, 0, 1], n = 1 (True) vs n = 2 (False)
- 판단 1 : flowerbed가 다른 경우가 필요해보인다. (심은 꽃을 기준으로 테스트 케이스 추가하기)
- Ex03 : flowerbed = [1, 0, 0, 0, 0], n = 2
- Ex04 : flowerbed = [0, 0, 0, 0, 1], n = 2
- Ex05 : flowerbed = [0, 0, 0, 0, 0], n = 3
- 판단 2 : 화단에 새 꽃을 심을 수 있는 개수를 파악해보자.
- 판별 1 : (3 + 1) // 2 = 2 (X) (Ex01) vs (4 + 1) // 2 (O) (Ex03, Ex04, Ex05)
- Ex01의 심을 수 있는 개수를 맞추기 위해 필요한 기준을 선별하기에는 어려워보인다.
- 판별 2 : (3 - 1) // 2 = 1 (O) (Ex01) vs (4 - 1) // 2 (X) (Ex03, Ex04, Ex05)
- 판단 3 : Ex03, Ex04, Ex05의 심을 수 있는 개수를 맞추기 위해 다른 조건이 필요하다.
- 기준 1 : 맨 앞에 꽃이 심어져있는 경우 ➡︎ Ex01, Ex03 s Ex04, Ex05
empty = 0 if flowerbed[0] == 1 else 1
- 기준 2 : 맨 뒤에 꽃이 심어져있는 경우 ➡︎ Ex01, Ex04 vs Ex03, Ex05
n -= empty // 2
15번. 다수의 요소 반환하기
- 다수의 요소를 반환할 변수 res와 해당 요소(res)의 개수인 maxCount 변수를 이용한다.
- 딕셔너리에 저장된 변수의 개수를 기준으로 maxCount와 비교하여 다수의 요소를 선정한다.
- 반복문을 돌면서 요소가 같다면 count + 1 / 다르면 - 1, count가 0일 때 다수의 요소를 바꿔준다.
- 요소들의 개수를 딕셔너리에 저장하고 역순으로 정렬하여 다수의 요소를 반환한다.
16번. x의 다음 인덱스를 기준으로 큰 요소 찾기
-
nums1 요소들의 인덱스를 저정한 딕셔너리를 만든다.
- nums2에 대한 이중 for문으로 nums1의 해당 요소가 존재하면 이후에 큰 값을 찾아 배치한다.
-
nums2의 요소가 nums1에 존재한다면 스택에 추가하고, 스택에 저장된 값들은 자신보다 큰 값을 찾는다.
- 응용 : "배열에 있는 일부 요소 x의 다음으로 큰 요소는 동일한 배열에서 x의 오른쪽에 있는 처음으로 큰 요소입니다."
nums1 = [1,3,5,2,4]
nums2 = [6,5,4,3,7,2,1]
res = [-1,7,7,-1,7]17번. 피벗 찾기
- 내 방법 : 배열에 대한 인덱스를 기준으로 왼쪽과 오른쪽 요소들의 합계를 수시로 확인한다.
- 왼쪽 요소들의 합계와 오른쪽 요소들의 합계에 대한 변수를 이용한다.
- 오른쪽 요소들의 합계는 = 전체 - 해당 요소의 값 - 왼쪽 요소들의 합계
- 배열 = [1, 3, 2, 4, 5], idx = 2 -> 해당 요소의 값 = 2, 왼쪽 요소들의 합계 = 1 + 3
- 오른쪽 요소들의 합계는 = 전체 - 해당 요소의 값 - 왼쪽 요소들의 합계
18번. 해당 범위의 합계 구하기
- 처음부터 끝까지 인덱스를 기준으로 합계를 구한 배열을 생성한다. Ex) 2 ~ 6까지의 합계
- 해당 범위의 합계 = 0 ~ 6까지의 합계 - 0 ~ 1까지의 합계
- sum 함수 이용하기
19번. 해당 범위에서 포함되지 않은 요소들 찾기
- set + not in
- 배열의 인덱스를 이용하여 배열의 요소가 포함되는지 판단한다. (1 <= nums[i] <= n)
- 문제점 : [1, n] 범위
- 방법 : 배열에 특정 숫자가 존재한다면, 인덱스가 특정 숫자 - 1인 배열의 요소를 음수 처리한다.
- 단, 특정 숫자가 또 존재하더라도 -1을 유지해야 한다.
- 끝 : 음수인 요소들(해당 범위에 존재하는 nums의 요소들)을 확인한다.
20번. 단어의 개수 세기
- 내 방법 : 전체 텍스트의 문자들을 카운트하고, 단어에 포함되는 문자들의 개수만큼 빼주는 것을 반복한다.
- Counter 라이브러리를 이용하여 전체 텍스트와 단어에 해당하는 문자들의 개수로 나눈 몫을 이용한다.
- 즉, 만들 수 있는 단어의 개수는 해당 문자들 중에서 가장 작은 값이 된다.
21번. 문자열이 패턴과 동일한지 판단하기
- 반례 : pattern = "aaa", s = "aa aa aa aa"
- 반례 : pattern = "abba", s = "dog dog dog dog"
- b가 dog가 되지 않도록, 문자(dog)에 대한 패턴(a)을 저장하여 비교한다.
22번. HashSet 만들기
- 키가 0인 링크드 리스트(key=key, next=None)를 여러개 세팅한다.
- 여러개? : 충돌을 방지해야하고, 키 값만큼 세팅하는 것보다 작게 하는 것이 효율이 좋다.
- 세팅한 배열보다 큰 값들은? : 해당 키 값을 배열의 길이만큼 나눈 나머지에 위치시킨다.
- add 함수(키 값이 이미 존재하면 추가 안한다), remove 함수, contains 함수
- 해당 키 값을 찾을 때까지 탐색(while, cur = cur.next)하여 함수에 맞는 기능을 수행한다.
24번. 정렬 알고리즘
25번. 빈도수를 센 후 내림차순으로 출력하기
- 정수에 대한 빈도수를 세고, 빈도수를 정렬하기 위해 빈도수에 대한 정수 배열을 만든다.
- 빈도수가 같은 정수는 여러개이므로, 빈도수를 인덱스로 하여 정수들을 묶는다.
- 정수에 대한 빈도수를 세고, sorted lambda로 정렬한다.
26번. nums[i]를 제외한 nums의 모든 요소의 곱 구하기
- prefix과 postfix 배열을 만든 후, nums[i]를 기준으로 prefix의 왼쪽 값과 postfix의 오른쪽 값을 곱한다.
- prefix 배열 = nums[i](자기자신)와 prefix(이전 값들의 곱)으로 만든 배열
- postfix 배열 = prefix의 역순 방식
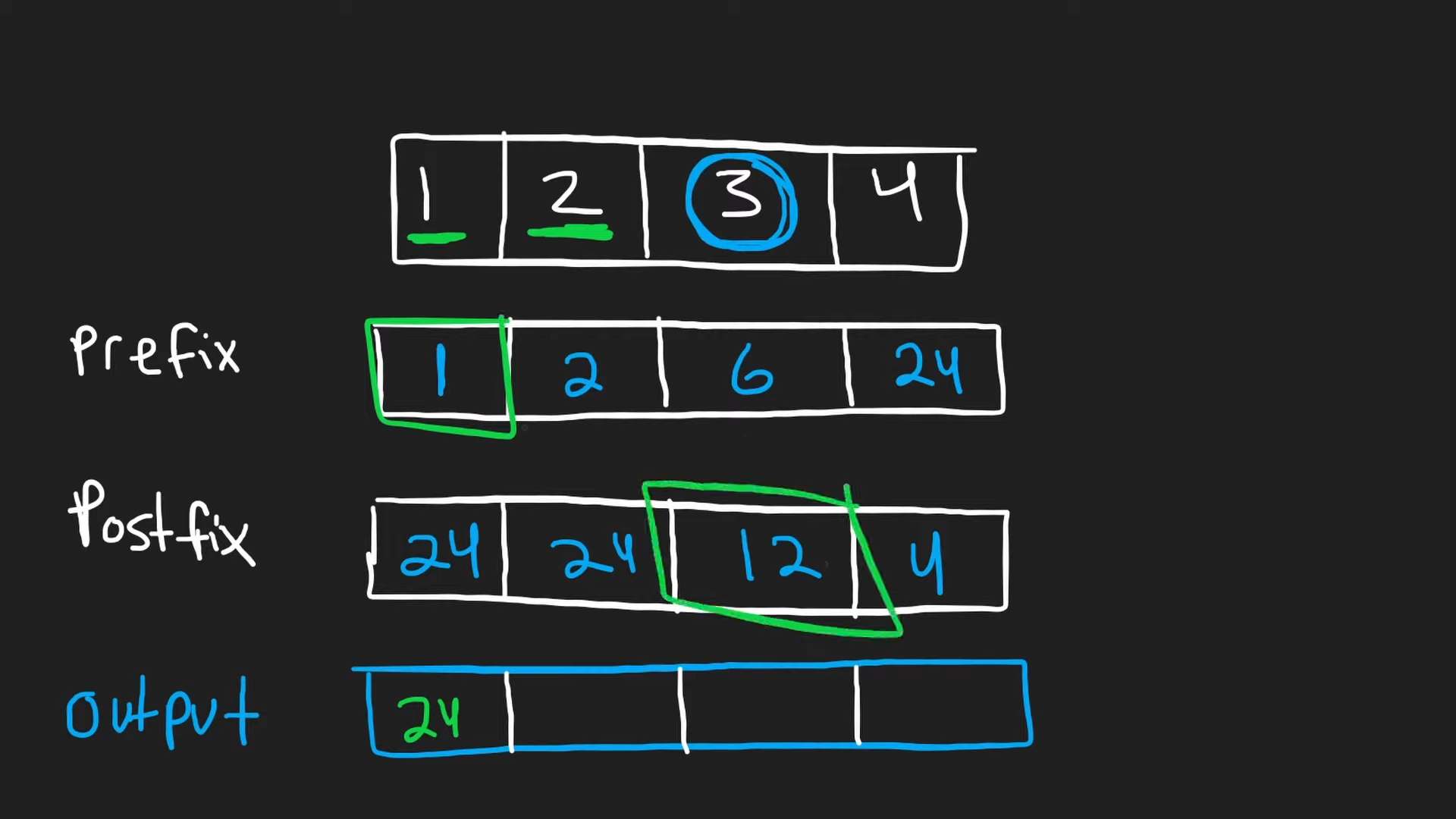
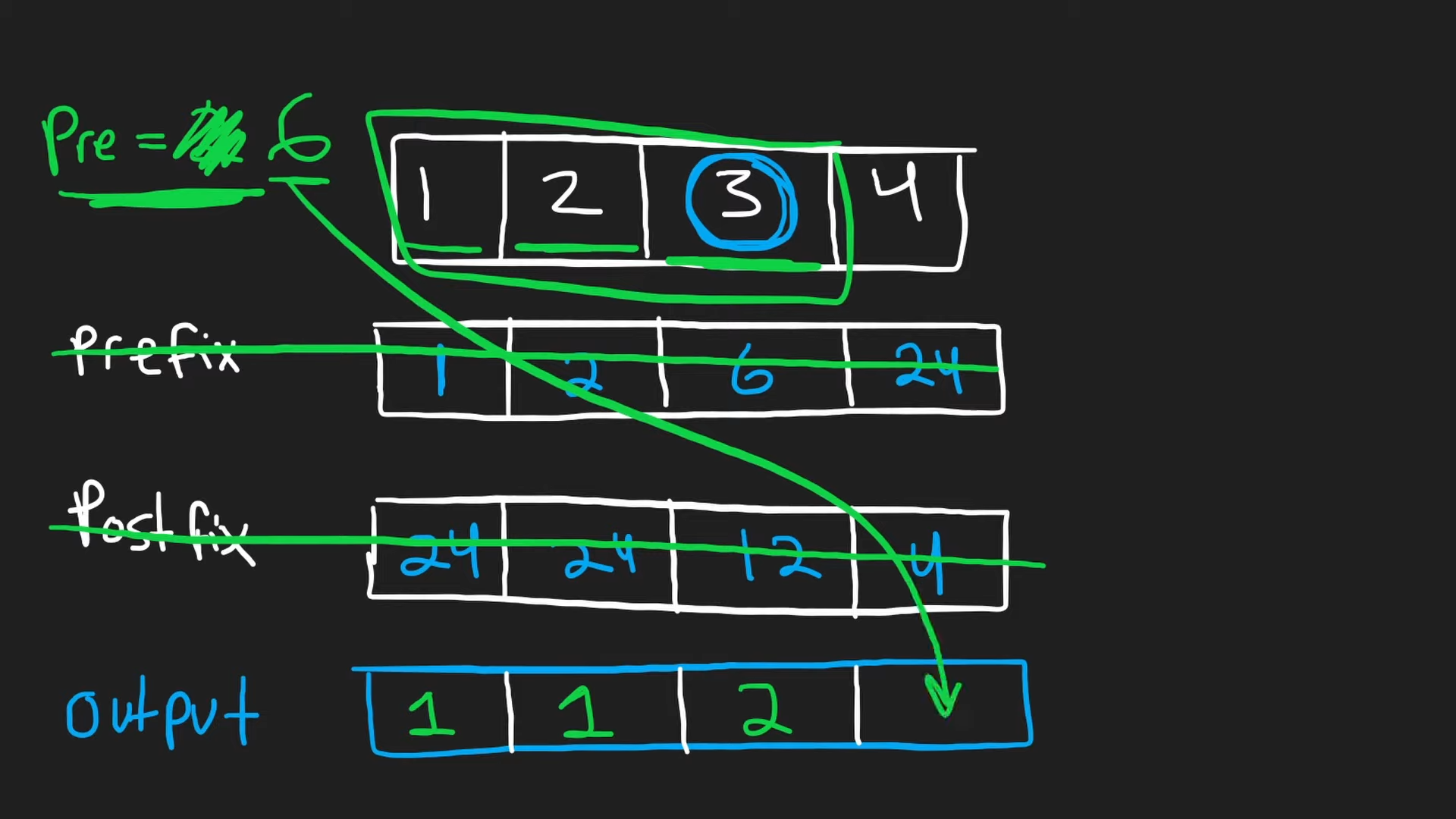
- 1번 방식과 달리 시작 지점에 1을 놓은 후, nums[i]와 이전 값들의 곱을 곱하여 prefix 배열을 만든다.
- 다음 postfix를 설정하기 위해 역순으로 처음에는 만들어진 prefix에 1을 곱하고, 나머지는 동일하다.
27번. 스도쿠
- 내 방법 : 검사 종류 3가지(열, 행, 3x3 사각형) + visited[False] * 10
- 3x3 사각형 : 쉽게 검사하기 위해, 해당 좌표가 어디든 0, 3, 6이 나올 수 있도록 한다.
- Ex) x = 4 ➡︎ dx = 4 // 3 * 3 = 3
- 3x3 사각형 : 쉽게 검사하기 위해, 해당 좌표가 어디든 0, 3, 6이 나올 수 있도록 한다.
- defaultdict(set) : set에서 in의 시간복잡도 = O(1)
- 3x3 사각형 : x = [0, 1, 2] y = [0, 1, 2]로 모든 경우의 수 = 9가지로 저장
28번. 특정 문자를 기준으로 분리하기(encode, decode)
- 내 방법(실패) : encode =
#을 각 문자열마다 추가하기, decode = split('#')을 나으로 분리하기- 반례 : ["we","yes","!@#$"] ➡︎
#은 내가 임의로 설정한 값이므로, 기존 문자열까지 건드리게 된다.
- 반례 : ["we","yes","!@#$"] ➡︎
- encode : 각 문자열 앞에 해당 문자열의 길이와
#을 추가한다. - decode : while 문으로
#을 찾아 encode에서 추가한 해당 문자열의 길이만큼 배열에 추가한다.- 주의 : 문자열의 길이는 1자리, 2자리, 3자리, ... 로 알 수 없다.
- i = 0 ➡︎ j =
#의 인덱스 값 ➡︎ i =#을 찾은 다음의 인덱스 값 + 해당 문자열의 길이
- i = 0 ➡︎ j =
- 주의 : 문자열의 길이는 1자리, 2자리, 3자리, ... 로 알 수 없다.
29번. 가장 긴 시퀀스의 길이
- 내 방법 : 배열을 정렬한 후 차례대로 검사한다. (단, 배열이 없으면 0)
- 검사 1 : 해당 값이 다음 값과 같다면 건너띈다.
- 검사 2 : 해당 값에 1을 더한 값이 다음 값과 같다면 시퀀스의 길이를 늘린다.
- 검사 3 : 만약 다르다면, 최대 시퀀스의 길이와 비교한 후, 시퀀스의 길이를 초기화한다.
- 마지막 : 검사 3에서만 최대 시퀀스 값이 바뀌기 때문에, 마지막에 해당 시퀀스의 길이를 한번더 비교한다.
- 중복을 제거한 배열에서 해당 값에 1을 뺀 값이 없다면, 반복문을 통해 시퀀스의 길이를 측정한다.
- Ex) [100, 4, 200, 1, 3, 2] ➡︎ 시각화하기 ← ..., 1, 2, 3, ... 100 ... 200 →
30번. 정렬
- 정렬하는 정수의 개수가 정해져 있을 때 Ex) 0, 1, 2
- 배열의 양 끝 값(l, r)을 저장한다.
- 현재 위치의 값이 0이라면, 정렬되지 않은 영역의 맨앞의 값(arr[l])과 자리를 바꾼다.
l += 1 - 현재 위치의 값이 2라면, 정렬되지 않은 영역의 맨뒤의 값(arr[r])과 자리를 바꾼다.
r -= 1i -= 1➡︎ 현재 위치의 값은 정렬된 상태가 아니기 때문에 다음으로 넘어갈 수 없다.
32번. 수직선 긋기
- 좌표 평면 위에서 수직선을 그엇을 때 교차된 벽돌의 개수를 최소화하기
- 내 방법(실패) : 수직선을 세울 수 있는 모든 공간의 교촤된 벽돌의 개수 파악하기
- 교차된 벽돌의 개수가 가장 적은 것 = 빈 공간의 개수가 가장 많은 것
- 문제점 : 공간이 비어있을 수 있음 Ex) [1]
- 교차된 벽돌의 개수가 없기 때문에 빈 배열에 해당 데이터를 미리 넣어준다.
dic = {0: 0}
- 교차된 벽돌의 개수가 없기 때문에 빈 배열에 해당 데이터를 미리 넣어준다.
- 문제점 : 공간이 비어있을 수 있음 Ex) [1]
34번. 합계가 k인 하위 배열의 총 개수 구하기
- 내 방법(실패) : 투 포인터 (+ nums의 원소는 양수이어야 한다)
- 반례 : [1], k = 0 ➡︎ nums의 원소와 k의 시작 범위가 같아야 한다.
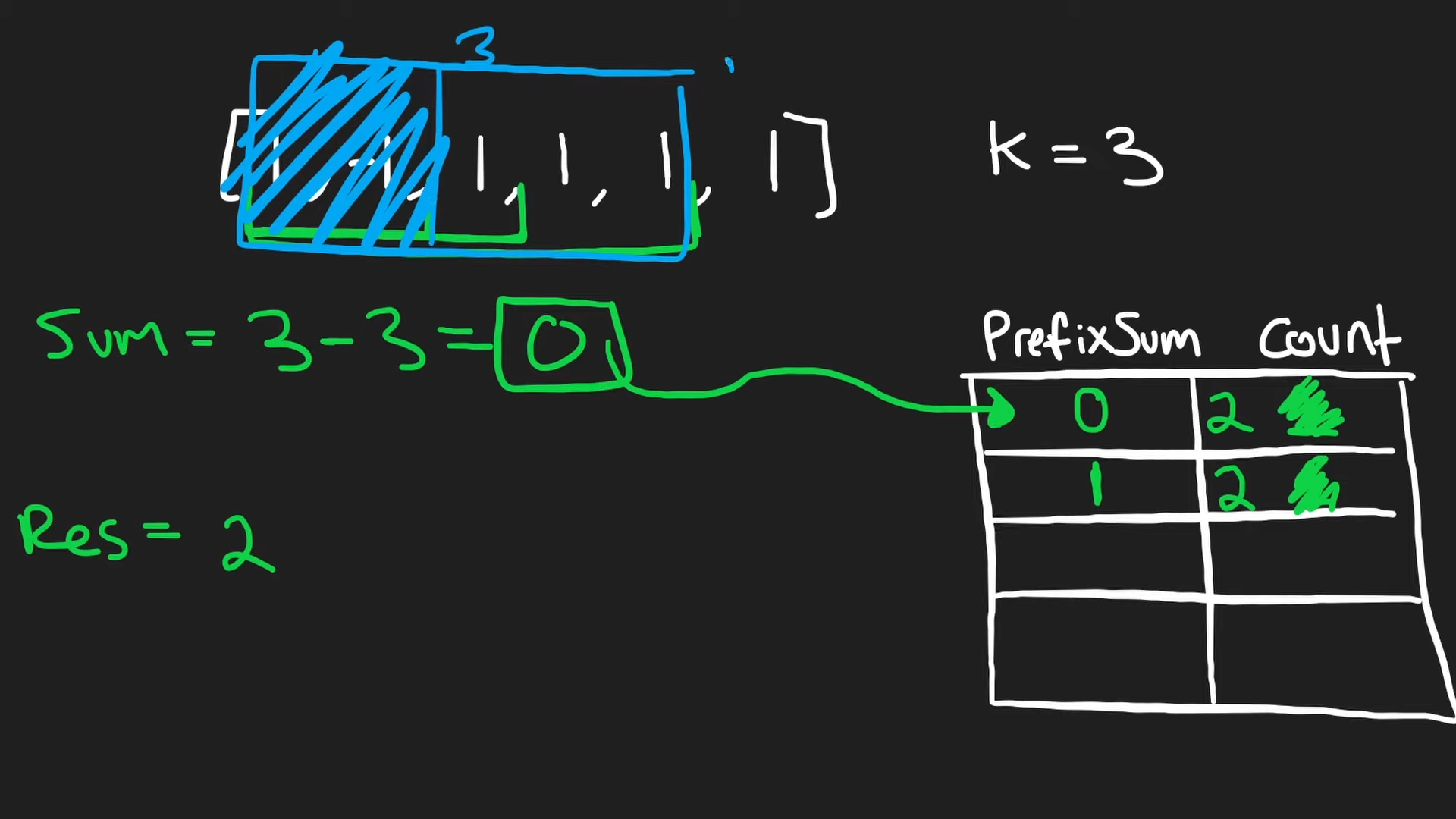
- 배열의 원소들을 더하면서 k만큼 뺀 나머지가 해쉬 맵에 존재하는지 확인한다.
- 해쉬 맵 : key = 특정 범위의 원소들의 합에서 k를 뺀 나머지 / value = 개수
- 해당 인덱스까지 나올 수 있는 모든 경우의 수의 합을 해쉬 맵에 저장해둔다.
- 초기 설정 : [10], k = 10 ➡︎ {0 : 1} res = 1
- 해당 인덱스까지 나올 수 있는 모든 경우의 수의 합을 해쉬 맵에 저장해둔다.
- 해쉬 맵 : key = 특정 범위의 원소들의 합에서 k를 뺀 나머지 / value = 개수
✅ 35번. 3자리 회문 개수 세기
- 왼쪽과 오른쪽에 대해 같은 문자가 존재할 경우, 그 사이에 존재하는 문자들은 모두 회문으로 만들 수 있다.
- s.find(c) vs list.index(c)
36번. 괄호 균형 맞추기
- Input: s = "] ] ] [ [ ["
- Output: 2 ➡︎ The resulting string is "[ [ ][ ] ]".
- Explanation: You can do the following to make the string balanced:
- Swap index 0 with index 4. s = "[ ] ] [ ]".
- Swap index 1 with index 5. s = "[ [ ][ ] ]". ➡︎ s = "[ ] [ ] ]"
- 설명 : 최소 스왑 수는 이미 균형을 이루는 괄호를 제외한 불균형을 이루는 괄호의 수에서 1을 더하고, 2를 나눈 값과 같다.
37번. 비율이 같은 직사각형 쌍의 개수
- 비율이 같은 직사각형이 몇개 있는지 카운트하고, 만들 수 있는 쌍의 개수 반환
- 만들 수 있는 쌍의 개수 = 중복을 허용하지 않고, n개의 원소에서 2개 뽑기 = nC2
✅ 38번. 두 개의 회문 subsequences(하위 시퀀스, 부분수열)
- 비트마스크를 이용하여 만들 수 있는 부분 수열을 구하고, 해당 부분 수열이 회문인지 확인하기
- 단, 두 개의 회문은 동일한 인덱스를 포함하면 안되므로, 비트연산자로 두 회문을 검사한다.
39번. 최적의 경로와 최대의 점수
- 첫번째 로봇이 마지막 위치까지 도달하려면, 첫번째 행에서 두번째 행으로 이동하는 경우가 존재한다.
- 교차지점을 기준으로 두번째 로봇이 얻을 수 있는 점수의 범위는 정해져있다.
- 각 행을 기준으로 prefix(특정 위치까지 모두 더한 값 vs postfix(반대로))를 계산한다.
- 전체 교차지점을 탐색하여, 첫번째 행과 두번째 행에서 얻을 수 있는 점수 중에서 최고 점수를 계산한다.
- 하지만, 첫번째 로봇이 점수를 최소화하기 때문에 답은 최저 점수가 된다.

40번. 전체 아나그램 개수
- 만들어야하는 아나그램의 길이만큼, 전체 문자열과 만들어야하는 아나그램에 대한 글자 수 세기
- 만약 두 그룹의 문자와 개수가 같다면, 첫번째 인덱스부터 아나그램을 만들 수 있다.
- 나머지 문자들을 확인하기 위해, 차례대로 문자(있거나 없을 수도 있음)를 추가하며, 맨 앞에 있는 문자를 빼준다.
- Ex) s = "cbaebabacd", p = "abc" ➡︎ ['c', 'b', 'a'] ➡︎ ['b', 'a', 'e']
- 새롭게 만들어진 문자열을 만들어야하는 아나그램과 비교한다.
✅ 41번. (KMP)Knuth-Morris-Pratt
- needle(바늘)과 haystack(건초 더미) : haystack = "ababcabcabababd", needle = "ababd"
- 기존 알고리즘에서는 needle을 찾을 때 다른 문자가 나왔을 경우, 다시 돌아가서 검사할때 중복되는 경우가 존재한다.
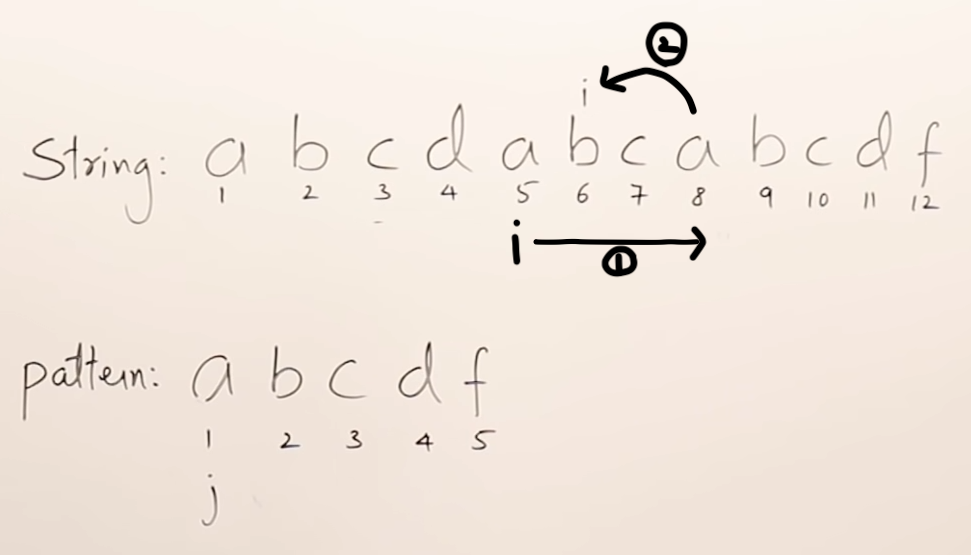
- needle에 대한 LPS(Longest Prefix Suffix)를 만든다. ➡︎ [0, 0, 1, 2, 0]
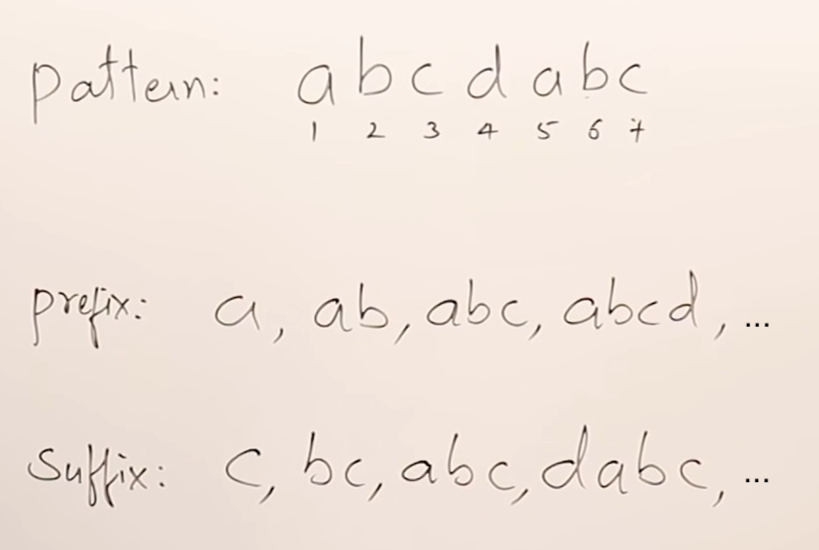
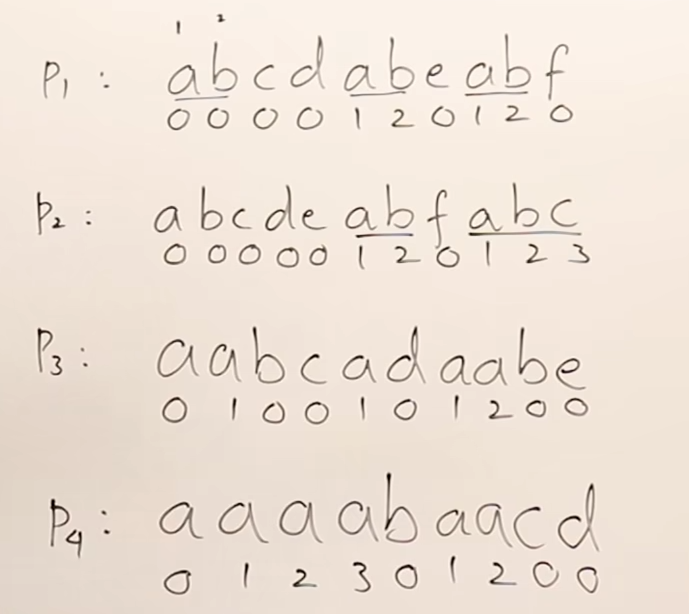 2. haystack와 needle을 비교하며, 다른 문자가 나왔을 경우, 다시 처음으로 돌아가는 것이 아닌 LPS의 값을 활용한다.
2. haystack와 needle을 비교하며, 다른 문자가 나왔을 경우, 다시 처음으로 돌아가는 것이 아닌 LPS의 값을 활용한다.
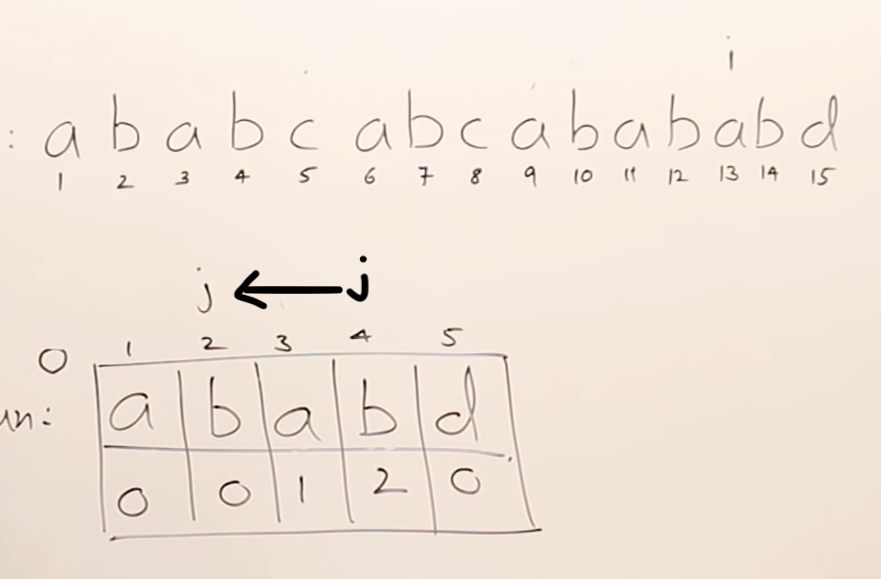
43번. Largest Number(functools.cmp_to_key)
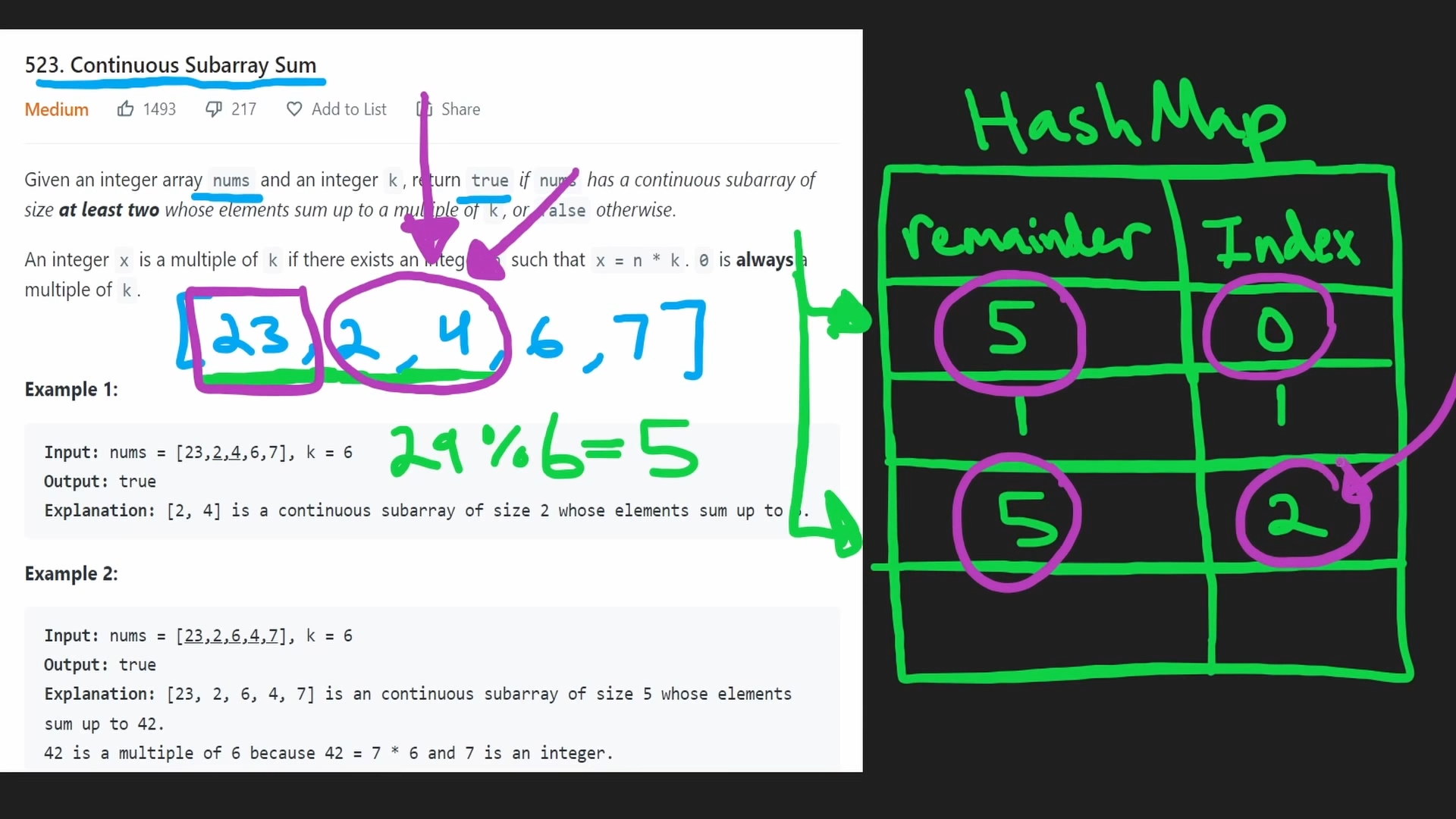
44번. 합계가 k의 배수인 하위 배열 찾기 (+34번)
- 배열의 원소들을 더하면서 k를 나눈 나머지가 해쉬 맵에 존재하는지 확인한다.
- 해쉬 맵 : key = 특정 범위의 원소들의 합에서 k를 나눈 나머지 / value = 하위 배열의 길이
- 초기 설정 : [24], k = 6 ➡︎ {0 : -1}, 하위 배열의 길이는 1보다 커야한다.
- 해쉬 맵 : key = 특정 범위의 원소들의 합에서 k를 나눈 나머지 / value = 하위 배열의 길이
48번. 길이 k의 모든 2진수가 s의 하위 문자열
- 공통 : 문자열 s에서 길이가 k인 나올 수 있는 모든 2진수를 문자열로 저장하기
- 내 방법 : 왼쪽 시프트 연산자(<<)를 이용하여 전체 2진수 확인하기
- 반례 : k = 3 ➡︎ 1 = 001 = '1'.zfill(k) == '1'.rjust(k, "0")
- Or : 문자열이 아닌 2진수를 저장하면, 정수형이라 더 비교하기 쉽다(0이 사라지기 때문에).
- 반례 : k = 3 ➡︎ 1 = 001 = '1'.zfill(k) == '1'.rjust(k, "0")
- 정답 : 길이 k가 가질 수 있는 모든 2진수의 개수 = 2 ** k
49번. 행과 열의 총합 구하기(2차원 배열, prefix)
- Rectangle[row2][col2] = (0, 0)에서 (row2, col2)까지의 총합
50번. 감소하지 않는 배열인지 판별하기(한 번 변경 가능)
- Ex01 : [4, 2, 3] ➡︎ 4를 2로 바꾸면(nums[i] = nums[i + 1]) 감소하지 않는 배열 가능 (핵심 : 기존 배열의 값 이용하기)
- Ex02 : [4, 2, 1] ➡︎ 4를 2로 바꾸기 [2, 2, 1]
- False ➡︎ [2, 2, 1]도 감소하는 배열이므로 끝까지 변경해보기 ➡︎ 1을 2로 바꾸면(nums[i + 1] = nums[i]) 가능
- 1차 : Ex01과 Ex02는 서로 바꿔주는 식이 다르다. ➡︎ 어떻게 구분해야할까?
- 차이점 : Ex01) i = 0 vs Ex02) i > 0 (핵심 : 바꿔야하는 값의 조건이 동일해야한다)
- 구분 : Ex01에서 i가 0보다 큰 경우로 맞춰주기 ➡︎ [1, 4, 2, 3] vs [2, 2, 1]
- 바꿔야하는 값 : Ex01-1) 4 vs Ex02) 1
- 결론 : 바꿔야하는 값의 양 옆 값[(1, 2), (2, 1)]을 기준으로 식이 적용된다.
✅ 51번. 19번 심화
- 배열에 존재하지 않는 가장 작은 양의 정수는 1부터 배열의 길이 사이의 정수 중 하나이다.
