제한 조건
- 풀이 시간 : 20분
- 시간 제한 : 1초
문제
행복 왕국의 왕실 정원은 체스판과 같은 8 × 8 좌표 평면이다. 왕실 정원의 특정한 한 칸에 나이트가 서있다. 나이트는 매우 충성스러운 신하로서 매일 무술을 연마한다. 나이트는 말을 타고 있기 때문에 이동을 할 때는 L자 형태로만 이동할 수 있으며 정원 밖으로는 나갈 수 없다. 나이트는 특정 위치에서 다음과 같은 2가지 경우로 이동할 수 있다.
- 수평으로 두 칸 이동한 뒤에 수직으로 한 칸 이동하기
- 수직으로 두 칸 이동한 뒤에 수평으로 한 칸 이동하기
이처럼 8 × 8 좌표 평면상에서 나이트의 위치가 주어졌을 때 나이트가 이동할 수 있는 경우의 수를 출력하는 프로그램을 작성하라. 왕실의 정원에서 행 위치를 표현할 때는 1부터 8로 표현하며, 열 위치를 표현할 때는 a 부터 h로 표현한다.
입력
- 첫째 줄에 8x8 좌표 평면상에서 현재 나이트가 위치한 곳의 좌표를 나타내는 두 문자로 구성된 문자열이 입력된다. 입력 문자는 a1 처럼 열과 행으로 이뤄진다.
출력
- 첫째 줄에 나이트가 이동할 수 있는 경우의 수를 출력하시오.
예시
| 입력 | 출력 |
|---|---|
| a1 | 2 |
| c2 | 6 |
풀이
나이트가 이동할 수 있는 경우의 수를 그려보면 다음과 같다.
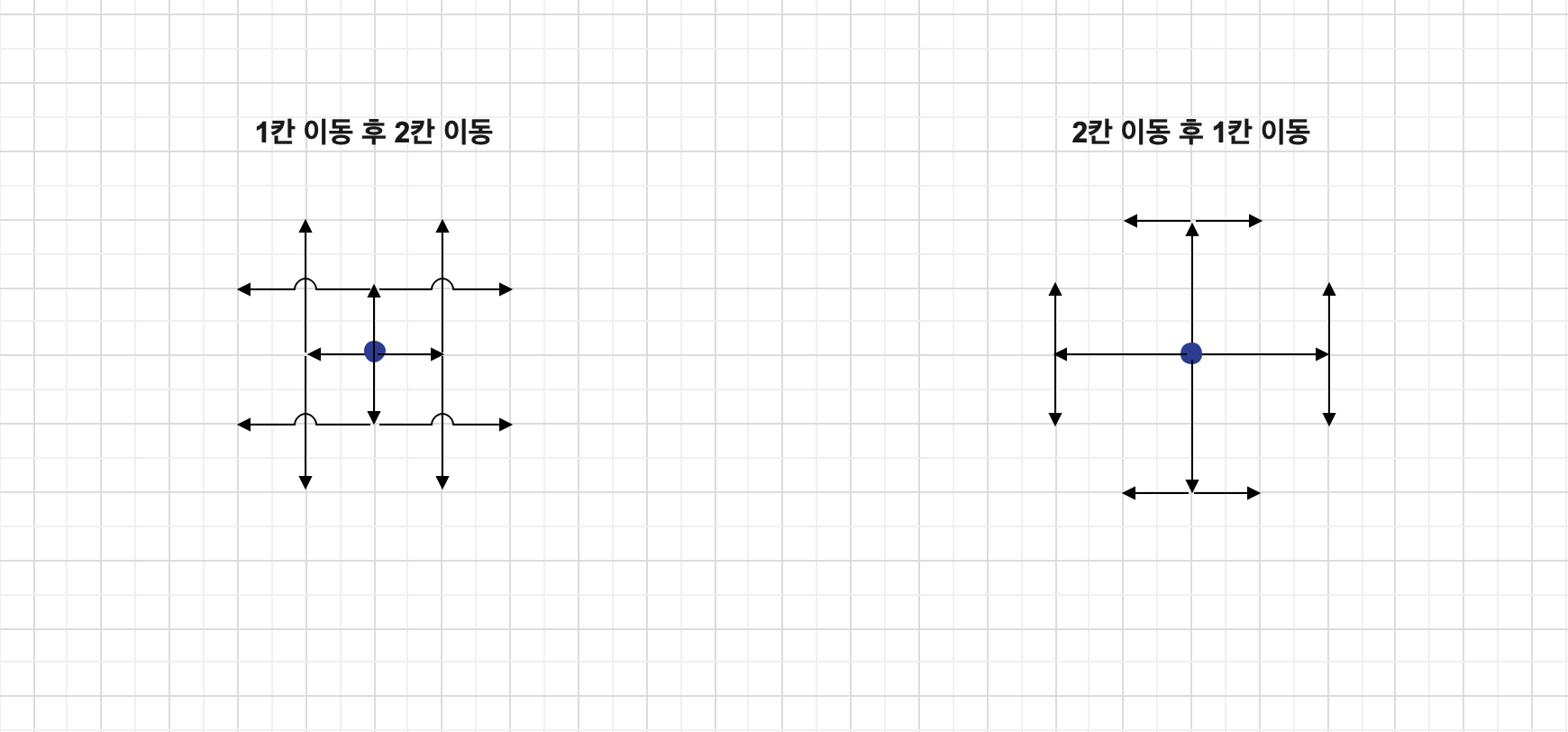
여기서 발생할 수 있는 좌표 이동을 작성해보면 다음과 같다.
(1, 2) (1, -2) (-1, 2) (-1, -2) (2, 1) (2, -1) (-2, 1) (-2, -1)나는 2가지 경우로 나눠서 생각했지만 좌표 이동으로 따져보니 사실은 동일한 이동이었다. 결과적으로 입력받은 좌표에 대해서 발생할 수 있는 경우의 수는 8개만 존재한다는 것이다.
즉, O(N)의 시간 복잡도로 연산해도 문제가 없으므로 입력 받은 좌표에 8개의 좌표 이동을 한 결과가 좌표 평면을 벗어났는지 확인만 하면 된다.
열 이동은 char 연산을 통해 a <= x <= h를 확인하고, 행 이동은 int 연산을 통해 1 <= y <= 8을 확인하여, 이 조건들을 충족하면 이동 가능한 경우의 수로 카운트하면 된다.
