해당 포스팅은 릿코드 617번 Merge Two Binary Trees 풀이를 다룬다. 문제 링크
코드는 javascript로 작성하였으며 DFS로 풀이하였다.

---

문제

You are given two binary trees root1 and root2.

Imagine that when you put one of them to cover the other, some nodes of the two trees are overlapped while the others are not. You need to merge the two trees into a new binary tree. The merge rule is that if two nodes overlap, then sum node values up as the new value of the merged node. Otherwise, the NOT null node will be used as the node of the new tree.

Return the merged tree.

Note: The merging process must start from the root nodes of both trees.

두 개의 이진트리 root1과 root2가 input으로 주어진다.
두 트리를 새로운 이진트리로 병합하라. 병합 규칙은 두 노드가 겹치면 노드 값을 합산하여 병합된 노드의 새 값으로 합산하는 것이다. 그렇지 않을 경우 null 노드가 새 트리의 노드로 사용된다.

이러한 규칙으로 병합된 트리를 반환하자. 병합은 두 트리의 루트 노드에서 시작해야 한다.

---

예제

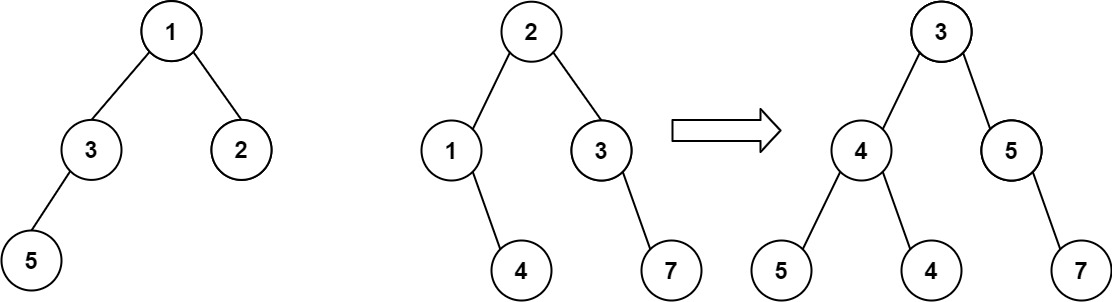
Input: root1 = [1,3,2,5], root2 = [2,1,3,null,4,null,7]
Output: [3,4,5,5,4,null,7]

---

풀이

root1과 root2의 각 노드(node.val)를 더해주자. 만약 둘 중 하나가 노드가 없을 시(val이 null) 다른 노드를 return 시켜준다.

두 노드를 더해주고 그 다음 left, right 노드를 더해주기 위해 DFS를 이용해 root1과 root2의 left, right에 대해 다시 재귀호출해주었다.

---

로직

root1과 root2 중 null인 것이 있을 시 다른 노드를 return 한다.
둘 중 하나라도 null일 시 더 이상 해당 root.val에 대해 left, right가 없으므로 각 root들의 left, right에 대해 재귀를 돌릴 필요가 없다.

if (!root1) {
  return root2;
}
if (!root2) {
  return root1;
}

트리를 병합하기 위해 두 노드를 더해준다.

root1.val += root2.val;

해당 노드의 left와 right를 더해준다. 모든 level의 노드들을 병합하기 위해 재귀호출한다.

root1.left = mergeTrees(root1.left, root2.left);
root1.right = mergeTrees(root1.right, root2.right);

---

전체 코드

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root1
 * @param {TreeNode} root2
 * @return {TreeNode}
 */
var mergeTrees = function(root1, root2) {
    if (!root1) {
        return root2;
    }
    if (!root2) {
        return root1;
    }
    
    root1.val += root2.val;
    root1.left = mergeTrees(root1.left, root2.left);
    root1.right = mergeTrees(root1.right, root2.right);
    
    return root1;
};