[ch4 완전탐색] 멘토링 javascript

해당 포스팅은 인프런의 "자바스크립트 알고리즘 문제풀이" 강의 중 챕터4의 멘토링 문제 풀이를 다룬다. 완전탐색으로 풀이하였다.

---

문제

1. 문제 설명

• M번의 수학 테스트 등수를 가지고 멘토 멘티를 정한다
• 만약 A학생이 멘토이고 B학생이 멘티가 되는 짝이 되었다면, A학생은 M번의 수학테스트에서 모두 B학생보다 등수가 앞서야 한다.
• M번의 수학 성적이 주어지면 멘토와 멘티가 되는 짝을 만들 수 있는 경우가 총 몇 가지인지 출력하라

2. 입출력

INPUT:

• [첫 번째 줄] 반 학생 수(N) 시험 횟수(M)
• [2 ~ N + 1번째 줄] 테스트 결과

OUTPUT: 짝을 만들 수 있는 총 경우의 수

---

문제 추론

요구사항

(멘토-멘티) 짝이 되기 위해서는 모든 테스트에 대해 멘토가 멘티보다 앞에 있어야 한다.
이는 모든 테스트 결과에서 멘토 index가 멘티 index보다 더 작아야 한다는 의미이다.

풀이 방법

1. 가능한 모든 순서쌍([멘토, 멘티]을 만든 다음,
2. 각 순서쌍에 대해, 멘토가 모든 테스트에서 멘티보다 앞서는지 판별한다.
   모든 테스트에서 멘토-멘티 순서가 뒤바뀌지 않는다면 총 경우를 +1 해준다.

주의

가능한 모든 멘토-멘티 순서쌍은 4 * 4 = 16쌍이다.

[1,1], [1,2], [1,3], [1,4]
[2,1], [2,2], [2,3], [2,4]
[3,1], [3,2], [3,3], [3,4]
[4,1], [4,2], [4,3], [4,4]

이 때 [1,1] 처럼 멘토, 멘티 학생이 겹치는 경우가 있다.
이를 처리하기 위해 멘토 index ≥ 멘티 index로 순서를 비교해주자!

---

Pseudocode

function solution(arr) {
	가능한 순서쌍을 모두 만든다.
	cnt = 0;
	// ex. [1,2]
	for ([prev, next] of 순서쌍) {
		isPossible = true;
		for (array of arr) {
				// arr의 배열들을 돌면서 해당 순서쌍에서 하나라도 순서가 다를시
				if (array에서 prev 인덱스 >= next 인덱스) {
					isPossible = false;
					break;
				}
		}
		// 해당 순서쌍이 모든 경우에서 순서가 맞다면
		if (isPossible) ++cnt;
	}
	return cnt;
}

---

내 풀이

const input = require('fs').readFileSync('/dev/stdin').toString().split('\n').slice(0, -1);
const [n,m] = input.shift();
const tests = input.map(line => line.split(" ").map(el => Number(el)));

const pair = [];
for (let i=1; i<=n; i++) {
    for (let j=1; j<=n; j++) {
        pair.push([i,j]);
    }
}

let cnt = 0;
for (const [mento, menti] of pair) {
    let isPossible = true;
    for (const test of tests) {
        const mentoIdx = test.indexOf(mento);
        const mentiIdx = test.indexOf(menti);
        if (mentoIdx >= mentiIdx) {
            isPossible = false;
            break;
        }
    }
    if (isPossible) cnt++;
}

console.log(cnt)

시간복잡도: $O(MN^3)$

---

Solution

멘토-멘티 쌍을 (i, j)라고 생각하자.

• 각 테스트 결과를 돌면서, i와 j의 인덱스 위치를 비교한다음,
• i < j라면 cnt++를 하며, (만약 해당 테스트에서 멘토 index< 멘티 index일 시 cnt++)
• 테스트 loop가 종료될 때 cnt === 시험횟수(m)라면 해당 순서쌍은
  모든 테스트에서 멘토가 멘티보다 등수가 앞선다.
  따라서 해당 순서쌍은 멘토-멘티가 될 수 있으므로 answer++한다.

function solution(test) {
  let answer = 0;
  const m = test.length;
  const n = test[0].length;
  
  for (let i = 1; i <= n; i++) {
    for (let j = 1; j <= n; j++) {
      let cnt = 0;
      for (let k = 0; k < m; k++) {
        let pi = pj = 0;
        for (let s = 0; s < n; s++) {
          if (test[k][s] === i) pi = s;
          if (test[k][s] === j) pj = s;
        }
        if (pi < pj) cnt++;
      }
      if (cnt === m) answer++;
    }
  }
  return answer;
}

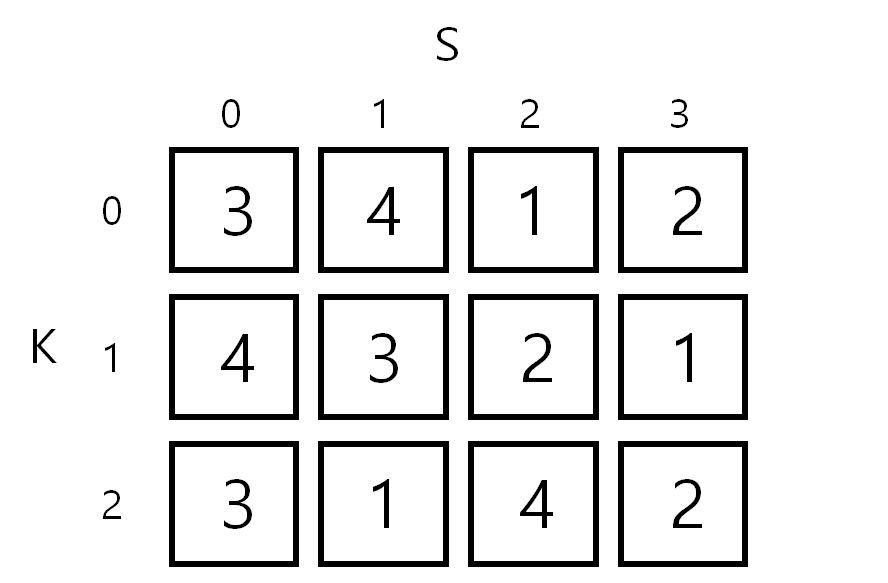
let arr=[[3, 4, 1, 2], [4, 3, 2, 1], [3, 1, 4, 2]];
console.log(solution(arr));