해당 포스팅은 백준 2187번 미로탐색 풀이를 다룬다. 문제 링크
코드는 javascript로 작성하였으며 BFS로 풀이하였다.

---

풀이

바킹독님의 풀이를 보고 풀었다.

"최단경로 찾기" 문제이므로 BFS로 풀이해야 한다.

DFS는 처음으로 발견되는 해답이 최단거리임을 보장할 수 없으므로 최단거리를 찾기 위해 완전탐색한 후 그 중에서 최솟값을 구한다. 따라서 가지가 많을 경우 시간초과가 난다.

반면 BFS는 현재 노드에서 가까운 노드부터 찾기 때문에 경로 탐색 시 첫 번째로 찾아지는 해답이 곧 최단거리다.

---

로직 설명 - BFS를 이용한 최단 거리 측정

좌표 (0,0)에서 (N-1,M-1)까지 도착하기 위해 BFS를 돈다. 파란 상자는 1(이동할 수 있는 칸) 빨간 상자는 0(이동할 수 없는 칸)이라고 가정하자.

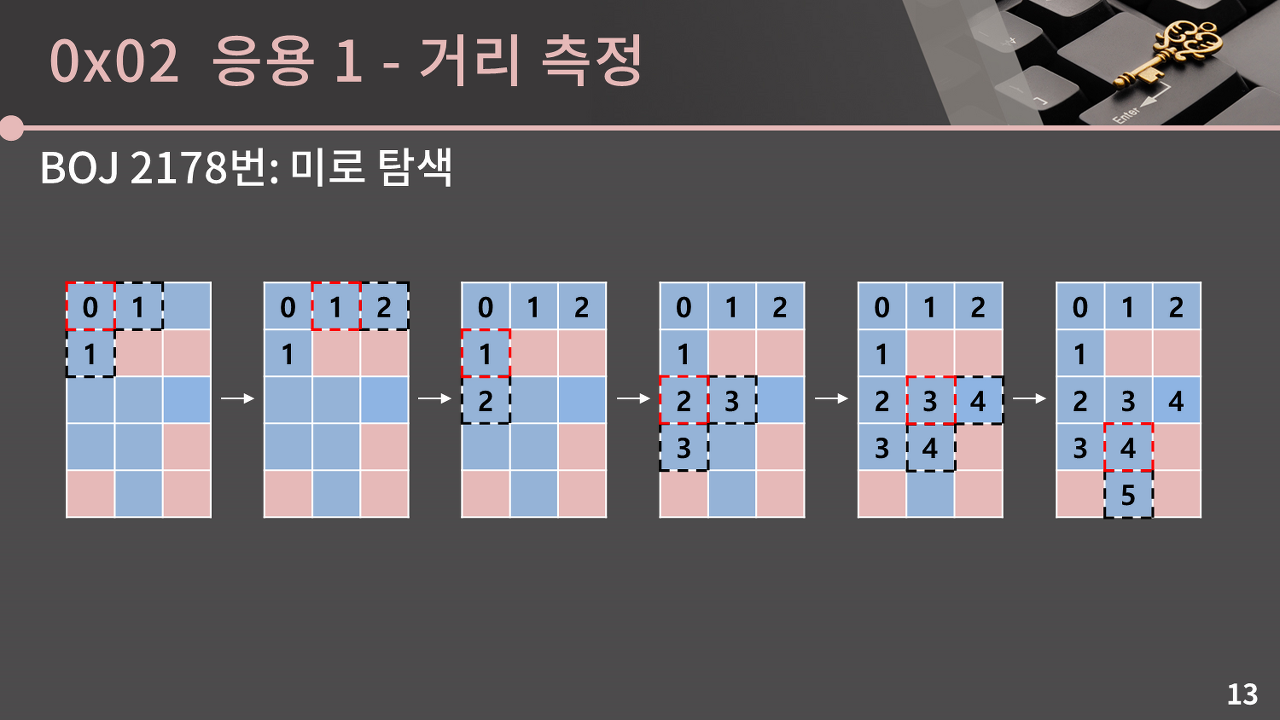
각 칸들에 (0,0)까지의 거리를 적어두면 위의 사진과 같다. 빨간색 점선은 현재 보는 칸이고, 검정색 점선은 추가되는 칸인데, 현재 보고 있는 칸으로부터 추가되는 인접한 칸은 거리가 현재 보는 칸보다 1만큼 더 떨어져있다.

제일 첫 번째는 빨간색 점선에서 거리가 0인데 검정색 점선에서 거리가 1이고, 마지막껀 빨간색 점선에서 거리가 4인데 검정색 점선에서는 거리가 5이다. 이 성질을 활용하면 우리는 단순히 상하좌우로 연결된 칸들을 방문하는 것에서 끝나는 것이 아니라, 시작점과의 거리를 전부 계산할 수 있다.

---

코드 설명

• dist : BFS를 돌리기 전에 배열 dist를 배열 크기만큼 -1로 채워주자. dist는 노드 방문을 체크하는 visited와 최단경로를 구하는 역할을 할 것이다.
• dist[0][0] : 좌표 (0,0)에 대해 0으로 업데이트한다. 최단경로를 구하기 위해 방문하는 맨 처음 노드이기 때문이다.

const dist = [...Array(r)].map(() => Array(c).fill(-1));
dist[0][0] = 0;

• cnt : 방문한 노드 개수를 저장

let cnt = 0;

• if (cell === 0 || dist[i][j] > 0) continue : 배열에 대해 loop를 돌리면서 좌표값이 0이거나(이동할 수 없는 칸) 이미 방문한 노드일 경우(dist[i][j]가 양수인 경우) continue
• queue.push([i,j,dist[i][j]]) : 이외에는 방문해야 하는 노드이므로 큐에 좌표값(i,j)과 현재 경로까지의 값(dist[i][j]) 삽입

for (let i=0; i<r; i++) {
  for (let j=0; j<c; j++) {
    const cell = board[i][j];
    if (cell === 0 || dist[i][j] > 0) continue;
    queue.push([i,j,dist[i][j]]);
    
    ...
    
  }
}

• BFS를 돌리면서 현재 좌표값의 상하좌우에 방문할 수 있는 원소가 있을 시,
  • dist[nx][ny] = cnt + 1 : 이전 좌표값에서 +1을 한 다음
  • queue.push([nx,ny,dist[nx][ny]]) : queue에 삽입한다

for (let i=0; i<r; i++) {
  for (let j=0; j<c; j++) {
    
    ...
    
    while(queue.length) {
      const [x, y, cnt] = queue.shift();
      for (let k=0; k<4; k++) {
        const nx = x + dx[k];
        const ny = y + dy[k];
        if (nx < 0 || ny < 0 || nx >= r || ny >= c) continue;
        if (dist[nx][ny] >= 0 || board[nx][ny] !== 1) continue;
        dist[nx][ny] = cnt + 1;
        queue.push([nx,ny,dist[nx][ny]]);
      }
    }
  }
}

---

전체 코드

const input = require('fs').readFileSync('/dev/stdin').toString().split('\n').slice(0,-1);
const NM = input.shift().split(" ");
const [r,c] = NM.map(el => Number(el));
const board = input.map(s => s.split("").map(el => Number(el)));

const dx=[1, 0, -1, 0];
const dy=[0, 1, 0, -1];

function solution(r,c,board) {
    const queue = [];
    const dist = [...Array(r)].map(() => Array(c).fill(-1));
    dist[0][0] = 0;
    
    let cnt = 0;
    for (let i=0; i<r; i++) {
        for (let j=0; j<c; j++) {
            const cell = board[i][j];
            if (cell === 0 || dist[i][j] > 0) continue;
            queue.push([i,j,dist[i][j]]);
            while(queue.length) {
                const [x, y, cnt] = queue.shift();
                for (let k=0; k<4; k++) {
                    const nx = x + dx[k];
                    const ny = y + dy[k];
                    if (nx < 0 || ny < 0 || nx >= r || ny >= c) continue;
                    if (dist[nx][ny] >= 0 || board[nx][ny] !== 1) continue;
                    dist[nx][ny] = cnt + 1;
                    queue.push([nx,ny,dist[nx][ny]]);
                }
            }
        }
    }
    return dist[r-1][c-1] + 1;
}

console.log(solution(r,c,board));

---

(ref) 바킹독님의 풀이