해당 포스팅은 백준 2583번 영역구하기 풀이를 다룬다. 문제 링크
코드는 Javascript로 작성하였다.
문제
문제 설명
눈금의 간격이 1인 M×N(M,N≤100)크기의 모눈종이가 있다. 이 모눈종이 위에 눈금에 맞추어 K개의 직사각형을 그릴 때, 이들 K개의 직사각형의 내부를 제외한 나머지 부분이 몇 개의 분리된 영역으로 나누어진다.
예를 들어 M=5, N=7 인 모눈종이 위에 <그림 1>과 같이 직사각형 3개를 그렸다면, 그 나머지 영역은 <그림 2>와 같이 3개의 분리된 영역으로 나누어지게 된다.
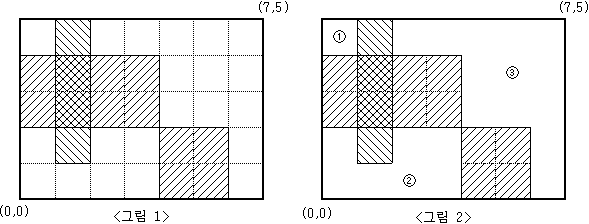
<그림 2>와 같이 분리된 세 영역의 넓이는 각각 1, 7, 13이 된다.
M, N과 K 그리고 K개의 직사각형의 좌표가 주어질 때, K개의 직사각형 내부를 제외한 나머지 부분이 몇 개의 분리된 영역으로 나누어지는지, 그리고 분리된 각 영역의 넓이가 얼마인지를 구하여 이를 출력하는 프로그램을 작성하시오.
입력
첫째 줄에 M과 N, 그리고 K가 빈칸을 사이에 두고 차례로 주어진다. M, N, K는 모두 100 이하의 자연수이다. 둘째 줄부터 K개의 줄에는 한 줄에 하나씩 직사각형의 왼쪽 아래 꼭짓점의 x, y좌표값과 오른쪽 위 꼭짓점의 x, y좌표값이 빈칸을 사이에 두고 차례로 주어진다. 모눈종이의 왼쪽 아래 꼭짓점의 좌표는 (0,0)이고, 오른쪽 위 꼭짓점의 좌표는(N,M)이다. 입력되는 K개의 직사각형들이 모눈종이 전체를 채우는 경우는 없다.
출력
첫째 줄에 분리되어 나누어지는 영역의 개수를 출력한다. 둘째 줄에는 각 영역의 넓이를 오름차순으로 정렬하여 빈칸을 사이에 두고 출력한다.
풀이
해당 문제는 문제에서 주어진 <그림1>을 회전한다음 input의 좌표값을 받아 인접행렬을 만든 다음 dfs로 풀이해야 하는 문제이다.
예제를 통해 로직을 자세하게 설명하겠다.
로직 & 예제 설명
문제의 예제1을 통해 자세한 로직을 설명하겠다.
위의 예제의 input을 파싱하면 다음과 같다.
- 가로 M: 5
- 세로 N: 7
- area: [
[0 2 4 4],
[1 1 2 5],
[4 0 6 2]
]
우리는 그림17x5처럼 NxM 가 아닌 5x7로(MxN) 인접행렬을 구현할 것이므로 M은 가로, N은 세로로 한다.
그다음 graph와 visted를 Array[M][N]으로 초기화한다. graph는 인접행렬을, visited는 area의 방문 여부를 판별할 것이다.
아래 사진은 <그림1>을 오른쪽으로 90도 회전했을 때 모습이다.
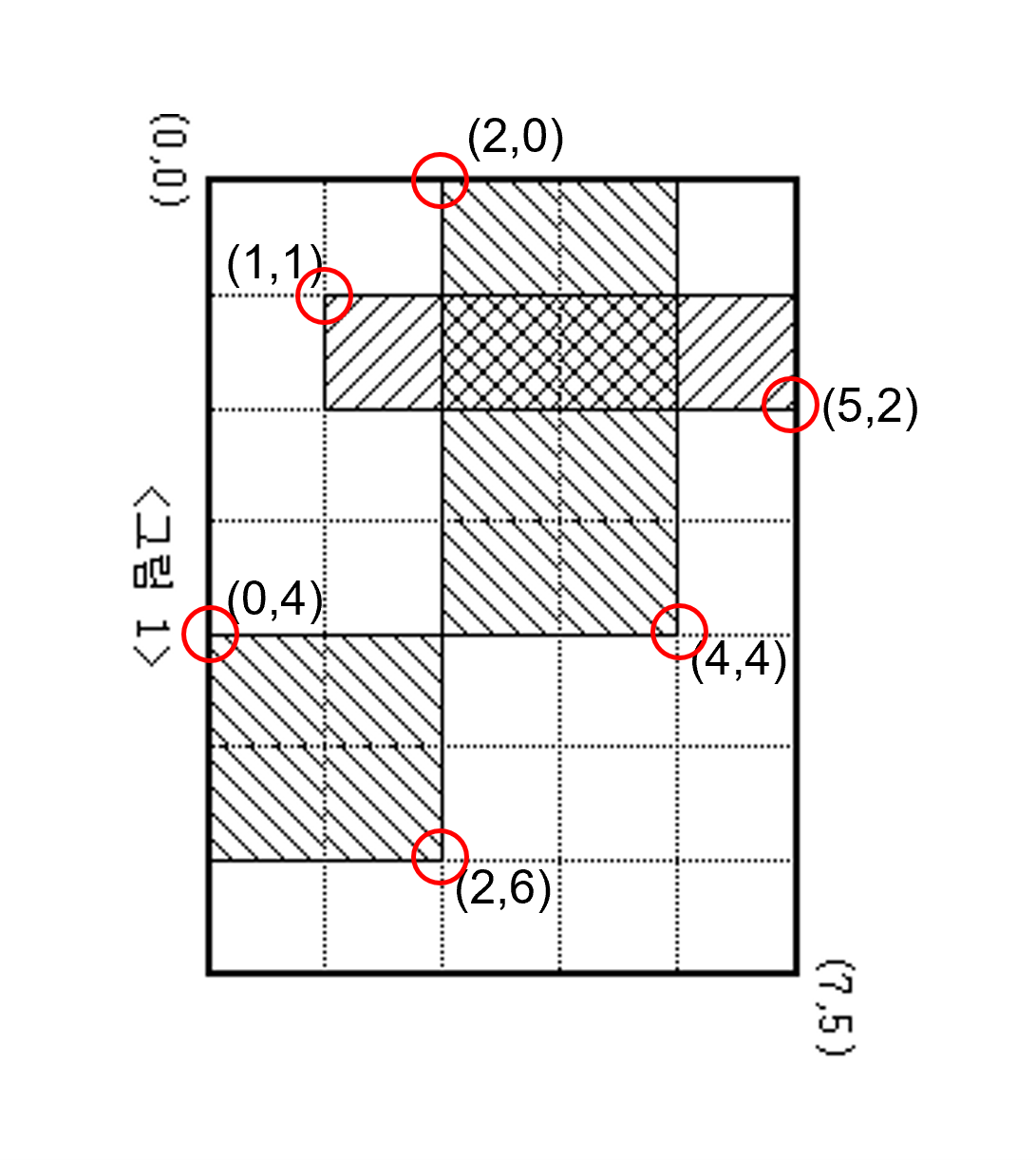
위 사진을 보면 좌표 x,y의 위치가 변경된 것을 확인할 수 있다. 예컨대 좌표 (0,2)는 (2,0)이다. 따라서 이를 유의하고 직사각형의 내부를 1로 해야한다. 또한 직사각형의 내부는 방문할 수 없는 점이므로, visited에서 각각의 값을 true로 해준다.
이를 코드로 옮기면 다음과 같다.
const area = [];
for (let i=0; i<K; i++) {
const arr = rect[i].map(el => Number(el));
const [x1,y1, x2,y2] = arr;
for (let j=x1; j<x2; j++) {
for (let k=y1; k<y2; k++) {
graph[j][k] = 1;
visited[j][k] = true;
}
}
}
그 다음 직사각형 내부를 제외한 나머지부분의 넓이를 구해야 한다. 넓이를 구하기 위해 변수 cnt를 0으로 초기화 한 다음, graph의 값이 0이고 방문하지 않은 원소에 대해 dfs한다.
for (let i=0; i<M; i++) {
for (let j=0; j<N; j++) {
if (graph[i][j] === 0 && !visited[i][j]) {
cnt = 0;
dfs(i,j);
area.push(cnt);
}
}
}dfs 함수에서는 해당 원소를 방문처리 하고 cnt를 +=1 한다. 그 다음 해당 원소의 상하좌우가 방문하지 않은 원소일 시, 그 원소를 다시 dfs한다.
더 이상 주변에 방문하지 않은 원소가 없을 시 dfs를 종료하게 된다. 종료하게 되면 cnt는 해당 분리된 영역의 넓이가 된다. 따라서 cnt를 area에 넣는다.
const dx=[-1, 0, 1, 0];
const dy=[0, 1, 0, -1];
function dfs(x,y) {
visited[x][y] = true;
cnt++
for (let k=0; k<4; k++) {
const nx = x + dx[k];
const ny = y + dy[k];
if (nx >= 0 && ny >= 0 && nx < M && ny < N && !visited[nx][ny] && graph[nx][ny] !== 1) {
dfs(nx, ny)
}
}
}
...
for (let i=0; i<M; i++) {
for (let j=0; j<N; j++) {
if (graph[i][j] === 0 && !visited[i][j]) {
cnt = 0;
dfs(i,j);
area.push(cnt);
}
}
}문제에서 첫 번째 줄에는 영역의 개수를, 둘 째 줄에는 각 영역의 넓이를 오름차순 정렬해서 출력하라고 나와있으므로 그에 맞추어 출력해주면 된다.
const sorted_area = area.sort((a,b) => a-b);
const area_cnt = area.length;
console.log(area_cnt);
console.log(sorted_area.join(" "));전체 코드
const input = require('fs').readFileSync('/dev/stdin').toString().split('\n').slice(0, -1);
const NMK = input.shift().split(" ");
const [N, M, K] = NMK.map(el => Number(el));
const rect = input.map(el => el.split(" "));
const graph = new Array(M).fill(0).map(() => new Array(N).fill(0));
const visited = new Array(M).fill(false).map(() => new Array(N).fill(false));
let cnt;
const area = [];
const dx=[-1, 0, 1, 0];
const dy=[0, 1, 0, -1];
function dfs(x,y) {
visited[x][y] = true;
cnt++
for (let k=0; k<4; k++) {
const nx = x + dx[k];
const ny = y + dy[k];
if (nx >= 0 && ny >= 0 && nx < M && ny < N && !visited[nx][ny] && graph[nx][ny] !== 1) {
dfs(nx, ny)
}
}
}
for (let i=0; i<K; i++) {
const arr = rect[i].map(el => Number(el));
const [x1,y1, x2,y2] = arr;
for (let j=x1; j<x2; j++) {
for (let k=y1; k<y2; k++) {
graph[j][k] = 1;
visited[j][k] = true;
}
}
}
for (let i=0; i<M; i++) {
for (let j=0; j<N; j++) {
if (graph[i][j] === 0 && !visited[i][j]) {
cnt = 0;
dfs(i,j);
area.push(cnt);
}
}
}
const sorted_area = area.sort((a,b) => a-b);
const area_cnt = area.length;
console.log(area_cnt);
console.log(sorted_area.join(" "));
